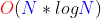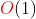【資料結構】堆排序
前言：
本章我們來講解八大排序之堆排序。2022，地球Online新賽季開始了！讓我們一起努力內卷吧！
一、堆排序的概念
📚 堆排序（Heapsort）：利用堆積樹（堆）這種資料結構所設計的一種排序演演算法，它是選擇排序的一種。通過堆來進行選擇資料，需要注意的是 排升序要建大堆，排降序建小堆。
堆排序使用堆來選數，效率就高了很多。
時間複雜度：
空間複雜度：
穩定性：不穩定
二、堆排序的實現
我們先建立一個堆排序的函數：
void HeapSort(int arr[], int n);假設我們要對下列陣列來使用堆排序（升序）：
int arr[] = {70, 56, 30, 25, 15, 10, 75};根據我們之前學到的知識，陣列是可以直接看作為完全二元樹的，所以我們可以把它化為堆。此時我們就可以 "選數" （堆排序本質上是一種選擇排序）。
第一步：構建堆
第一步就是要想辦法把 arr 陣列構建成堆（這裡我們先構建成小堆）。我們介紹兩種方法，分別為向上調整演演算法和向下調整演演算法：
方法1：向上調整
通過我們之前學過的 "向上調整" ，利用插入的思路來解決。首先設計下向上調整的演演算法：
void Swap(HPDataType* px, HPDataType* py) {
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}
/* 小堆的向上調整 */
void AdjustUp(int* arr, int child) {
assert(arr);
// 首先根據公式計算算出父親的下標
int parent = (child - 1) / 2;
// 最壞情況:調到根，child=parent 當child為根節點時結束（根節點永遠是0）
while(child > 0) {
if(arr[child] < arr[parent]) { // 如果孩子小於父親（不符合小堆的性質）
// 交換他們的值
Swap(&arr[child],&arr[parent]); // 傳地址
// 往上走
child = parent;
parent = (child - 1) / 2;
} else { // 如果孩子大於父親（符合小堆的性質）
// 跳出迴圈
break;
}
}
}① 首先，通過公式計算出父親的下標，公式如下：
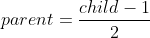
② 其次，設計迴圈部分，最壞情況為調到根，如果已經符合大堆的條件則終止迴圈。
③ 進入迴圈後進行判斷，如果 child ＞ parent，則交換它們的值，讓父親獲得孩子的值，孩子得到父親的值，從而讓它們符合大堆的性質。
④ 交換完畢後，以便於繼續判斷，我們需要更新 child 和 parent 指向的元素，做到 "往上走"
此時，我們把陣列裡的元素依次調整即可。
💬 方法1：
/* 升序 */
void HeapSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
AdjustUp(arr, i); // 傳入陣列 和 child的下標
}
}
我們不需要從 0 開始調，從 1 開始調。所以 i 的起始值設定為 1 。此時，小堆就構建好了。
方法2：向下調整
向下調整演演算法我們在堆那個章節也學過了，這裡我們再來複習一下：
void SmallAjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // 預設為左孩子
while(child < n) { // 葉子內
// 選出左右孩子中小的那一個
if(child + 1 < n && arr[child + 1] < arr[child]) {
child = child + 1;
}
// 如果孩子小於父親（不符合小堆的性質）
if(arr[child] < arr[parent]) {
// 交換它們的值
Swap(&arr[child], &arr[parent]);
// 往下走
parent = child;
child = parent * 2 + 1;
} else { // 如果孩子大於父親（符合小堆的性質）
// 跳出迴圈
break;
}
}
}① 因為要考慮左孩子還是右孩子，我們可以定義兩個變數，分別記錄左孩子和有孩子。但是我們這裡可以用更好的方法，只需要定義一個孩子即可。具體實現方法如下：首先建立 child，我們先預設它是左孩子，利用傳進來的 parent 根據公式計算出 child 的大小：
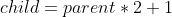
因為我們暫且預設為左孩子，我們隨後進入迴圈後要進行檢查，看看是左孩子大還是右孩子大，這裡我們只需要根據陣列的性質，將 child + 1 即可得到右孩子的下標，從而方便我們進行比較。比較完畢後將 child 重新賦值，拿個孩子小就將 child 給誰。
② 一共有兩個結束條件（出口），第一個結束條件是父親小於孩子就停止，第二個結束條件是chi調整到葉子。所以，迴圈體判斷部分根據我們分析的結束條件，如果調整到葉子就結束，我們接受了 n，也就是陣列的大小，只要 child 超過陣列的大小（child > n） 就結束，這是第一個出口。
③ 進入迴圈後，對比左孩子和右孩子哪一個更小，child 就交付給誰。這裡還要注意的是，要防止孩子不存在的情況，如果 child + 1 比 n 大，就說明孩子不存在。所以我們再寫 if 判斷條件的時候就要注意了，我們加一個 child + 1 < n 的條件限制一下：
if(child + 1 < n && arr[child + 1] < arr[child]) {...}④ 確認好較小的孩子後，我們就可以開始比較孩子和父親的大小了。如果孩子小於父親，就不符合小堆的性質，我們就要交換它們的值。這裡我們直接呼叫我們剛才寫的 Swap 介面即可，這就是為什麼在寫向上調整的時候要我們單獨把交換部分的程式碼寫成函數的原因。
⑤ 交換完畢後，他們的值已經互相交換好了，這時我們要改變 parent 和 child 的指向，讓它們往下走，parent = child ，child 再次根據公式算出新的 child 即可。
⑥ 設計下 if 的 else 部分，如果陣列的 child 的值大於 parent 的值，說明符合小堆的性質了， break 跳出迴圈即可，這是第二個出口。
向下調整演演算法的前提：左右子樹必須都是小堆
如果左子樹和右子樹不是小堆，怎麼辦？
可以用遞迴解決，但是我們能用迴圈就用迴圈來解決：
葉子所在的子樹是不需要調的。所以，我們從倒著走的第一個非葉子結點的子樹開始調。
（所以我們先調整30）
為了能夠演示得更明顯，我們再給陣列再加點資料，假設我們需要對以下陣列排序：
這裡，我們找到了15。
…… 下標不斷地 - - 後：
由於，從倒著走的第一個非葉子結點的子樹開始調，即，最後一個節點的父親。
我們已知最後一個節點的下標為：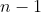 
那麼，我們可以通過公式計算出他父親的下標： ![parent = \frac{child -1}{2} \rightarrow \frac{\, \, \, [\, \, (n-1)-1\, \, ]\, \, \, }{2}](https://s3.ap-northeast-1.wasabisys.com/img.tw511.com/202201/gifogznhzhame5.gif)
💬 方法2：
/* 升序 */
void HeapSort(int arr[], int n) {
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(arr, n, i);
}
}⚡ 這麼寫或許可以看得更明白：
/* 升序 */
void HeapSort(int arr[], int sz) {
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
}🐞 測試堆是否建立好了：
我們這裡選擇使用方法2。此外，我們剛才實現的是小堆。
#include <stdio.h>
/* 交換函數 */
void Swap(int* px, int* py) {
int tmp = *px;
*px = *py;
*py = tmp;
}
/* 小堆下調 */
void AdjustDown(int arr[], int sz, int father_idx) {
int child_idx = father_idx * 2 + 1; // 計算出左孩子的值（預設認為左孩子大）
while (child_idx < sz) { // 最壞情況：調到葉子（child >= 陣列範圍時必然已經調到葉子）
if ((child_idx + 1 < sz) && (arr[child_idx + 1] < arr[child_idx])) { // 如果右孩子存在且右孩子比左孩子小
child_idx = child_idx + 1; // 讓其代表右孩子
}
if (arr[child_idx] < arr[father_idx]) { // 如果孩子的值小於父親的值（大符合小堆的性質）
Swap(&arr[child_idx], &arr[father_idx]); // 交換它們的值
/* 往下走 */
father_idx = child_idx; // 更新下標
child_idx = father_idx * 2 + 1; // 計算出該節點路線的新父親
} else { // 如果孩子的值大於父親的值（符合小堆的性質）
break; // 終止迴圈
}
}
}
/* 升序 */
void HeapSort(int arr[], int sz) {
/* 建立大堆，選出最大的數 O(N) */
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
}
void HeapPrint(int arr[], int sz) {
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main(void)
{
int arr[] = {70, 56, 30, 25, 15, 10, 75, 33, 50, 69};
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
HeapPrint(arr, sz);
return 0;
}🚩 執行結果：10 15 30 25 56 70 75 33 50 69
第二步：排序
剛才介紹了兩種方法來構建堆，現在堆已經構建完畢了，我們可以開始設計排序部分的演演算法了。
❓ 如果排升序，建小堆……
① 選出最小的數，放到第一個位置，這很簡單，直接取頂部就可以得到最小的數。
② 但問題來了，如何選出次小的數呢？
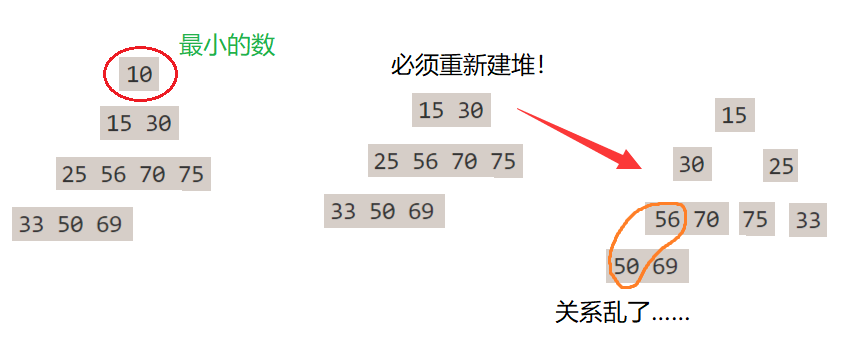
從 15 開始，剩下的元素看作一個堆。但是這之前建立好的堆關係全部亂了！你還得重新建堆，才能選出次小的數。建堆的時間複雜度為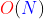 
，需要不斷地建堆 
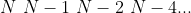則用小堆的時間複雜度就是 
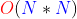，這太離譜了！搞了一大圈結果居然是 
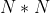，還不如直接遍歷選出來的方便呢。
建小堆來排升序是完全可以的，但是效率太低！完全沒有體現出你用堆的優勢！
⚡ 解決方法：使用大堆來排升序！
💬 我們剛才已經實現好小堆了，根據上一節學到的知識，小堆要變成大堆，直接把剛才的程式碼的 "<" 改成 ">" 即可：
#include <stdio.h>
/* 交換函數 */
void Swap(int* px, int* py) {
int tmp = *px;
*px = *py;
*py = tmp;
}
/* 大堆下調 */
void AdjustDown(int arr[], int sz, int father_idx) {
int child_idx = father_idx * 2 + 1; // 計算出左孩子的值（預設認為左孩子大）
while (child_idx < sz) { // 最壞情況：調到葉子（child >= 陣列範圍時必然已經調到葉子）
if ((child_idx + 1 < sz) && (arr[child_idx + 1] > arr[child_idx])) { // 如果右孩子存在且右孩子比左孩子大
child_idx = child_idx + 1; // 讓其代表右孩子
}
if (arr[child_idx] > arr[father_idx]) { // 如果孩子的值大於父親的值（不符合大堆的性質）
Swap(&arr[child_idx], &arr[father_idx]); // 交換它們的值
/* 往下走 */
father_idx = child_idx; // 更新下標
child_idx = father_idx * 2 + 1; // 計算出該節點路線的新父親
} else { // 如果孩子的值小於父親的值（符合大堆的性質）
break; // 終止迴圈
}
}
}
/* 升序 */
void HeapSort(int arr[], int sz) {
/* 建立大堆，選出最大的數 O(N) */
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
}
void PrintArray(int arr[], int sz) {
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main(void)
{
int arr[] = {70, 56, 30, 25, 15, 10, 75, 33, 50, 69};
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
PrintArray(arr, sz);
return 0;
}
🚩 執行結果：75 69 70 50 56 10 30 33 25 15
📚 現在改成了大堆，我們要排升序，我們可以讓堆頂數和最後的數進行交換：
這並不會帶來堆結構的破壞！我們把75不看作堆的一部分即可。再進行向下調整，就可以找到次小的數了。此時時間複雜度為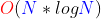 
🔺 步驟總結：
① 建大堆，選出最大的數。
② 最大的數跟最後一個數交換。
③ 如何選出次小的數呢？把最後一個數不看作堆裡面，進行向下調整。
💬 程式碼實現（用 while）：
/* 堆排序 - 升序 */
void HeapSort(int arr[], int sz) {
/* 建立大堆，選出最大的數 O(N) */
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
/* 依次選數，調堆 O(N * logN) */
int end = sz - 1;
while (end > 0) {
Swap(&arr[0], &arr[end]); // 最大的數跟最後一個數交換
AdjustDown(arr, end, 0); // 調堆，選出次小的數
end--;
}
}💬 程式碼實現（用 for）：
void HeapSort(int arr[], int sz) {
/* 建堆 */
for (int father = (sz - 1 - 1) / 2; father >= 0; father--) {
AdjustDown(arr, sz, father);
}
/* 排序 */
for (int end = sz - 1; end > 0; end--) {
Swap(&arr[0], &arr[end]); // 最大的數跟最後一個數交換
AdjustDown(arr, end, 0); // 調堆，選出次小的數
}
}三、完整程式碼
（排升序要建大堆，排降序建小堆）
💬 升序：使用大堆
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Swap(int* pa, int* pb) {
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
void AdjustDown(int arr[], int sz, int father) {
int child = father * 2 + 1;
while (child < sz) {
if (child + 1 < sz && arr[child + 1] > arr[child]) {
child += 1;
}
if (arr[child] > arr[father]) {
Swap(&arr[child], &arr[father]);
father = child;
child = father * 2 + 1;
}
else {
break;
}
}
}
/* 堆排序 - 升序 */
void HeapSort(int arr[], int sz) {
/* 建立大堆，選出最大的數 O(N) */
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
/* 依次選數，調堆 O(N * logN) */
int end = sz - 1;
while (end > 0) {
Swap(&arr[0], &arr[end]); // 最大的數跟最後一個數交換
AdjustDown(arr, end, 0); // 調堆，選出次小的數
end--;
}
}
void HeapPrint(int arr[], int sz) {
int i = 0;
for (i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main(void)
{
int arr[] = { 70, 56, 30, 25, 15, 10, 75, 33, 50, 69 };
int sz = sizeof(arr) / sizeof(arr[0]);
printf("排序前: ");
HeapPrint(arr, sz);
HeapSort(arr, sz);
printf("排序後: ");
HeapPrint(arr, sz);
return 0;
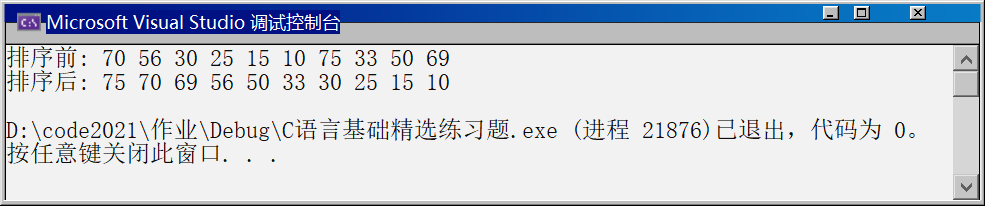
}🚩 執行結果：
❓ 如果要排降序呢？使用小堆即可！
💬 降序：使用小堆
#include <stdio.h>
/* 交換函數 */
void Swap(int* px, int* py) {
int tmp = *px;
*px = *py;
*py = tmp;
}
/* 小堆下調 */
void AdjustDown(int arr[], int sz, int father_idx) {
int child_idx = father_idx * 2 + 1; // 計算出左孩子的值（預設認為左孩子大）
while (child_idx < sz) { // 最壞情況：調到葉子（child >= 陣列範圍時必然已經調到葉子）
if ((child_idx + 1 < sz) && (arr[child_idx + 1] < arr[child_idx])) { // 如果右孩子存在且右孩子比左孩子小
child_idx = child_idx + 1; // 讓其代表右孩子
}
if (arr[child_idx] < arr[father_idx]) { // 如果孩子的值小於父親的值（不符合小堆的性質）
Swap(&arr[child_idx], &arr[father_idx]); // 交換它們的值
/* 往下走 */
father_idx = child_idx; // 更新下標
child_idx = father_idx * 2 + 1; // 計算出該節點路線的新父親
}
else { // 如果孩子的值大於父親的值（符合小堆的性質）
break; // 終止迴圈
}
}
}
/* 堆排序 - 降序 */
void HeapSort(int arr[], int sz) {
/* 建立大堆，選出最大的數 O(N) */
int father = ((sz - 1) - 1) / 2; // 計算出最後一個葉子節點的父親
while (father >= 0) {
AdjustDown(arr, sz, father);
father--;
}
/* 依次選數，調堆 O(N * logN) */
int end = sz - 1;
while (end > 0) {
Swap(&arr[0], &arr[end]); // 最大的數跟最後一個數交換
AdjustDown(arr, end, 0); // 調堆，選出次小的數
end--;
}
}
void PrintArray(int arr[], int sz) {
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main(void)
{
int arr[] = { 70, 56, 30, 25, 15, 10, 75, 33, 50, 69 };
int sz = sizeof(arr) / sizeof(arr[0]);
printf("排序前: ");
PrintArray(arr, sz);
HeapSort(arr, sz);
printf("排序後: ");
PrintArray(arr, sz);
return 0;
}🚩 執行結果：
四、證明建堆的時間複雜度
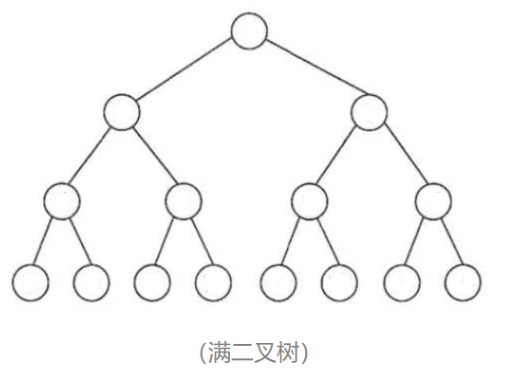
因為堆是完全二元樹，而滿二元樹也是完全二元樹。此處為了簡化，將採用滿二元樹來證明。（時間複雜度本來看的就是近似值，所以多幾個節點不會影響最終結果）：
假設樹的高度為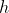 
：
第
層：
個節點，需要向下移動
層
第
層：
個節點，需要向下移動
層
第
層：
個節點，需要向下移動
層
第
層：
個節點，需要向下移動
層
……
第
層：
個節點，需要向下移動
則需要移動節點總的移動步數為：
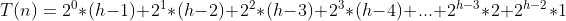①
②
② - ① 錯位相減：
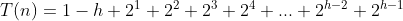
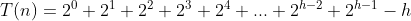
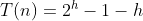
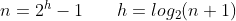
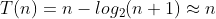
因此，建堆的時間複雜度為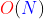
參考資料：
Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .
百度百科[EB/OL]. []. https://baike.baidu.com/.
📌 筆者：王亦優
📃 更新： 2021.11.26
❌ 勘誤： 無
📜 宣告： 由於作者水平有限，本文有錯誤和不準確之處在所難免，本人也很想知道這些錯誤，懇望讀者批評指正！
本篇完。