【玩轉二分查詢Ⅰ】左閉右閉型,左開右閉型,左閉右開型(動圖演繹)
目錄
一、前言
①什麼是二分查詢?
二分查詢是在有序表中查詢目標元素的演演算法,其基本思想其實就是「猜數位遊戲」——已知某個數k在0~1000之內,如何猜出這個數具體是多大呢?二分查詢是這樣處理的:
- k大於500嗎?不大於。所以我們將資料範圍壓縮到0~500之間
- k大於250嗎?大於。所以我們將資料範圍壓縮到250~500之間
- k大於375嗎?大於。所以我們將資料範圍壓縮到375~500之間
- ……
如此不斷的壓縮範圍資料的範圍,最後當只剩下1個資料時答案已經被鎖定了(當然如果運氣好,那我們選定的「折半值」可能就是k了),可以看到二分查詢不斷折半縮小待查詢的資料範圍因此二分查詢也被翻譯成「折半查詢」。
②二分查詢有多優秀?
試想如果我們從0~1000一一列舉,那我們最倒黴需要猜1000次,而使用二分的思路最壞也只 要需要10次(怎麼算出來的呢?![]() ,而
,而![]() ,所以10次就可以包含完0~1000的所有情況)。如果資料範圍更大些,那效率的差距將會更加的突出。
,所以10次就可以包含完0~1000的所有情況)。如果資料範圍更大些,那效率的差距將會更加的突出。
假設檢查一個元素需要1ms,那我們可以得到以下的表格:
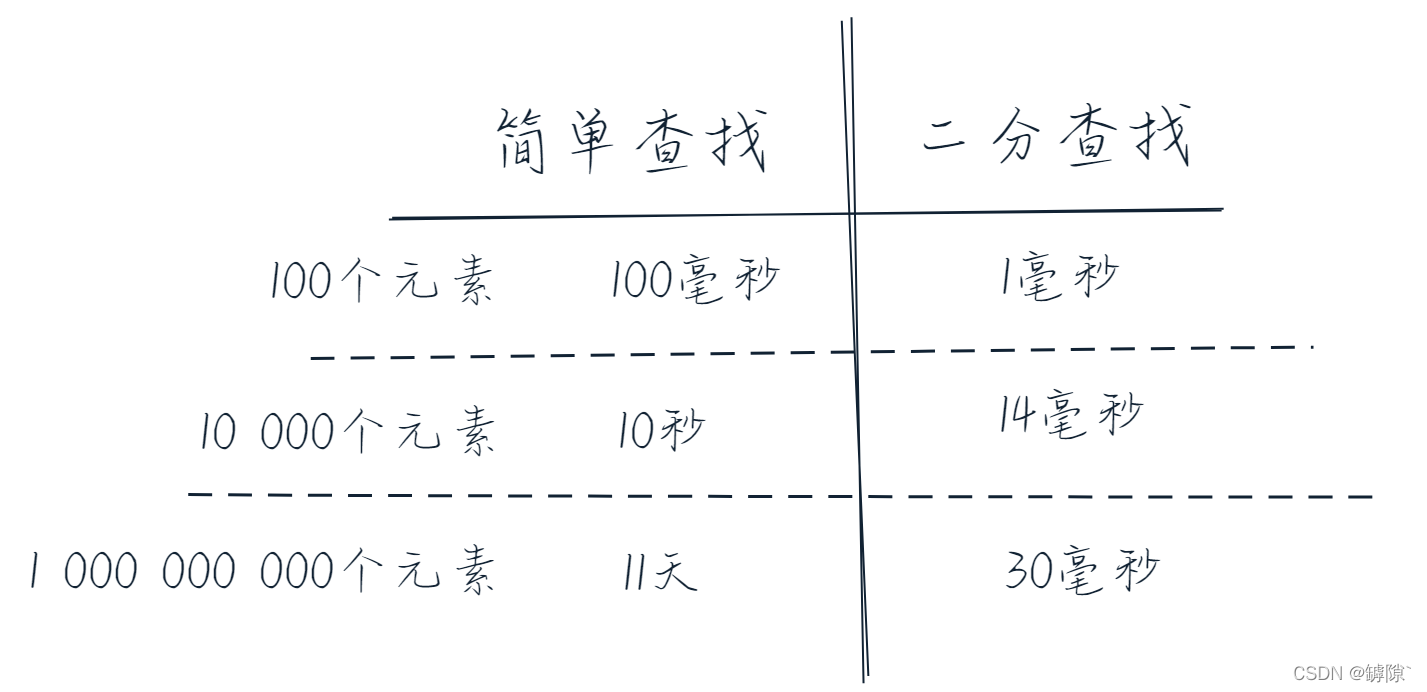
從這個實際問題中抽象出我們的演演算法,一一猜數對應著暴力列舉法,它的時間複雜度為![]() ,相比之下, 二分查詢的時間複雜度為
,相比之下, 二分查詢的時間複雜度為![]() ,所以是相當優秀漂亮的演演算法。
,所以是相當優秀漂亮的演演算法。
③使用前提
使用二分查詢的前提是原資料是一個有序表,即具有單調性。所以說檢索也是排序最重要的應用之一。
④二分查詢難嗎?
二分查詢真的很簡單嗎?其實也並不簡單。看看 Knuth 大佬(發明 KMP 演演算法的那位)怎麼說的:
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky...
這句話可以這樣理解:思路很簡單,細節是魔鬼。
所以在這篇文章中向大家介紹二分查詢的三種形式,雖然整體形式是極其相似的,但是略微的差別卻帶來了極大的不同。也相信學習完這篇部落格大家可以熟練運用這三種形式的二分查詢。
二、左閉右閉型
①程式碼模板
左閉右閉型是最典型的模板,也是我們學習的基礎,我們依然從猜數位的角度來理解:
int Binary_search(int*arr, int target, int numsSize)// (1)
{
int left = 0; //(2)
int right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) >> 1; //(3)
if (arr[mid] < target)
left = mid + 1; //(4)
else if (arr[mid] > target)
right = mid - 1;
else
return mid;
}
return -1; //(5)
}分析:
- (1)功能:查詢有序列表中target是否存在。存在則返回其下標,不存在則返回-1
- (2)left表示陣列下標範圍的下界,right表示陣列下標範圍的上界
- (3)求出中間值,也就是上面猜數位不斷的「折半」值,用它來界定我們的猜測小了還是大了
- (4)如果arr[mid] < target說明猜小了,所以將下界調整到mid+1
- (5)迴圈結束時left > right,說明遍歷了整個區間也找不到target,所以返回-1
看不懂?沒關係,用下面的四張動圖來幫你理解。
②動圖演示
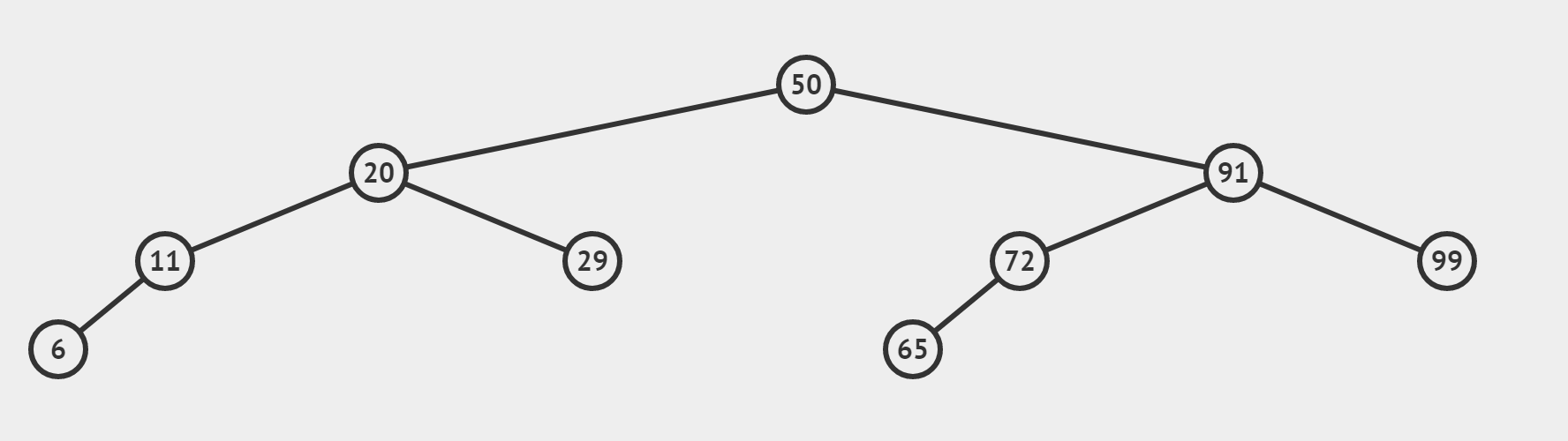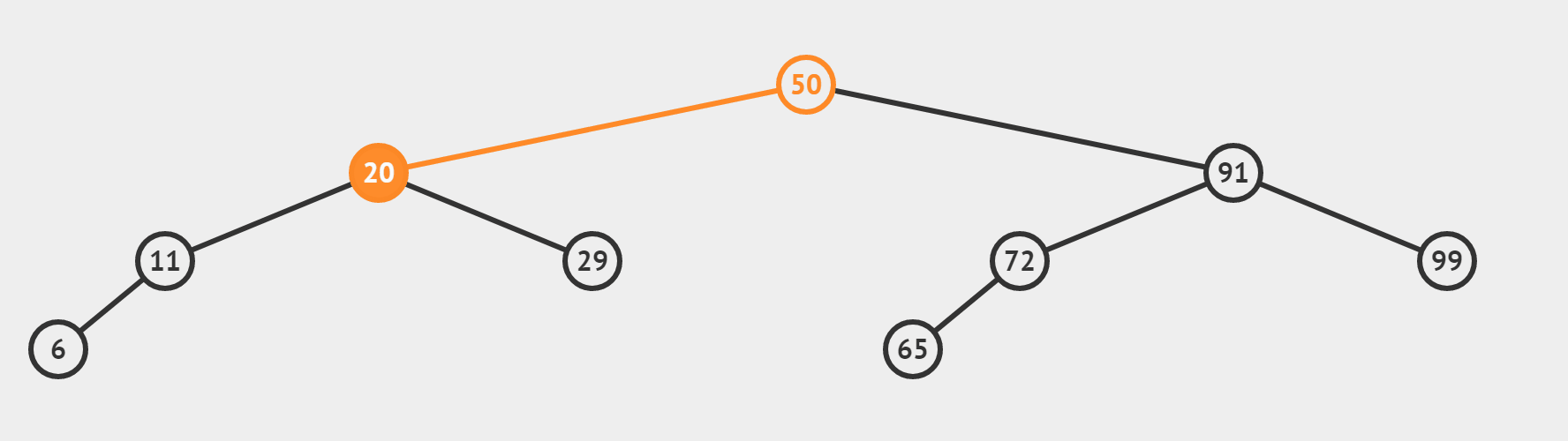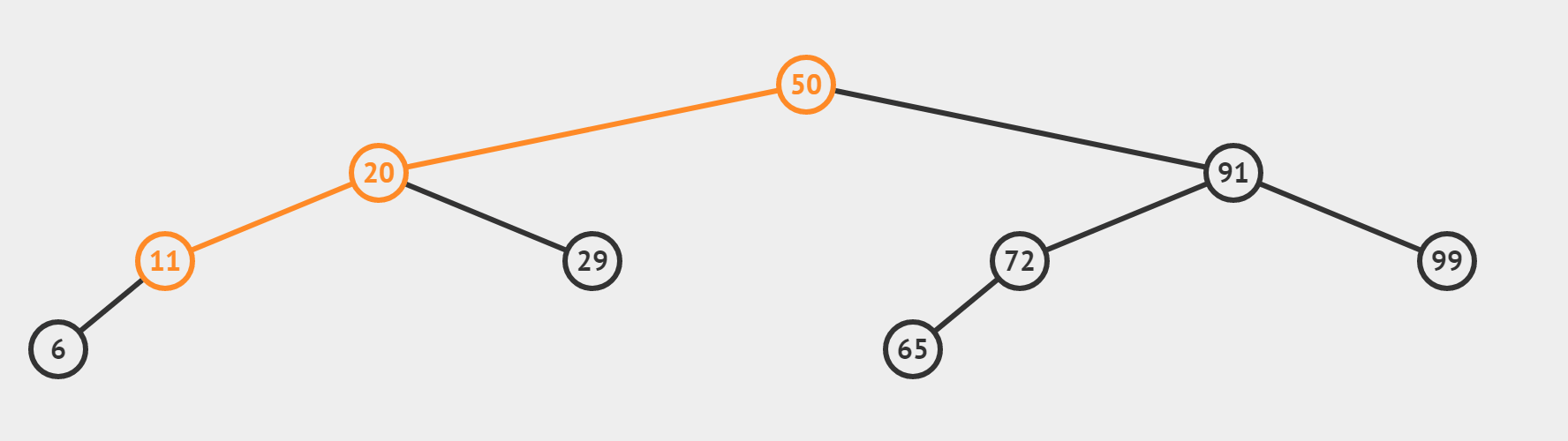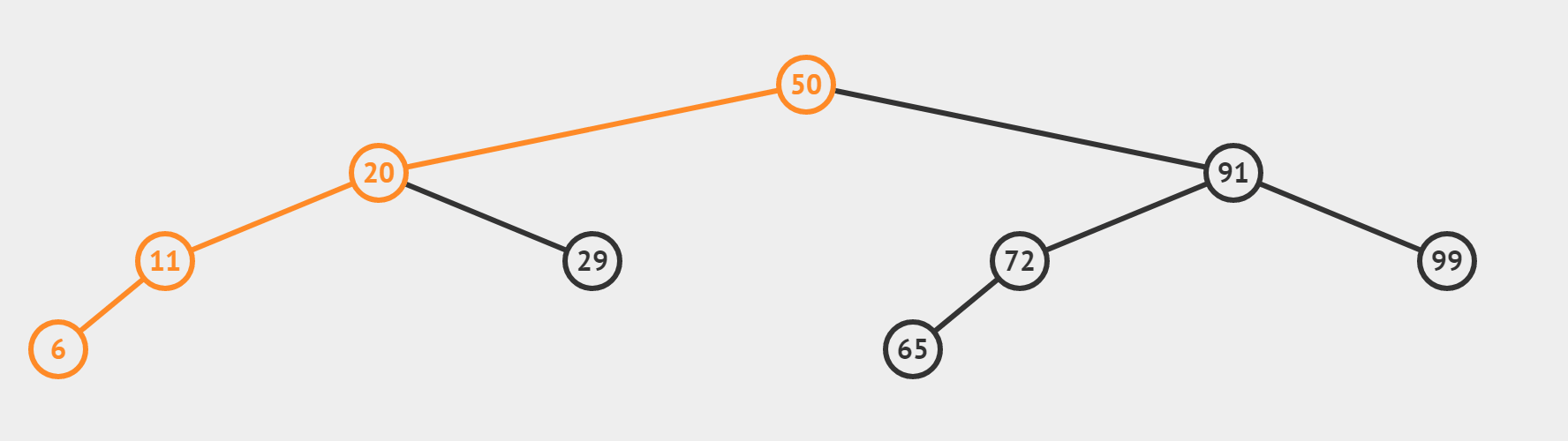
(1)檢索 target = 29 是否存在
更加直觀的,我們將資料資料對應到二元樹中
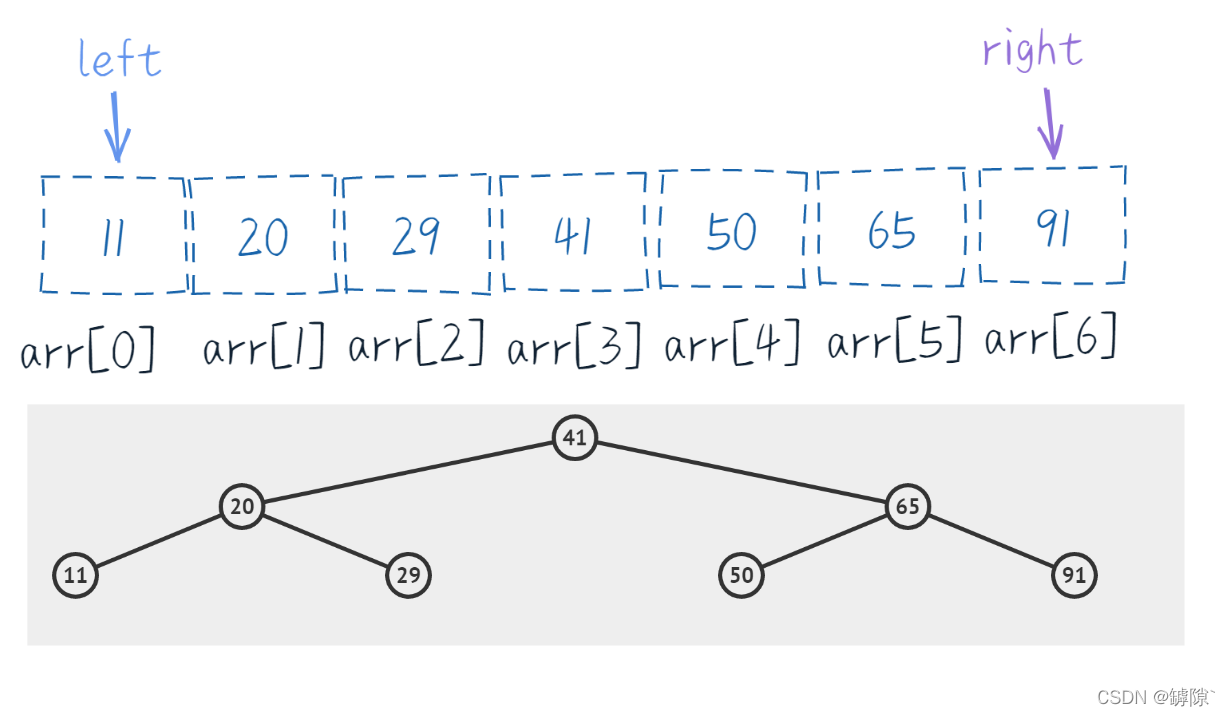
【如何構建的呢】
其實就是我們對猜數位遊戲的模擬,舉個🌰:
- 開始 left = 0, right = 6, mid = (left + right) / 2 = 3。由此我們建立出第一個結點41
- 如果target偏小,則 right = mid - 1 ,mid = (left + right) / 2 = 1.由此我們得到41的左子結點20
- 如果target偏大,則 left = mid + 1, mid = (left + right) / 2 = 5.由此我們得到41的右子結點65
- 同樣的道理我們對每個結點都分別求出其左右子結點(如果存在的話),就構造出二元樹了
【特性】
- 我們可以發現二元樹中元素自左向右依次遞增,即沒有改變原來的單調性
- 不難發現,遍歷到二元樹的最後一層時一定有 left = right = mid (三數合一)
- 若mid的計算髮生改成 (left + right + 1) / 2,構造出的二元樹的偏向會不同,讀者可自行嘗試
(2)檢索 target = 29 是否存在
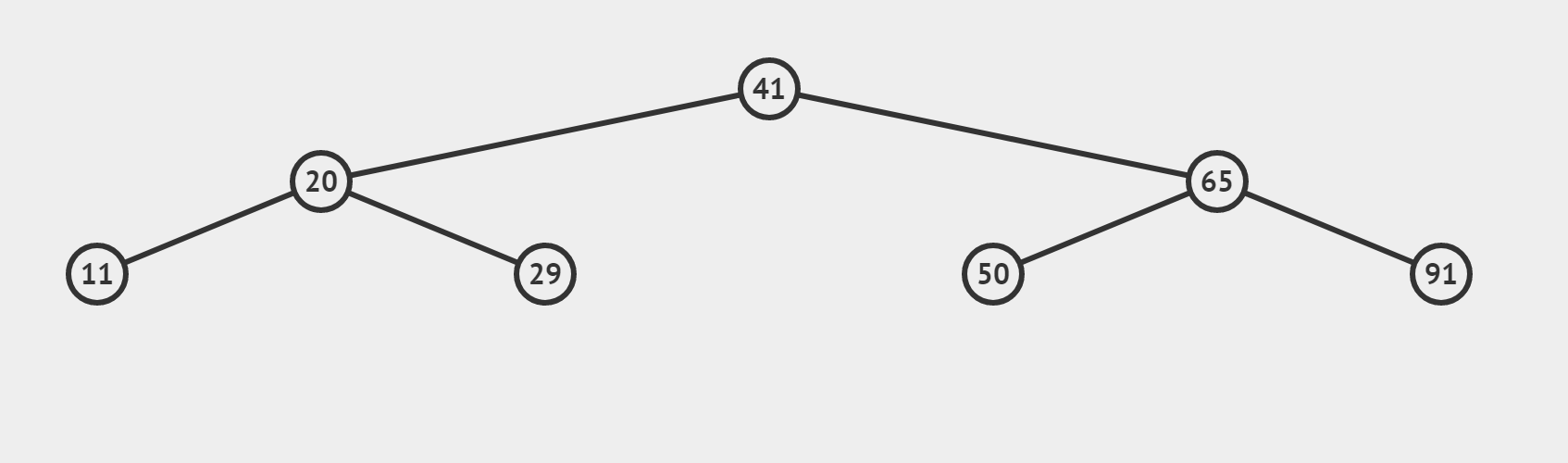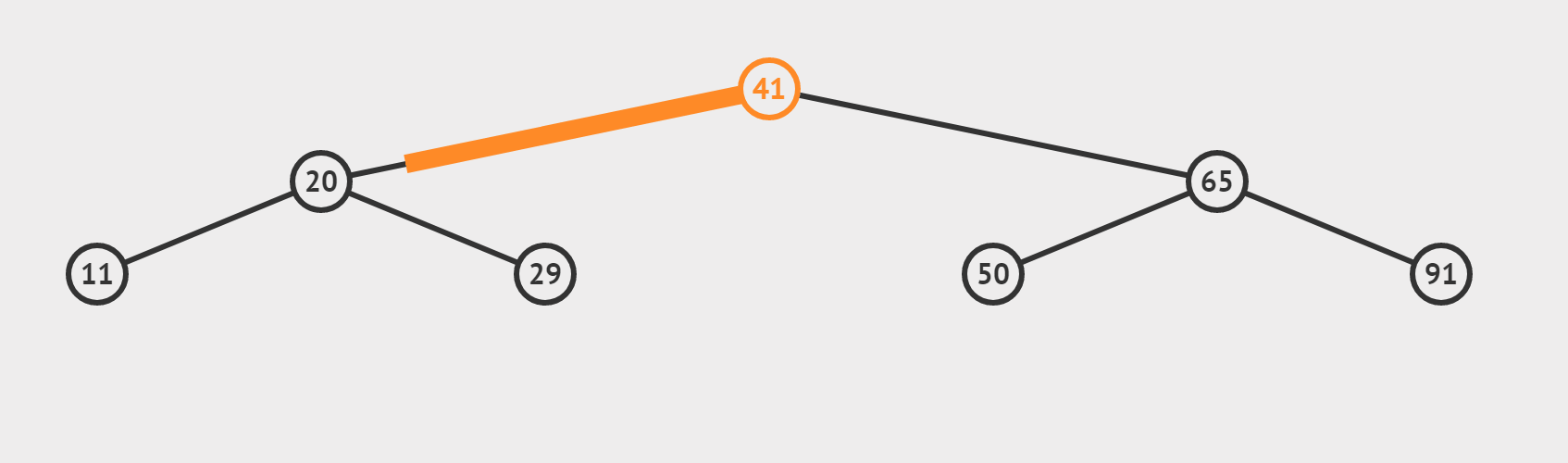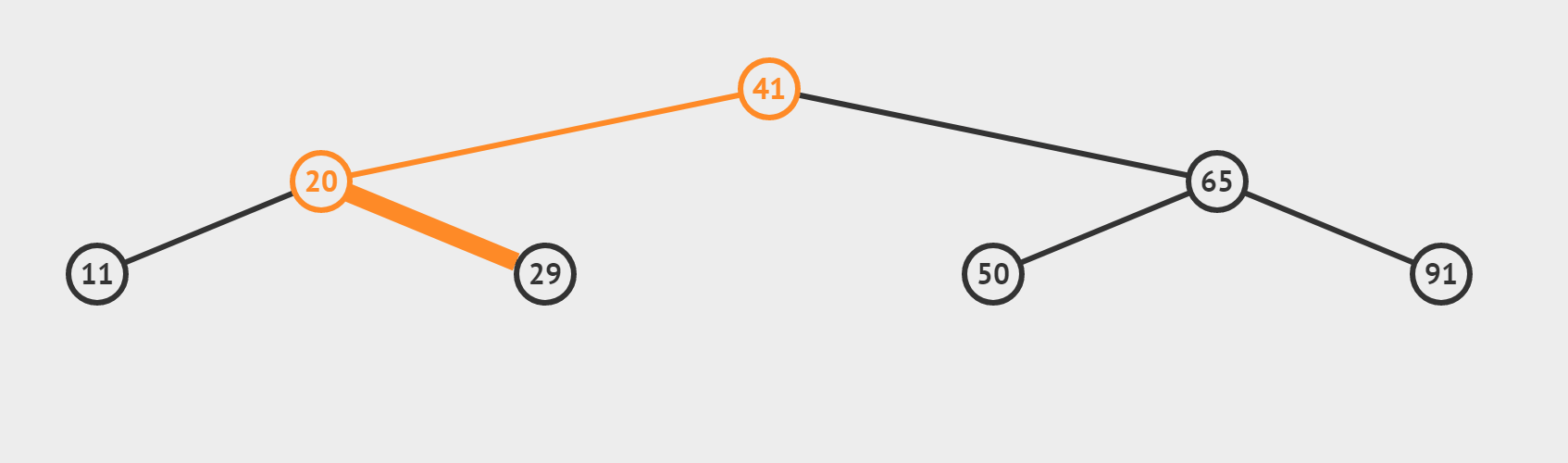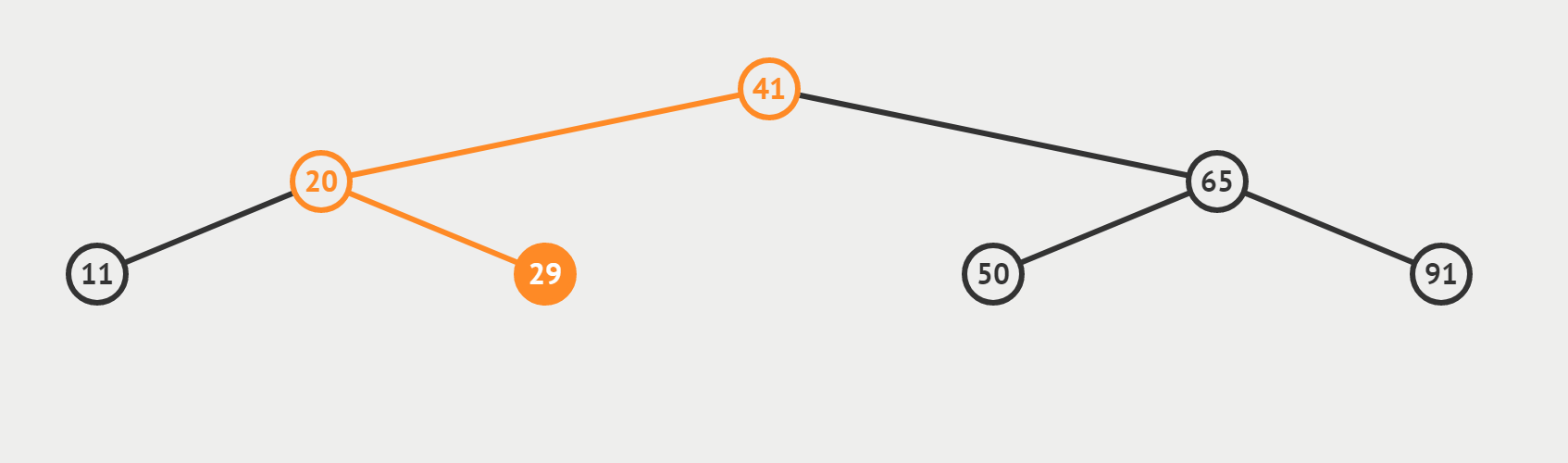
(3)target 找不到的情況(搜尋 target = 35)
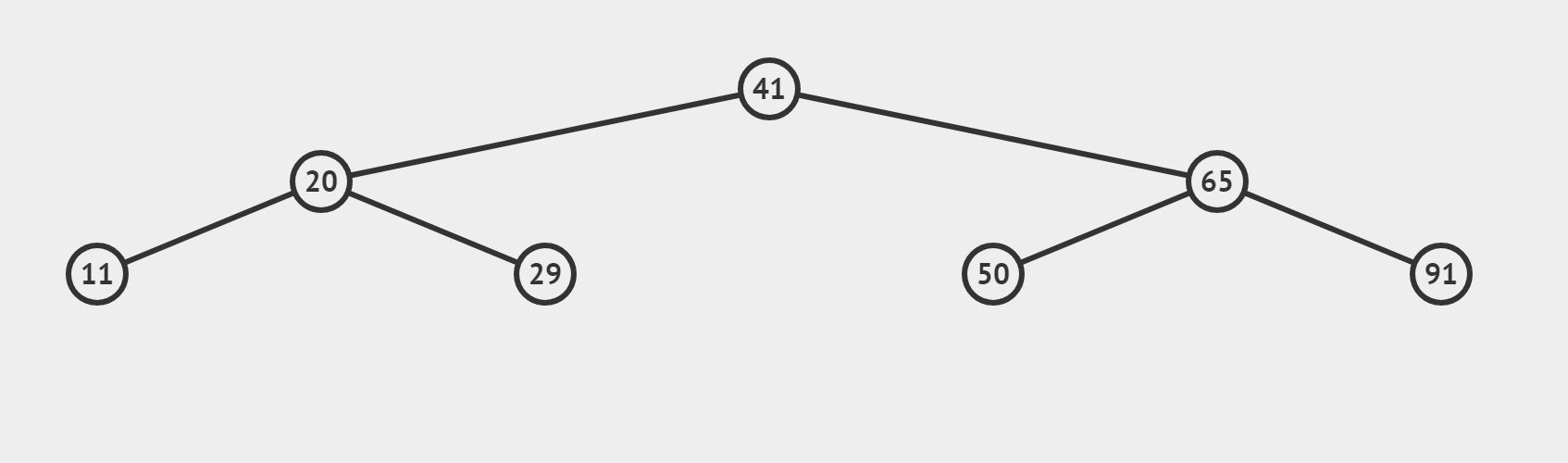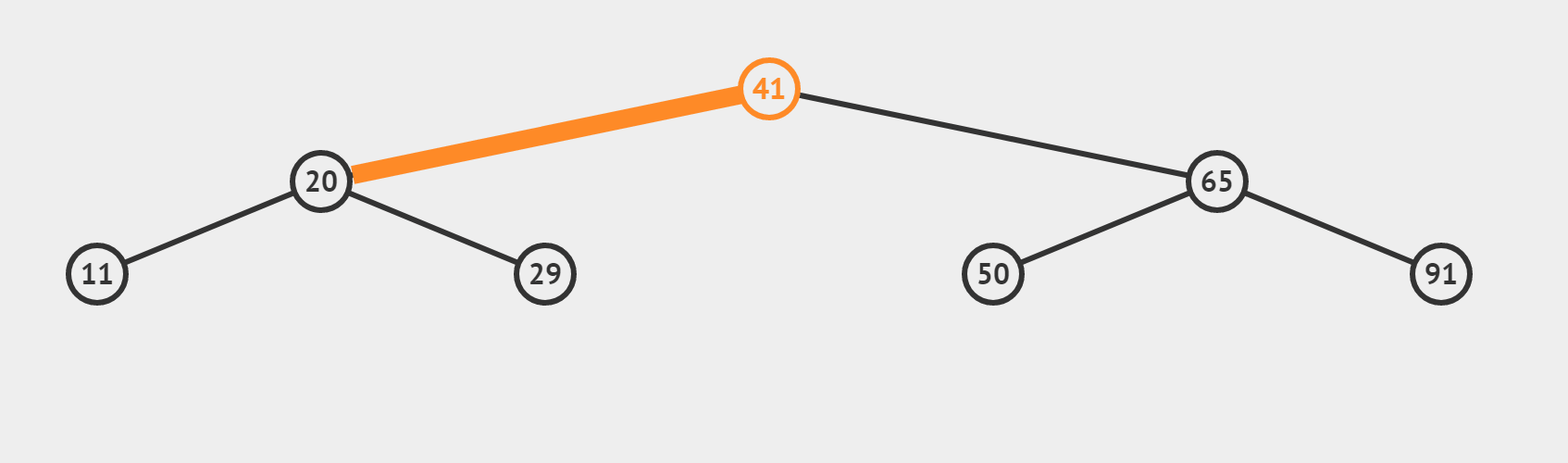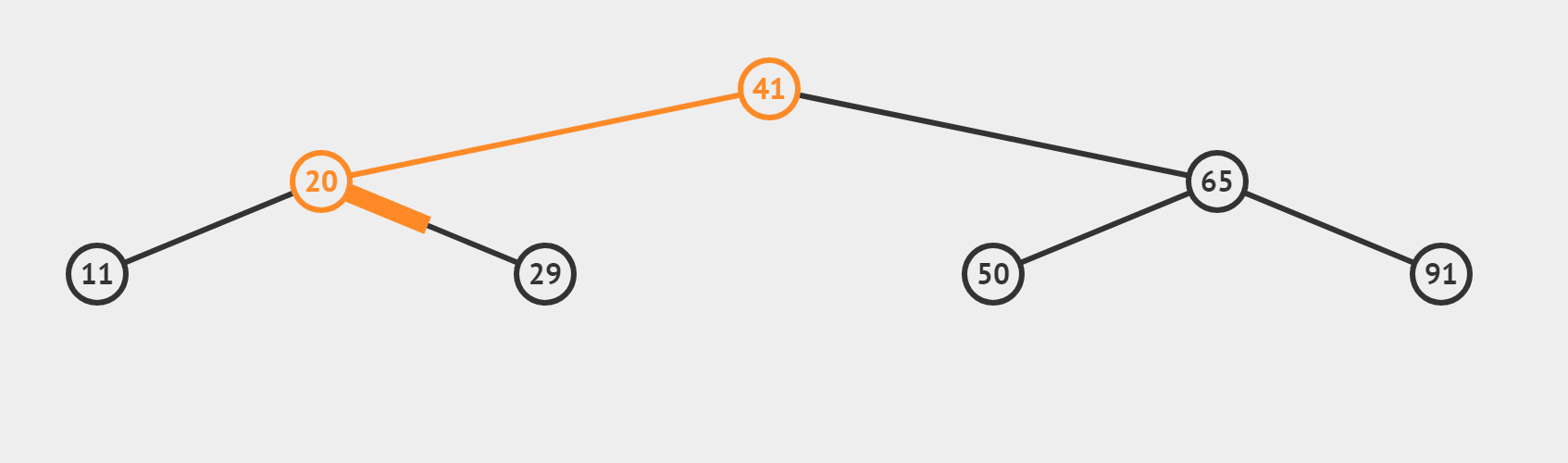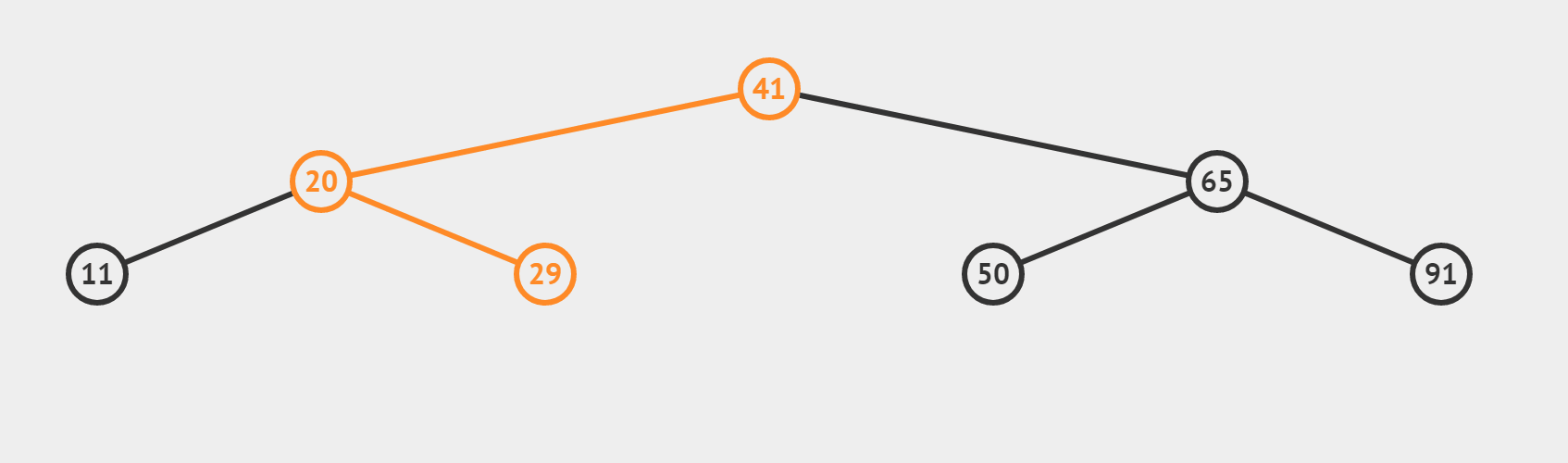
【和情況(2)有什麼區別呢】
- 若這個數是target,我們將直接返回它的下標,也即情況 (2)
- 若這個數不是我們的target,利用三數合一的結論,根據target偏大還是偏小,決定 left = mid + 1或者 right = mid-1 最終使得left > right,迴圈終止。所以相當於從最後一層向左或向右,「虛伸」出一條不存在的「小腿」。
(4)更復雜點的情況(採用mid = ( left + right + 1) / 2)
③中間位置取法的區別
以一組資料 [ 1, 2, 3, 4 , 5, 6 ]為🌰:
- mid = (left + right) / 2, 則獲得的mid = (0 + 5) / 2 = 2
- mid = (left + right + 1) / 2, 則獲得的mid = (0 + 5 + 1) / 2 = 3
- 兩種方法構造出的二元樹偏向不同,若某結點只有一個子結點,方法一得到的子節點一定是往右偏,方法二得到的一定是往左偏(如上圖的 6 , 65 都是往左偏的)
⭐[小細節]
如果left + right 存在溢位的問題,則上述中間位置的取法可以改成下面兩種形式,保證不會溢位
- (right - left) >> 1 + left
- (right - left + 1) >> 1 + left
④為什麼稱其為左閉右閉型
因為左閉右閉型檢索的區域在 [left , right] 之間。同樣的道理,左閉右開檢索的區域在 [left, right), 左開右閉的檢索區域在 (left, right]
三、左開右閉,左閉右開型
①左閉右開,左開右閉,左閉右開的區分
核心在於while判斷語句中有沒有等於號,以及中間值的取法。試想left 與 right不斷接近時,最終left 與right緊挨:
1) 中間值取法為 (left + right) / 2 時
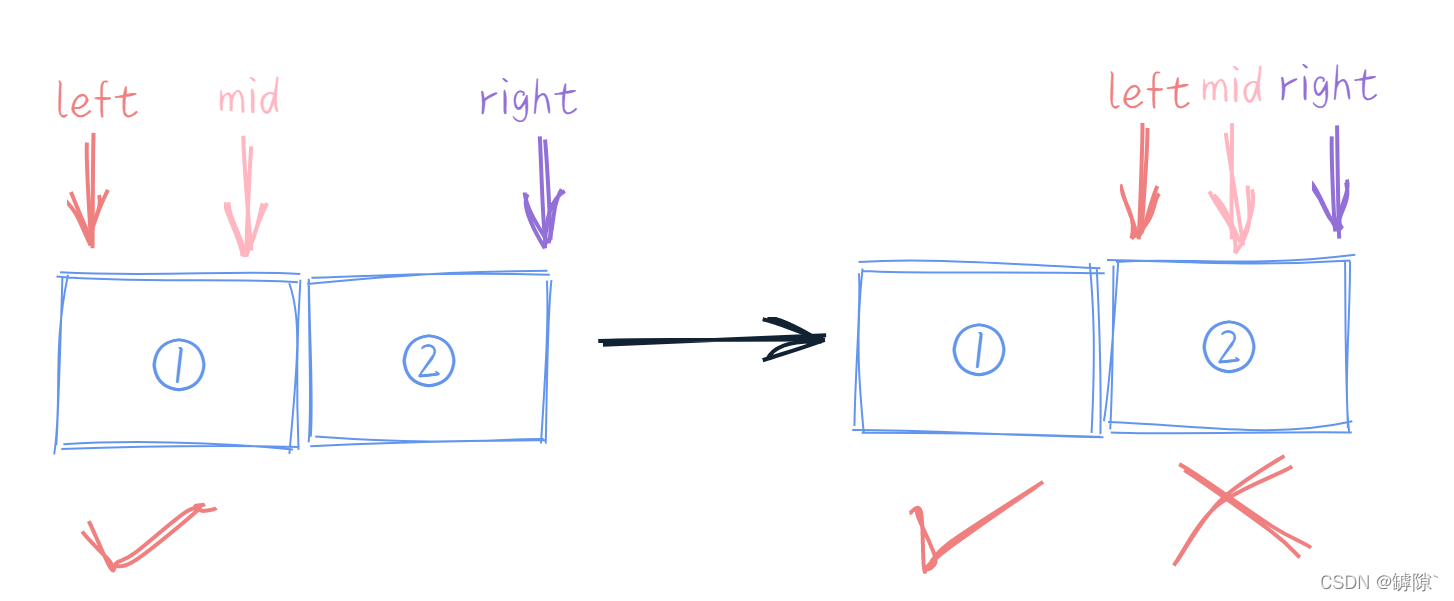
- 若判斷條件為 left <= right, 迴圈繼續,則點②也會被判斷,所以為左閉右閉
- 若判斷條件為 left < right, 迴圈結束, 則點②點不會被判斷,只有點①被檢索,所以稱為左閉右開(如上圖)
2)中間值取法為 (left + right + 1) / 2 時
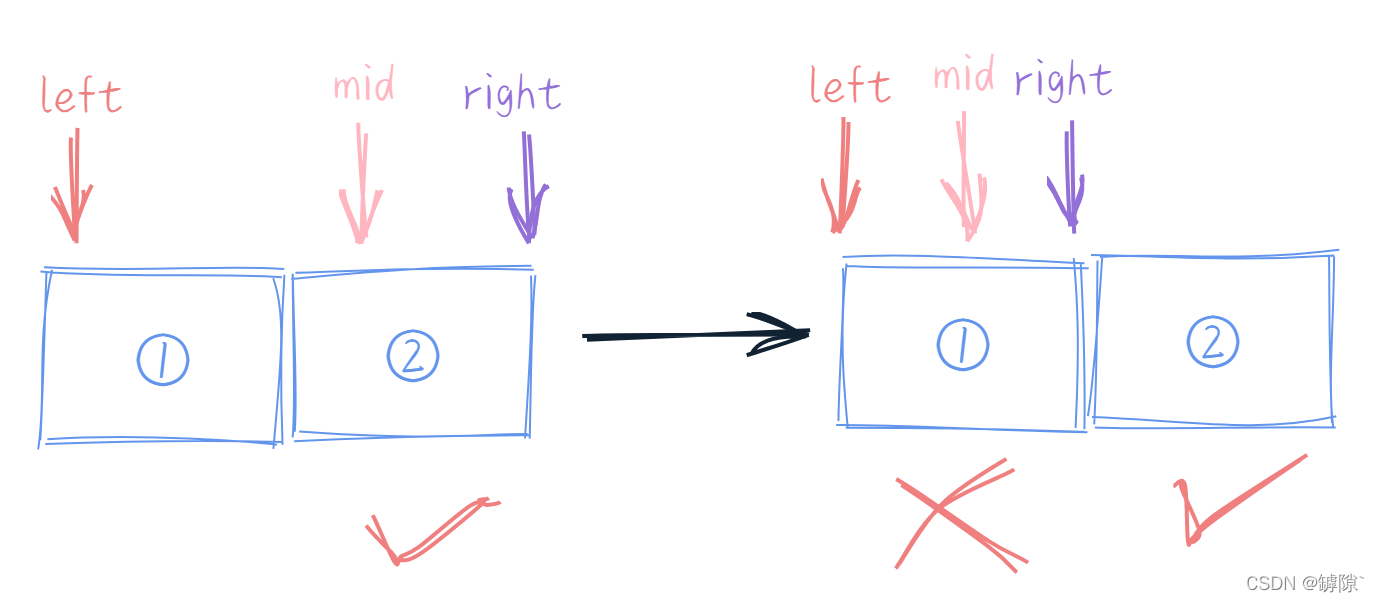
- 若判斷條件為 left <= right,則迴圈繼續,則點①也會被檢索,所以為左閉右閉
- 若判斷條件為 left < = right,則迴圈結束,則點①點不會被檢索,只有點②被檢索,所以稱為左開右閉(如上圖)
四、尋找上下界
二分查詢除了可以用來檢索一個數是否存在,還可以用來尋找上下界,來看看是怎樣實現的吧!
📃題目①:
假設你有n個版本[1, 2, ..., n],已知每個版本都是基於前一版本開發的。由於中間某一版本發生錯誤,導致之後的所有版本都是錯誤的。現需要你找出一個發生錯誤的版本。你可以呼叫函數bool isBadVersion(version)來檢測當前版本是否是錯誤版本(是錯誤版本返回1, 否則返回0)
int firstBadVersion(int n)
{
int left = 1;
int right = n;
while(left < right)
{
int mid = (right - left) / 2 + left;
if(isBadVersion(mid))
right = mid;
else
left = mid + 1;
}
return left;
}【分析】
1)為什麼想到二分查詢?
因為二分查詢的本質是二段性,只要滿足二段性的問題都可以轉化為二分查詢的問題。
2)如何理解二段性呢?
在猜數位遊戲中,二段性體現在target左邊的元素都比它小,target右邊的元素都比它大,所以結合資料的單調性我們可以不斷的壓縮區間以定位到目標值。而在這個問題中仍然具有二段性,第一個發生錯誤的版本的之前版本的都是正確的,之後的都是錯誤的,由此我們仍然可以不斷的壓縮區間從而得到第一個發生錯誤的版本。
3)如何理解左開右閉型的程式碼?
若當前mid版本為正確,則 left 可以壓縮到mid + 1,若當前版本正確,則將right壓縮到mid。可以是mid - 1嗎?不妨這樣思考,如果當前mid正處於第一個發生錯誤的版本,right = mid - 1後不是徹底排除了正確答案了嗎,永遠也找不到了。
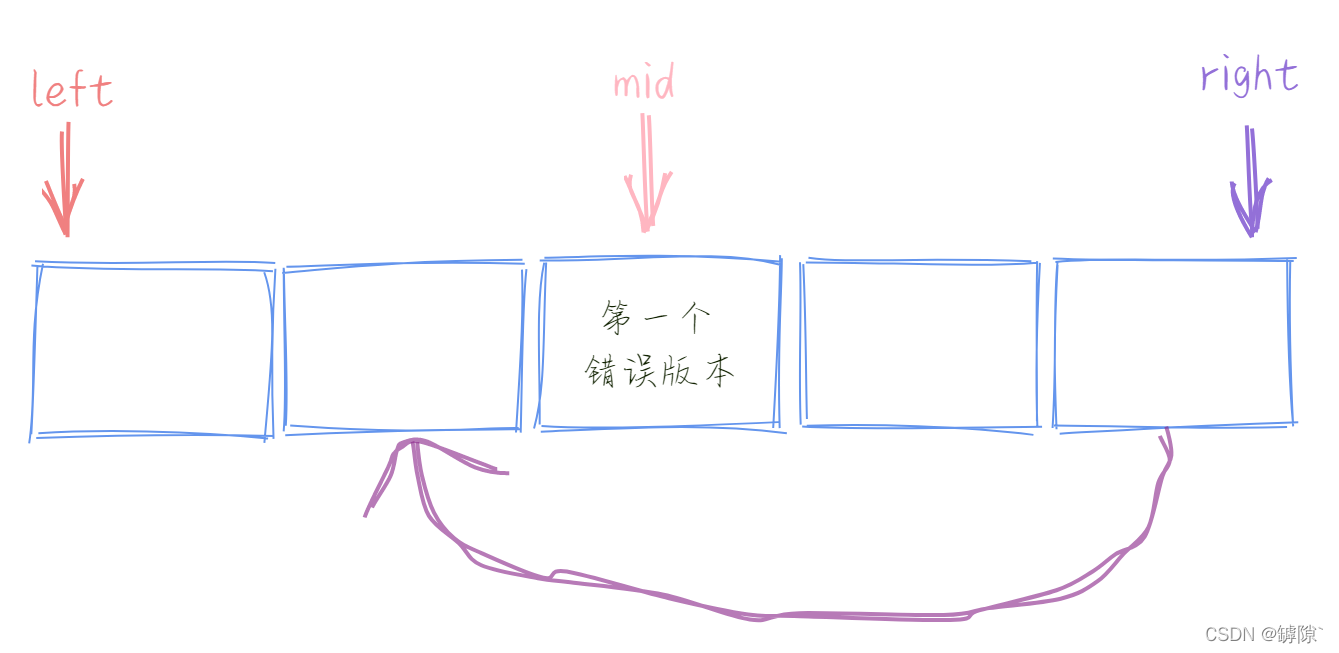
left 和 right 相遇之前,left不可能到達第一個錯誤版本,只會無限接近;right不可能超過第一個錯誤版本,只會到達第一個錯誤版本,所以最後 left 與 right 的關係是這樣的。最終, left = mid + 1使得 left 與 right重合也就鎖定了第一個錯誤版本 。
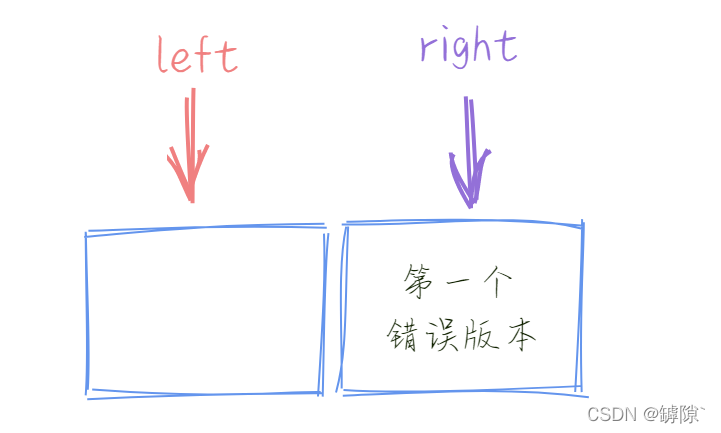
4)如果上體的中間元素取法為 (left + right + 1) / 2會發生什麼?
會陷入死迴圈! 因為 mid = right,mid是錯誤版本,因此執行語句"right = mid",也就意味著left 與 right的區間沒有發生壓縮。不斷重複這個過程就陷入了死迴圈。
5)延伸:如果最後的結果是這樣的呢?
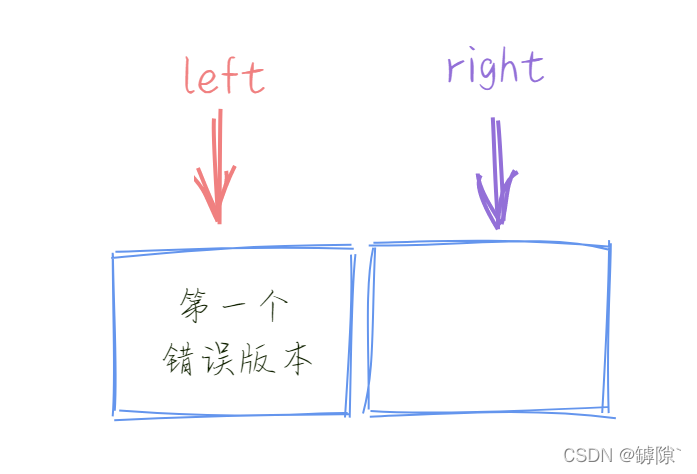
此時我們的中間元素取法如果為(left + right ) / 2 ,則同樣的我們會陷入死迴圈。
6)總結
- 左閉右開型的只可以用來尋找下界,左開右閉型的只可以用來尋找上界
- 根據題意明確好需要尋找上界還是下界後,我們就確定了中間元素的取法。對left,right怎麼處理呢?舉個例子,左閉右開型的左邊是取到到的,那麼加1的任務一定要交給它,保證不會陷入死迴圈。
📃題目②:
給定一個排序陣列和一個目標值,在陣列中找到目標值,並返回其索引。如果目標值不存在於陣列中,返回它將會被按順序插入的位置。
請必須使用時間複雜度為 O(log n) 的演演算法。
用左閉右閉型的二分查詢也可以實現上下界定位,並且好理解很多。來看看是怎麼實現的:
int searchInsert(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1, ans = numsSize;
while (left <= right)
{
int mid = ((right - left) >> 1) + left;
if (target <= nums[mid])
{
ans = mid;
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return ans;
}
【分析】與模板唯一的區別在於,找到了繼續找。所以上述程式碼的作用是找到第一個比target小的位置(也就是要插入位置)。當然如果將if裡的條件改成 " target >= nums[mid] ",那麼相應的作用就變成找到第一個閉target大的位置,當然也可以作為插入位置。
給大家演示一下: nums[] = {1, 2, 2, 2, 2, 2, 2, 3 ,4 ,5} , target = 2 的情況吧
五、鞏固練習
| 題目 | 地址 |
|---|---|
| 力扣地址 | |
| 力扣地址 | |
| 力扣地址 |
程式碼上面都呈現過,一定要都嘗試下。