智慧優化演演算法：野狗優化演演算法

摘要:野狗優化演演算法(Dingo Optimization Algorithm,DOA)是於2021年提出的一種新型智慧優化演演算法，該演演算法是根據澳大利亞野狗的社交行為設計的，具有尋優能力強，收斂速度快等特點。

1.演演算法原理

DOA演演算法的靈感來源於野狗的狩獵策略，即迫害攻擊、分組策略和清掃行為。

1.1 種群初始化

野狗種群在搜尋邊界內隨機初始化：
$$\overrightarrow{x_i}=l{b}_i+ran{d}_i(u{b}_i-l{b}_i)\text{\hspace{1em}(1)}$$
其中，$l{b}_i$和$u{b}_i$分別表示個體的上下邊界，$ran{d}_i$是[0,1]之間的亂數。

1.2 策略一：群體攻擊

捕食者通常使用高度智慧的狩獵技術，野狗通常單獨捕食小獵物，如兔子，但當捕食大獵物，如袋鼠時，它們會成群結隊。野狗能找到獵物的位置並將其包圍，其行為如式(2)所示：
$$\overrightarrow{x_i}(t+1)={\beta }_i\sum _{k=1}^{na}\frac{[\overrightarrow{{\phi }_k(t)-\stackrel{⃗}{x_i(t)}}]}{na}-\overrightarrow{x_{\ast }(t)}\text{\hspace{1em}(2)}$$
其中，$t$代表當前的迭代次數，$\overrightarrow{x_i}(t+1)$是野狗新位置；$na$是在$[2,SizePop/2]$的逆序中生成的隨機整數，其中$SizePop$是野狗種群的規模；$\overrightarrow{{\phi }_k(t)}$是將攻擊的野狗的子集，其中$\phi \in X$,是隨機生成的野狗種群；$\overrightarrow{x_i}(t)$是當前野狗的位置；$\overrightarrow{x_{\ast }}(t)$是上一次迭代中發現的最佳野狗；${\beta }_1$是在[-2,2]內均勻生成的亂數，它是一個比例因子，可改變野狗軌跡的大小。

1.3 策略二：迫害攻擊

野狗通常捕獵小獵物，直到單獨捕獲為止。式(3)模擬了這種行為：
$$\overrightarrow{x_i}(t+1)=\overrightarrow{x_{\ast }}(t)+{\beta }_1\ast e^{{\beta }_2}\ast (\overrightarrow{x_{r1}}(t)-\overrightarrow{x_i(t)})\text{\hspace{1em}(3)}$$
其中，$\overrightarrow{x_i}(t+1)$是野狗新位置，$\overrightarrow{x_{\ast }}(t)$是上一次迭代中發現的最佳野狗，${\beta }_1$的值與式(2)中的值相同，${\beta }_2$是在[-1,1]區間內均勻生成的亂數，$r_1$是在從1到最大搜尋代理(野狗)大小的區間內生成的亂數，$\overrightarrow{x_{r1}}(t)$是隨機選擇的第$r_1$個野狗，其中$i\ne r_1$。

1.4 策略三：清掃

清掃行為為被定義為當野狗在它們的棲息地隨意行走時找到腐肉吃的行為。式(4)用於模擬這種行為：
$$\overrightarrow{x_i}(t+1)=\frac{1}{2}[e^{{\beta }_2}\ast \overrightarrow{x_{r_1}}(t)-(-1{)}^{\sigma }\ast \overrightarrow{x_i}(t)]\text{\hspace{1em}(4)}$$
其中，$\overrightarrow{x_i}(t+1)$是野狗新位置，${\beta }_2$的值與式(3)中的值相同，$r_1$是在從1到最大搜尋代理(野狗)大小的區間內生成的亂數，$\overrightarrow{x_{r1}}(t)$是隨機選擇的第$r_1$個野狗，其中$i\ne r_1$。$\sigma$是演演算法隨機生成的二進位制數， σ ∈ { 0 , 1 } \sigma \in\{0,1\} σ∈{0,1}

1.5 策略四：野狗的存活率

在DOA中，野狗的存活率值由式(5)給出：
$$survial(i)=\frac{fitnes{s}_{max}-fitness(i)}{fitnes{s}_{max}-fitnes{s}_{min}}\text{\hspace{1em}(5)}$$
其中，$fitnes{s}_{max}$和$fitnes{s}_{min}$分別是當前一代中最差和最佳的適應度值，而$fitness(i)$是第$i$個野狗的當前適應度值。式(5)中的生存向量包含[0,1]區間內的歸一化適應度。式(6)通過策略三應用於低生存率，例如，生存率值等於或小於0.3。
$$\overrightarrow{x_i}(t+1)=\overrightarrow{x_{\ast }}(t)+\frac{1}{2}[\overrightarrow{x_{r_1}}(t)-(-1{)}^{\sigma }\ast \overrightarrow{x_{r2}}(t)]\text{\hspace{1em}(6)}$$
其中，$\overrightarrow{x_i}(t)$是將被更新的生存率較低的野狗，$r_1$和$r_2$是在從1到搜尋代理(野狗種群)的最大大小的區間內生成的亂數，$r_1\ne r_2$,$\overrightarrow{x_{r1}}$和$\overrightarrow{x_{r2}}$是隨機選擇的第$r1,r2$個野狗，$\overrightarrow{x_{\ast }}(t)$是上一次迭代中發現的最佳野狗；$\sigma$是演演算法隨機生成的二進位制數， σ ∈ { 0 , 1 } \sigma \in\{0,1\} σ∈{0,1}。

演演算法虛擬碼

procedure DOA
(2) Initialization of parameters
(3) P = 0.5, probability of hunting or scavenger strategy
(4) Q = 0.7, probability of Strategy 1 (group attack) or Strategy 2 (persecution attack)
(5) Generate the initial population
(6) while iteration < Max Number of Iterations do
(7) if random<P then
(8) if random<Q then
(9) Strategy 1: Group Attack Procedure, Algorithm 1, equation (2).
(10) else
(11) : Strategy 2: Persecution, (3).
(12) end if
(13) else
(14) Strategy 3: Scavenger, (4).
(15) end if
(16) Update search agents that have low survival value, Algorithm 3, equation (6)
(17) Calculate x new , the fitness value of the new search agents
(18) if x new <x ∗ then
(19) x ∗ = x new
(20) end if
(21) iteration = iteration + 1
(22) end while
(23) Display x ∗ , the best optimal solution

2.實驗結果

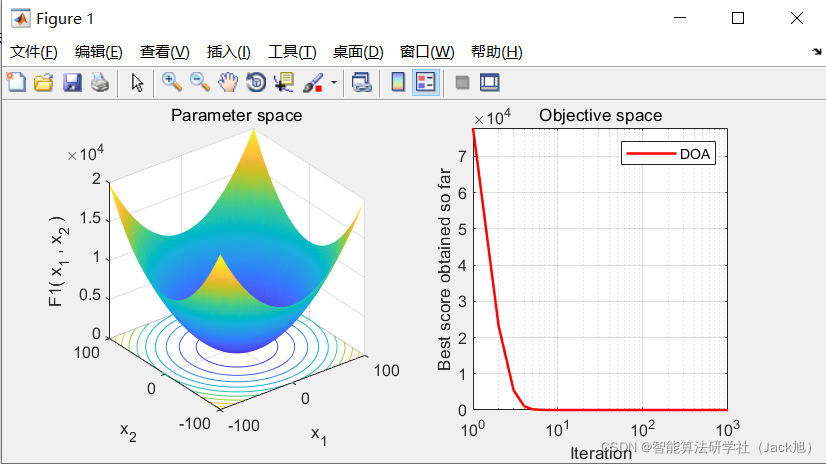
3.參考文獻

[1] Hernán Peraza-Vázquez, Adrián F. Peña-Delgado, Gustavo Echavarría-Castillo, et al. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies[J]. Mathematical Problems in Engineering, vol. 2021, Article ID 9107547, 19 pages, 2021.

4.Matlab程式碼