一維字首和

先看一個例子，假如我們現在有一個陣列

arr[]={3,2,5,6,7,8,9,4,2}

現在假如我們要想的得到區間 [ 3 , 6 ]，上的資料和，那我們就需要遍歷 [ 3 , 6 ] 這個區間進行求和。
程式碼如下：

#include <stdio.h>
int main()
{
	int arr[] = { 3,2,5,6,7,8,9,4,2 };
	int sum = 0;
	int l, r;
	scanf("%d%d", &l, &r);//獲取區間
	for (int i = l; i <= r; i++)
	{
		sum += arr[i];
	}
	printf("%d", sum);
	return 0;
}

假如我們需要多次詢問區間和時

#include <stdio.h>
int main()
{
	int arr[] = { 3,2,5,6,7,8,9,4,2 };
	int n = 0;
	scanf("%d", &n); //詢問次數
	for (int j = 0; j < n; j++)
	{
		int l, r;
		int sum = 0;
		scanf("%d%d", &l, &r);//獲取區間
		for (int i = l; i <= r; i++)
		{
			sum += arr[i];
		}
		printf("%d ", sum);
	}
	return 0;
}

它的時間複雜度將會是O(m*n)，當陣列很長，詢問次數很多時，這樣的求和方法效率就非常低下。
為了改進這種演演算法，就引入了字首和

字首和是指某序列的前n項和，可以把它理解為數學上的數列的前n項和，而差分可以看成字首和的逆運算。
合理的使用字首和與差分，可以將某些複雜的問題簡單化。

字首和公式

sum[i]=arr[i]          (i==0)
sum[i]=sum[i-1]+arr[i]  (i>0)

這個和高中的數列前n項和是差不多的
對於陣列

arr[]={3,2,5,6,7,8,9,4,2}

我們可以根據公式求出他的字首和陣列

sum[]={3,5,10,16,23,31,40,44,46}

當我們要詢問區間 [ l , r ] 上的數位和時

sum1=sum[r]-sum[l-1];

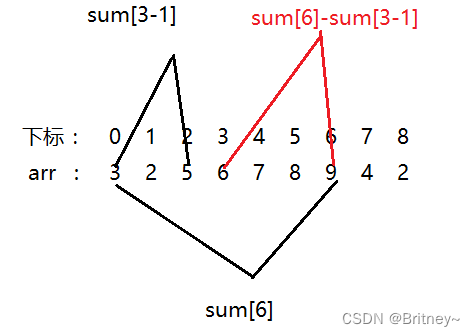
其實原理很好理解，比如我們我要求 [3 , 6 ] 上的區間和
sum[6]=arr[0]+arr[1]+arr[2]+arr[3]+arr[4]+arr[5]+arr[6]
sum[2]=arr[0]+arr[1]+arr[2];
sum[6]-sum[2]=arr[3]+arr[4]+arr[5]+arr[6]
如下圖所示·

程式碼如下：

#include <stdio.h>
#include<stdlib.h>
int main()
{
	int arr[] = { 3,2,5,6,7,8,9,4,2 };
	int m = sizeof(arr) / sizeof(arr[0]); //求元素個數
	int* sum = (int*)malloc(sizeof(int) * m);//開闢字首和陣列
	if (sum == NULL)  //判斷陣列是否開闢成功
		return 0;
	for (int i = 0; i < m; i++)
	{
		sum[i] = (i == 0) ? arr[i] : arr[i] + sum[i - 1];
	}
	int n = 0;
	scanf("%d", &n); //詢問次數
	for (int j = 0; j < n; j++)
	{
		int l, r;
		scanf("%d%d", &l, &r);//獲取區間
		printf("%d ", sum[r]-sum[l-1]);
	}
	return 0;
}

通過求字首和，我們可以把原本O(m*n)的時間複雜度化為O(n)

一維差分

還是剛剛的陣列

arr[]={3,2,5,6,7,8,9,4,2}

假如我們要對區間 [ 3 , 6 ] 上的資料都加上 m ，我們就需要遍歷這個區間。當我們需要多次進行如上操作時，
時間複雜度也將會成為O(m*n)
程式碼如下：

#include <stdio.h>
int main()
{
	int arr[] = { 3,2,5,6,7,8,9,4,2 };
	int n = 0;
	scanf("%d", &n);//獲取操作次數
	for (int i = 0; i < n; i++)
	{
		int l, r;
		scanf("%d%d", &l, &r);//獲取操作區間
		int p = 0;
		scanf("%d", &p);//獲取要加的數位大小
		for (int j = l; j <= r; j++)
		{
			arr[i] += p;
		}
	}
	return 0;
}

當陣列元素多，操作次數多時，這樣的程式碼也是十低效的。
這樣我們就需要引出差分了
差分陣列

sub[i]=arr[i]-arr[i-1]   (i!=0)
sub[i]=arr[i]            (i==0)

對上面的陣列求差分可以得到

sub[]={3,-1,3,1,1,1,1,-5,-2}；

差分陣列的性質
1.對差分陣列進行字首和，就可以的到原陣列
分析：

原陣列：  a1       a2        a3       a4       a5
差分陣列：a1      a2-a1     a3-a2    a4-a3    a5-a4
字首和：  a1       a2        a3       a4       a5

2.要對陣列區間 [ l, r ] 的資料都加上m時，我們只需要對差分陣列的

sub[l]+=m;
sub[r+1]-=m;

即可，所有操作做完後，做字首和求出原陣列即可
注意事項：如果r+1可以超過原陣列大小，所以我們可以在開闢sub陣列時多開闢一塊空間，也可以對超過原陣列的情況不做任何處理（不求差分），也是不會影響結果的。
程式碼如下：

#include <stdio.h>
#include<stdlib.h>
int main()
{
	int arr[] = { 3,2,5,6,7,8,9,4,2 };
	int m = sizeof(arr) / sizeof(arr[0]);//求陣列大小
	int* sub=(int*)malloc(sizeof(int) * (m+1));
	if (sub == 0)
		return 0;//判斷是否開闢成功
	for (int i = 0; i <= m; i++)
	{
		sub[i] = (i == 0) ? arr[i] : arr[i] - arr[i - 1];
	}
	int n = 0;
	scanf("%d", &n);//獲取操作次數
	for (int i = 0; i < n; i++)
	{
		int l, r;
		scanf("%d%d", &l, &r);
		int p = 0;     //
		scanf("%d", &p);//獲取要加的數
		sub[l] += p;
		sub[r + 1] -= p;
	}
	//恢復陣列
	for (int i = 0; i < m; i++)
	{
		arr[i] = (i == 0) ? sub[i] : sub[i] + arr[i - 1];
	}

	return 0;
}

二維字首和

上面我們討論了一維陣列，但二維陣列我們需要怎樣處理呢？
如下陣列：

	int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };

如下圖：

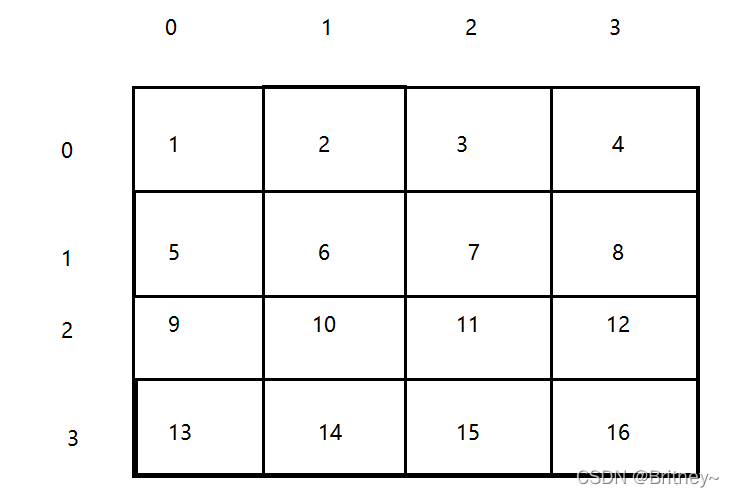
如過我們要求（1，1）到 （2，2）的陣列和
也就是

也就是上圖中紅色框中和
當我們要多次詢問的話，按普通演演算法來算的化時間複雜度是O(m*n)
程式碼如下

#include <stdio.h>
#include<stdlib.h>
int main()
{
	int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };
	int n = 0;
	scanf("%d", &n);//獲取操作次數
	for (int i = 0; i < n; i++)
	{
		int x1, y1, x2, y2;
		scanf("%d%d",& x1, &y1);
		scanf("%d%d",& x2, &y2);
		int sum = 0;
		for (int p = x1; p <= x2; p++)
		{
			for (int q = y1; q <= y2; q++)
			{
				sum += arr[p][q];
			}
		}
		printf("%d ", sum);
	}


	return 0;

這種演演算法是很低效的，為了提高效率，我們可以先求出二位字首和陣列

sum[i][j]是從（0，0）到（i，j）的和

具體方法如下：

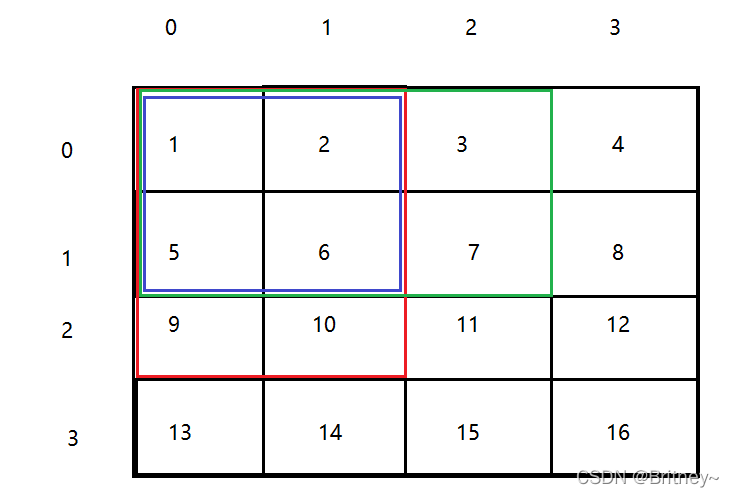
如有要求

sum[2][2]

就可以

sum[2][2]=sum[1][2]+sum[2][1]+arr[2][2]-sum[1][1];

結合圖還是很好理解的
總結如下：
當 i!=0,j!=0;時

sum[i][j]=sum[i-1][j]+sum[i][j-1]+arr[i][j]-sum[i-1][j-1];

當i==0，j!=0;時

sum[0][j]=sum[0][j-1]+arr[0][j];

當j==0,i!=0時

sum[i][0]=sum[i-1][0]+arr[i][0];

當i== 0, j==0時

sum[0][0]=arr[0][0];

程式碼如下：

int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };
	int a = 4, b = 4;
	int** sum = (int**)malloc(sizeof(int*) * a);
	for (int i = 0; i < a; i++)
	{
		sum[i] = (int*)malloc(sizeof(int) * b);
		for (int j = 0; j < b; j++)
		{
			if (i == 0 && j == 0)
				sum[0][0] = arr[0][0];
			else if (i != 0 && j == 0)
				sum[i][0] = sum[i - 1][0] + arr[i][0];
			else if (i == 0 && j != 0)
				sum[0][j] = sum[0][j - 1] + arr[0][j];
			else
				sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + arr[i][j] - sum[i - 1][j - 1];
		}
	}

當我們有了字首和陣列後，解決最開始的問題就簡單多了
如果要求（1，1）到（2，2）的和

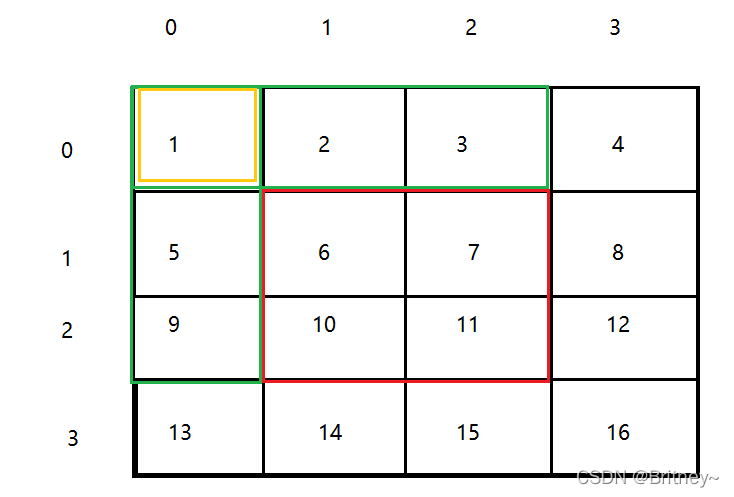
sum2=sum[2][2]-sum[2][0]-sum[0][2]+sum[0][0]

總結如下：
（x1,y1）,(x2,y2), 前提是 (x1<=x2,y1<=y2)
x1== 0&&y1==0

sum2=sum[x2][y2]

x1!=0&&y1==0

sum2=sum[x2][y2]-sum[x1-1][y2];

x1==0&y1!=0

sum2=sum[x2][y2]-sum[x2][y1-1]

x1!=0&&y1!=0

sum2=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y2-1];

完整程式碼：

#include <stdio.h>
#include<stdlib.h>
int main()
{
	int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };
	int a = 4, b = 4;
	int** sum = (int**)malloc(sizeof(int*) * a);
	for (int i = 0; i < a; i++)
	{
		sum[i] = (int*)malloc(sizeof(int) * b);
		for (int j = 0; j < b; j++)
		{
			if (i == 0 && j == 0)
				sum[0][0] = arr[0][0];
			else if (i != 0 && j == 0)
				sum[i][0] = sum[i - 1][0] + arr[i][0];
			else if (i == 0 && j != 0)
				sum[0][j] = sum[0][j - 1] + arr[0][j];
			else
				sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + arr[i][j] - sum[i - 1][j - 1];
		}
	}
	int n = 0;
	scanf("%d", &n);//獲取操作次數
	for (int i = 0; i < n; i++)
	{
		int x1, y1, x2, y2;
		scanf("%d%d",& x1, &y1);
		scanf("%d%d",& x2, &y2);
		int sum2 = 0;
		if (!x1 && !x2)
			sum2 = sum[x2][y2];
		else if (!x1)
			sum2 = sum[x2][y2] - sum[x2][y1 - 1];
		else if (!y1)
			sum2 = sum[x2][y2] - sum[x1 - 1][y2];
		else
			sum2 = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
		printf("%d ", sum2);
	}
	return 0;
}

二維差分

同理還是上面陣列

int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };

假如我們想要把（1，1）到（2，2）這個區間都加上數位m，用原始的演演算法也是很慢的，為了加快效率，也是可以用的，也是可以用到差分的，也就是二維差分。

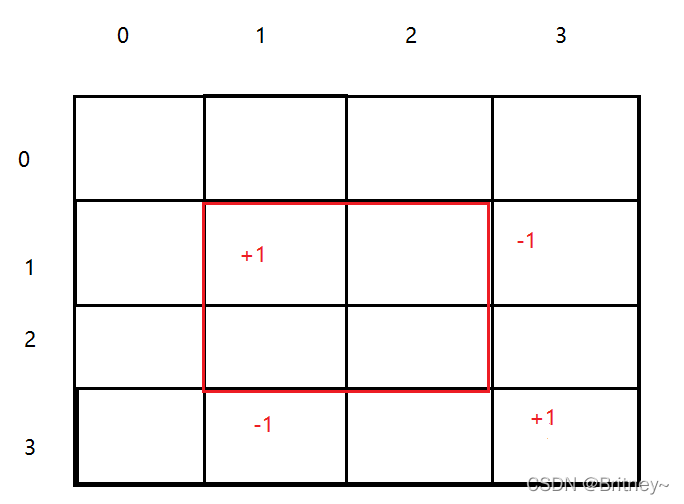
我們只需要對差分陣列

sub[1][1]+=m
sub[3][1]-=m
sub[1][3]-=m
sub[3][3]+=m

總結：要在區間（x1,y1）到(x2,y2)都加上m

sub[x1][y1]+=m;
sub[x1][y2+1]-=m;
sub[x2+1][y1]-=m;
sub[x2+1][y2+1]+=m;

程式碼：

#include <stdio.h>
#include<stdlib.h>
int main()
{
	int arr[][4] = { {1 ,2, 3, 4},
					 {5, 6, 7, 8},
					 {9, 10, 11,12},
					 {13,14,15, 16} };
	int a = 4, b = 4;
	int n = 0;
	scanf("%d", &n);//獲取操作次數
	int** sub = (int**)calloc(a+1,sizeof(int*));
	for (int i = 0; i < a+1; i++)
	{
		sub[i] = (int*)calloc(b + 1, sizeof(int));   //先把陣列開闢出來
	}
	for (int p = 0; p < n; p++)    //求差分陣列
	{
		int x1, y1, x2, y2;
		scanf("%d%d", &x1, &y1);    
		scanf("%d%d", &x2, &y2);      //獲取操作區間
		int m = 0;                  //要加的數位大小
		scanf("%d", &m);
		sub[x1][y1] += m;
		sub[x2 + 1][y2 + 1] += m;
		sub[x1][y2 + 1] -= m;
		sub[x2 + 1][y1] -= m;
	}
	//對差分陣列求字首和
	for (int i = 0; i < a; i++)
	{
		for (int j = 0; j < b; j++)
		{
			if (i == 0 && j == 0)
				sub[0][0] = sub[0][0];
			else if (i != 0 && j == 0)
				sub[i][0] = sub[i - 1][0] + sub[i][0];
			else if (i == 0 && j != 0)
				sub[0][j] = sub[0][j - 1] + sub[0][j];
			else
				sub[i][j] = sub[i - 1][j] + sub[i][j - 1] + sub[i][j] - sub[i - 1][j - 1];
		}
	}
	//對映回原陣列
	for (int i = 0; i < a; i++)
	{
		for (int j = 0; j < b; j++)
		{
			arr[i][j] += sub[i][j];
		}
	}
	return 0;
}