【NLP】再看交叉熵損失函數
交叉熵
在深度學習領域出現交叉熵(cross entropy)的地方就是交叉熵損失函數了。通過交叉熵來衡量目標與預測值之間的差距。瞭解交叉熵還需要從資訊理論中的幾個概念說起。
資訊量
如何衡量一條資訊包含的資訊量?加入我們有以下的兩個事件:
事件1:年底昆明要下雪
事件2:年底哈爾濱要下雪
憑直覺來說,事件1的資訊量比事件2的資訊量大,因為昆明一年四季如春,下雪的機率非常小。所以當越不可能的事件發生了,我們獲取到的資訊量就越大。越可能發生的事件發生了,我們獲取到的資訊量就越小,這也是香濃資訊理論中的一部分。資訊量的定義就與事件發生的概率有關。
將其數學化。概率的取值範圍是
[
0
,
1
]
[0, 1]
[0,1],並且滿足值越大資訊量越小的走勢,資訊量的取值範圍是
(
0
,
+
∞
)
(0, +\infty)
(0,+∞),假設事件
x
x
x發生的概率為
p
(
x
)
p(x)
p(x),在數學上我們選取負對數來表示一個事件的資訊量,如下:
I
(
x
)
=
−
log
(
p
(
x
)
)
I(x) = - \log (p(x))
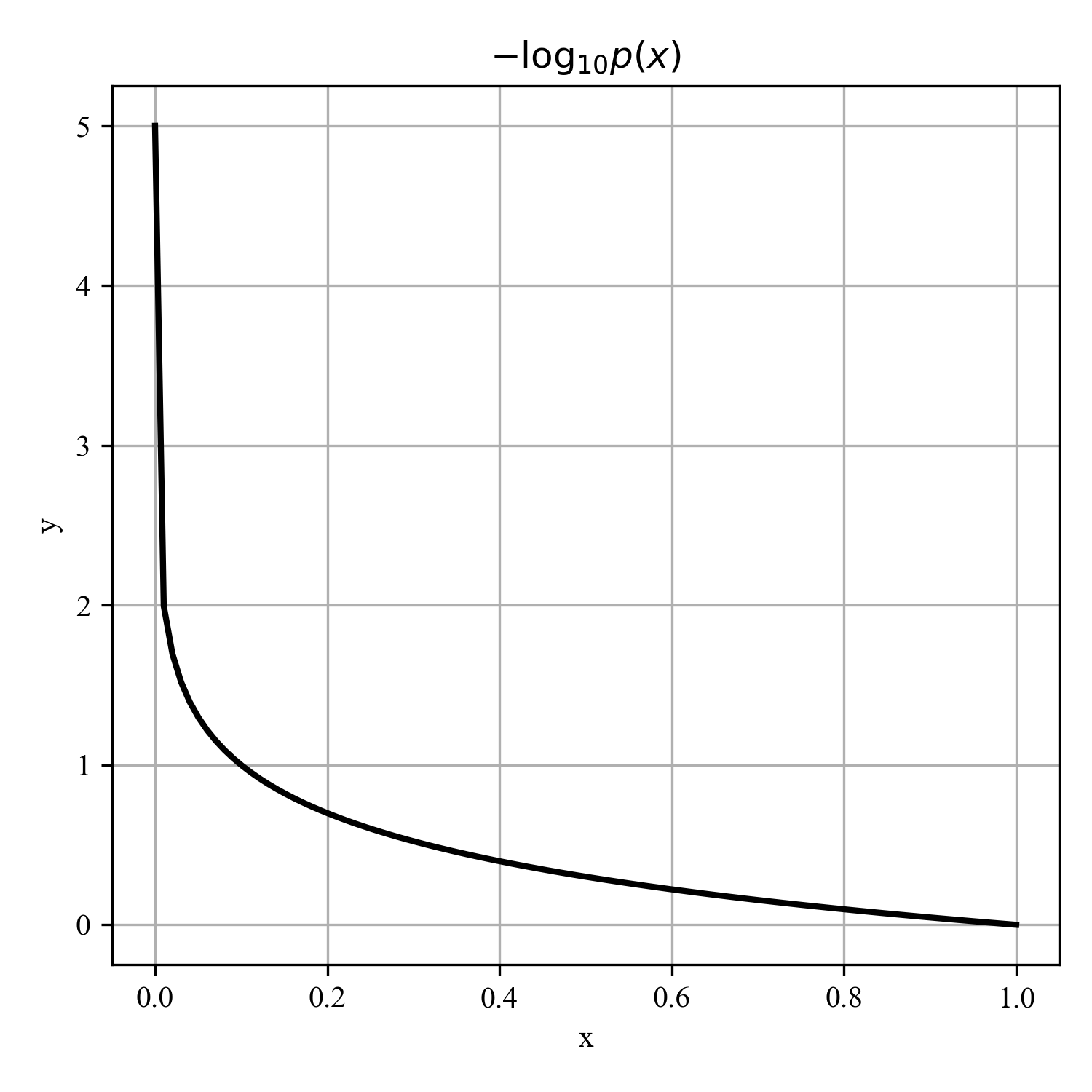
I(x)=−log(p(x))
我們再看看在定義域內,這個函數的走勢,如下圖:
熵
在自然生活中,我們所描述的事件並不是只有兩種狀態,例如擲骰子,結果會有6種可能,那麼如何衡量擲一次骰子的期望資訊量呢?這個所有期望的資訊量就是熵。
現在將一般問題抽象化,也就是對於某事件,事件狀態有 n n n種可能,每一種可能性都有一定概率 p ( x i ) p(x_i) p(xi)。那麼就可以根據這些概率資料計算各可能性的資訊量了,例如:
| 序號 | 事件 | 概率p | 資訊量I |
|---|---|---|---|
| A | 電腦正常開機 | 0.7 | -log(p(A))=0.36 |
| B | 電腦無法開機 | 0.2 | -log(p(B))=1.61 |
| C | 電腦爆炸了 | 0.1 | -log(p©)=2.30 |
注:上面的計算使用的是自然對數
熵的公式如下:
H
(
X
)
=
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
)
H(X) = - \sum_{i=1}^{n}p(x_i)log(p(x_i))
H(X)=−i=1∑np(xi)log(p(xi))
那麼這個"開電腦"的熵就是:
H
(
X
)
=
0.7
×
0.36
+
0.2
×
1.61
+
0.1
×
2.3
=
0.804
H(X) = 0.7\times 0.36 + 0.2\times 1.61 + 0.1 \times 2.3=0.804
H(X)=0.7×0.36+0.2×1.61+0.1×2.3=0.804
注:可能是一件事,但是不同描述就會有不同的熵,例如:開電腦我們通常就是兩種情況,就是能開機和不能開機,當你描述開電腦有第三種情況時,那麼這個事件就變了。
生活中還有一類比較特殊的問題如拋硬幣,結果只有兩種可能,正面和反面。正面、反面的結果在數學上就滿足0-1(二項)分佈。對於這種0-1分佈的問題,熵的計算就可以簡化,有如下公式:
H
(
X
)
=
−
p
(
x
)
log
p
(
x
)
−
(
1
−
p
(
x
)
)
log
(
1
−
p
(
x
)
)
H(X) = -p(x)\log p(x) - (1- p(x))\log (1- p(x))
H(X)=−p(x)logp(x)−(1−p(x))log(1−p(x))
相對熵(KL散度)
相對熵又稱KL散度,如果我們對於同一個隨機變數 x 有兩個單獨的概率分佈 P(x) 和 Q(x),我們可以使用 KL 散度(Kullback-Leibler (KL) divergence)來衡量這兩個分佈的差異。
在機器學習中,P往往用來表示樣本的真實分佈,比如[1,0,0]表示當前樣本屬於第一類。Q用來表示模型所預測的分佈,比如[0.7,0.2,0.1]
直觀的理解就是如果用P來描述樣本,那麼就非常完美。而用Q來描述樣本,雖然可以大致描述,但是不是那麼的完美,資訊量不足,需要額外的一些「資訊增量」才能達到和P一樣完美的描述。如果我們的Q通過反覆訓練,也能完美的描述樣本,那麼就不再需要額外的「資訊增量」,Q等價於P。
KL散度的計算公式:
D
K
L
(
p
∣
∣
q
)
=
∑
i
=
1
n
p
(
x
i
)
log
(
p
(
x
i
)
q
(
x
i
)
)
D_{KL}(p||q) = \sum_{i=1}^np(x_i)\log \left(\frac{p(x_i)}{q(x_i)}\right)
DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))
n為事件的所有可能性。
D
K
L
D_{KL}
DKL的值越小,表示q分佈和p分佈越接近。
交叉熵
將KL散度進行化簡有
D
K
L
(
p
∣
∣
q
)
=
∑
i
=
1
n
p
(
x
i
)
log
(
p
(
x
i
)
q
(
x
i
)
)
=
∑
i
=
1
n
p
(
x
i
)
log
(
p
(
x
i
)
)
−
∑
i
=
1
n
p
(
x
i
)
log
(
q
(
x
i
)
)
=
−
H
(
p
(
x
)
)
+
[
−
∑
i
=
1
n
p
(
x
i
)
log
(
q
(
x
i
)
)
]
\begin{aligned} D_{KL}(p||q) &= \sum_{i=1}^np(x_i)\log \left(\frac{p(x_i)}{q(x_i)}\right)\\ &= \sum_{i=1}^n p(x_i)\log\left( p(x_i) \right) - \sum_{i=1}^n p(x_i)\log \left(q(x_i) \right)\\ &= -H(p(x)) + [- \sum_{i=1}^np(x_i)\log(q(x_i))] \end{aligned}
DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))=i=1∑np(xi)log(p(xi))−i=1∑np(xi)log(q(xi))=−H(p(x))+[−i=1∑np(xi)log(q(xi))]
等式的第一部分就是p的熵,第二部分就是交叉熵,也稱為資訊增益:
H
(
p
,
q
)
=
−
∑
i
=
1
n
p
(
x
i
)
log
(
q
(
x
i
)
)
H(p, q)=-\sum_{i=1}^n p(x_i)\log(q(x_i))
H(p,q)=−i=1∑np(xi)log(q(xi))
在機器學習中,我們需要評估label和predict之間的差距,使用KL散度剛剛好,即:
D
K
L
(
y
∣
∣
y
^
)
D_{KL}(y||\hat{y})
DKL(y∣∣y^),由於KL散度中的前一部分
−
H
(
y
)
-H(y)
−H(y)不變,在優化的過程中只需要關注交叉熵就行了。所以一般在機器學習中可以直接使用交叉熵做損失函數,評估模型。
交叉熵損失函數
為什麼要用交叉熵做loss函數?
線上性迴歸中,常常使用MSE(Mean Squared Error)作為loss函數,如下:
l
o
s
s
=
1
2
m
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
loss = \frac{1}{2m}\sum_{i=1}^m(y_i -\hat{y_i})^2
loss=2m1i=1∑m(yi−yi^)2
其中
m
m
m表示樣本量。
在單標籤分類任務中,通常使用的就是交叉熵損失函數。所謂單標籤分類就是一個樣本就屬於一個類別。損失函數定義如下:
l
o
s
s
=
∑
i
=
1
n
y
i
log
(
y
i
^
)
loss = \sum_{i=1}^ny_i \log (\hat{y_i})
loss=i=1∑nyilog(yi^)
假如有如下預測結果:
| * | 貓 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 0 |
| Pred | 0.3 | 0.6 | 0.1 |
那麼該條樣本計算的損失值如下:
l
o
s
s
=
−
(
0
×
log
(
0.3
)
+
1
×
log
(
0.6
)
+
0
×
log
(
0.1
)
)
=
−
log
(
0.6
)
loss = - (0 \times \log(0.3) + 1\times \log(0.6) + 0\times \log(0.1)) = - \log (0.6)
loss=−(0×log(0.3)+1×log(0.6)+0×log(0.1))=−log(0.6)
對應一個batch資料loss值就是:
l
o
s
s
=
−
1
m
∑
j
=
1
m
∑
i
=
1
n
y
j
i
log
(
y
j
i
^
)
loss = - \frac{1}{m}\sum_{j=1}^{m}\sum_{i=1}^{n} y_{ji} \log\left(\hat{y_{ji}}\right)
loss=−m1j=1∑mi=1∑nyjilog(yji^)
其中m為batch的批次數量。
當然實際任務中不僅有單標籤的資料,還有多標籤資料。假如有如下預測結果資料:
| * | 貓 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 1 |
| Pred | 0.1 | 0.7 | 0.8 |
注:這裡你會發現pred的和不是1,這裡對每個預測結果進行了sigmoid處理,而不是使用softmax,那麼每個類別的打分輸出結果就被歸一化到(0,1)之間了。這裡也就認為各個標籤都是獨立分佈的,相互之間沒有影響。這時,交叉熵在這裡是單獨對每一個類別進行計算,每個類別就只有兩種可能,算作一種二項分佈了。那麼對於一條樣本就可以得到以下結果:
l
o
s
s
c
a
t
=
−
0
×
log
(
0.1
)
−
(
1
−
0
)
×
log
(
1
−
0.1
)
=
−
log
(
0.9
)
l
o
s
s
f
r
o
g
=
−
1
×
log
(
0.7
)
−
(
1
−
1
)
×
log
(
1
−
0.7
)
=
−
log
(
0.7
)
l
o
s
s
m
o
u
s
e
=
−
1
×
log
(
0.8
)
−
(
1
−
1
)
×
log
(
1
−
0.8
)
=
−
log
(
0.8
)
l
o
s
s
=
l
o
s
s
c
a
t
+
l
o
s
s
f
r
o
g
+
l
o
s
s
m
o
u
s
e
\begin{array}{c} loss_{cat} = -0\times \log(0.1) - (1-0)\times\log(1-0.1) = - \log(0.9)\\ loss_{frog} = -1\times \log(0.7) - (1-1)\times \log(1-0.7) = - \log(0.7)\\ loss_{mouse} = -1\times \log(0.8) - (1-1)\times \log(1-0.8) = - \log(0.8)\\ loss = loss_{cat} + loss_{frog} + loss_{mouse} \end{array}
losscat=−0×log(0.1)−(1−0)×log(1−0.1)=−log(0.9)lossfrog=−1×log(0.7)−(1−1)×log(1−0.7)=−log(0.7)lossmouse=−1×log(0.8)−(1−1)×log(1−0.8)=−log(0.8)loss=losscat+lossfrog+lossmouse
同理對於一個batch資料的loss則有:
loss
=
1
m
∑
j
=
1
m
∑
i
=
1
n
−
y
j
i
log
(
y
j
i
^
)
−
(
1
−
y
j
i
)
log
(
1
−
y
j
i
^
)
\operatorname{loss}=\frac{1}{m}\sum_{j=1}^{m} \sum_{i=1}^{n}-y_{j i} \log \left(\hat{y_{j i}}\right)-\left(1-y_{j i}\right) \log \left(1-\hat{y_{j i}}\right)
loss=m1j=1∑mi=1∑n−yjilog(yji^)−(1−yji)log(1−yji^)
其中m為一個batch中樣本數目。