概率論必背知識點
理解背誦
概率基礎
條件概率,乘法公式
全概率公式
貝葉斯公式
一維隨機變數
離散型隨機變數 分佈律,分佈函數
連續性隨機變數 分佈函數,概率密度
連續性隨機變數函數 概率密度:單調、普通(分佈函數--求導-->概率密度)
二項分佈 X~B(n,p) 分佈律 E(X)=np D(X)=np(1-p)
泊松分佈X~P(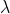 ) 分佈律P{X=k}=
) 分佈律P{X=k}=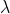 ^k/k! e^(-
^k/k! e^(-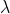 ) E(X)=D(X)=
) E(X)=D(X)=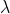
均勻分佈X~U(a,b) 概率密度 E(x)=1/2(a+b) D(X)=(b-a)^2/12
指數分佈X~E(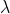 ) 概率密度=
) 概率密度=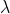 e^(-
e^(-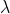 x) E(x)=1/
x) E(x)=1/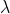 D(X)=1/
D(X)=1/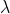 ^2
^2
正態分佈X~N(u ,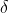 ^2) 概率密度 E(X)=u D(X)=
^2) 概率密度 E(X)=u D(X)=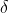 ^2
^2
標準正態分佈 標準化變化
卡方分佈X^2(n) E(X)=n D(X)=2n
二維隨機變數
離散型二維隨機變數 聯合分佈律 判斷x,y是否獨立:分佈律判斷
連續型二維隨機變數 聯合概率密度 邊緣概率密度 條件概率密度 判斷x,y是否獨立:邊緣概率密度 判斷
連續型二維隨機變數函數 Z=X+Y Z=XY Z=max{X,Y}
數學期望,方差,協和差
離散型隨機變數 數學期望
離散型隨機變數函數 數學期望
連續性隨機變數 數學期望
![]()
連續性隨機變數函數 數學期望
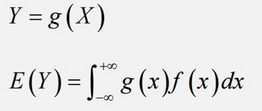
方差 基本定義式 公式
期望的運算規則
方差的運算規則
離散型二維隨機變數 數學期望E(XY)=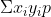
連續型二維隨機變數 數學期望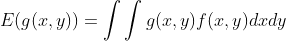
協和差 Cov(X,Y)=Cov(Y,X) Cov(aX+b,Y)=aCov(X,Y) Cov(X1+X2,Y)=Cov(X1,y)+Cov(X2,Y)
相關係數 獨立一定不相關,不相關不一定獨立
切比雪夫不等式
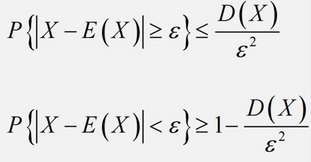
大數定理及中心極限定理
獨立、同分布中心極限定理 獨立、同分布、期望、方差存在、求和 p公式
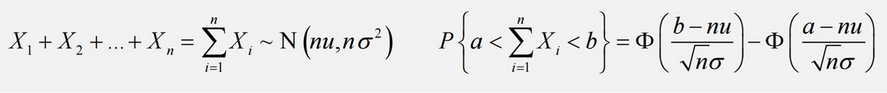
二項分佈中心極限定理 X~B(n,p)近似與N(np,np(1-p)) p公式
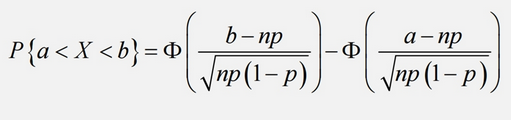
抽樣分佈
常用統計量 樣本均值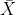 樣本方差
樣本方差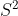 =總體方差
=總體方差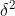 /n
/n
常考性質 樣本均值的期望為總體期望 樣本方差=總體方差/n 樣本方差期望=總體方差
樣本均值與樣本方差相互獨立
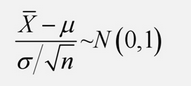 樣本均值和樣本方差標準化近似於標準正態分佈
樣本均值和樣本方差標準化近似於標準正態分佈
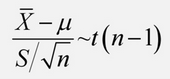
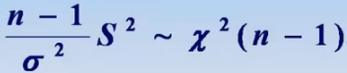
三種常見分佈
卡方分佈 n個 獨立 標準正太分佈 的平方和 服從自由度為n的卡方分佈
性質 兩個卡方分佈的和 服從 自由度為自由度和 的卡方分佈
上側分位數 卡方分佈大於一個常數的概率為卡方分佈的下標
t分佈 獨立 標準正太分佈 除以 根號下自由度為n的卡方分佈除以n 的分佈服從自由度為n的t分佈
性質 ![]()
F分佈 獨立 自由度為n1的卡方分佈 除以 n1 除以 自由度為n2的卡方分佈 除以 n2 的分佈服從自由度為(n1,n2)的F分佈
性質 自由度順序相反的F分佈互為倒數

自由度順序相反的F分佈互為倒數,且F下標和為1
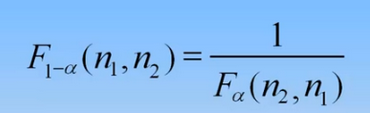
引數估計
矩估計 u1=E(X)=f( ) 反解引數
) 反解引數
 的矩估計量為反解函數用
的矩估計量為反解函數用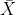 替換u1
替換u1
最大似然估計 構造似然函數為概率密度函數連乘 取對數 對引數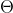 求導 解出最大似然估計量
求導 解出最大似然估計量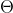 (X變為大寫)
(X變為大寫)
無偏估計 E( )=
)=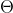 則
則 是
是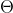 的無偏估計
的無偏估計
估計量的優良性準則 無偏性 有效性 相合性
區間估計
置信區間求解 ①定型別,擺公式 ②計算各分量 ③代入公式

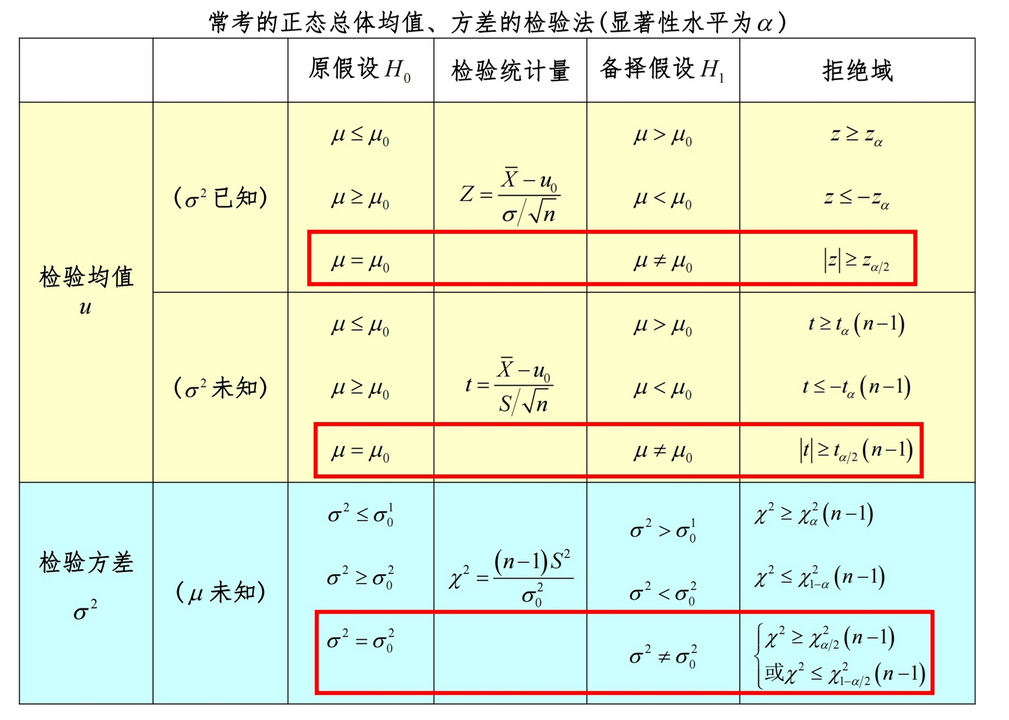
假設檢驗
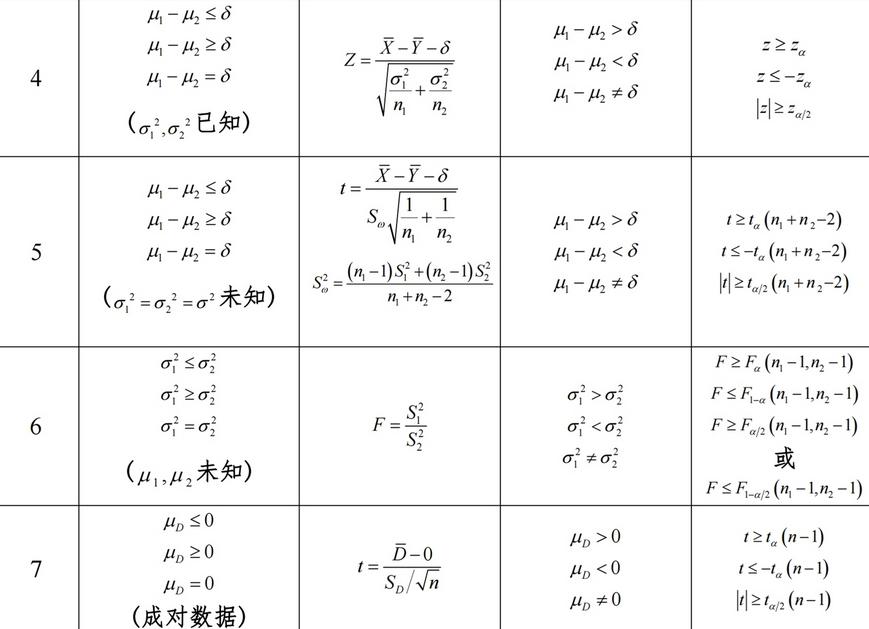
假設檢驗 提出假設:H0和H1 定型別,擺公式 計算統計量和拒絕域 定論、總結
兩類錯誤 一棄真,二取偽
迴歸分析
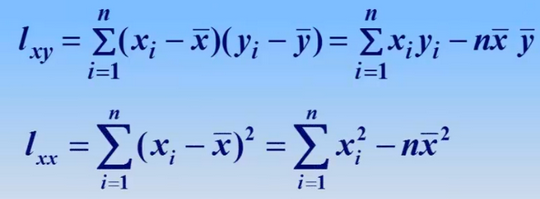

相關係數