2.C++-選擇排序、氣泡排序、插入排序、希爾排序、歸併排序、快速排序
1.常用排序演演算法介紹
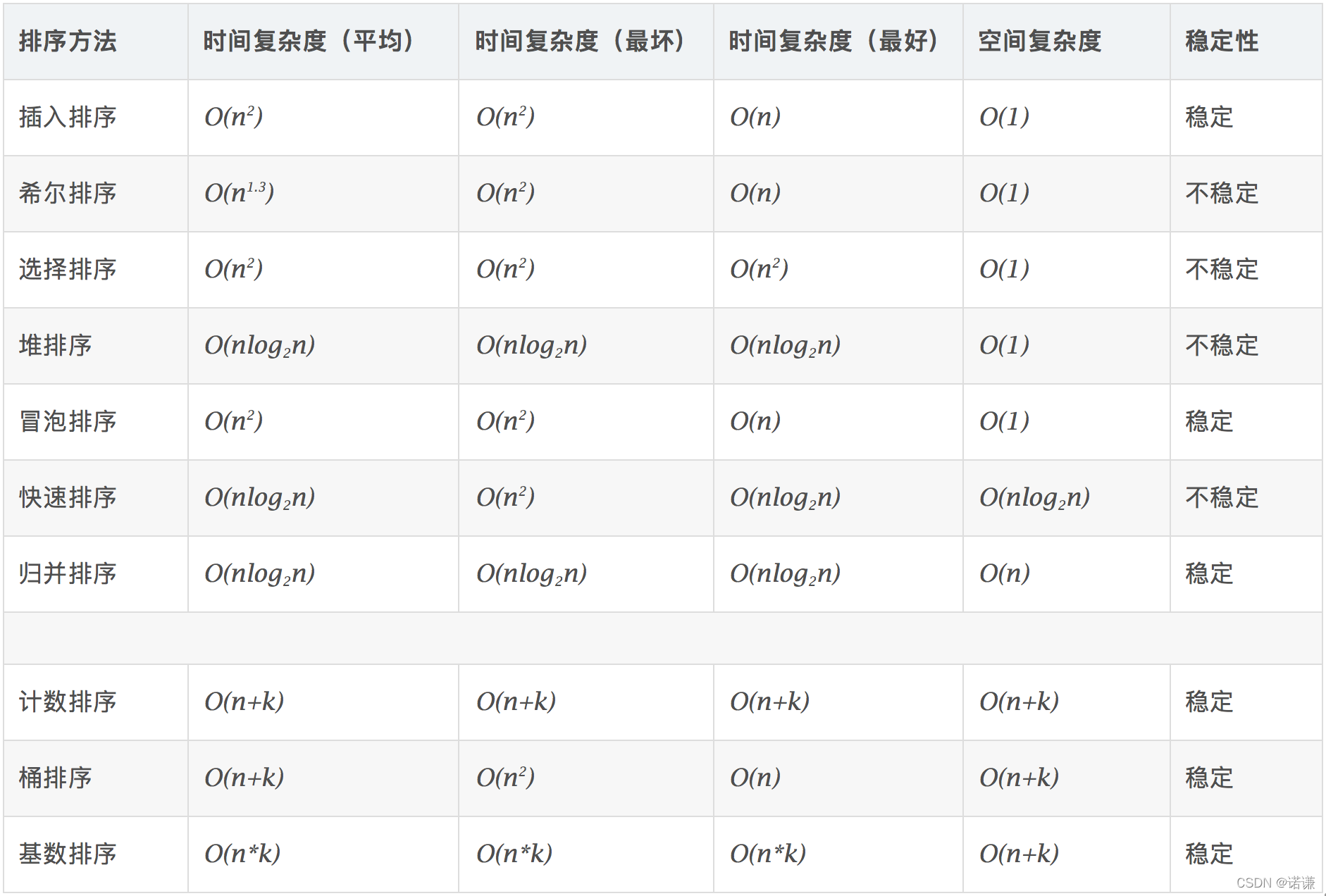
一個排序演演算法的好壞需要針對它在某個場景下的時間複雜度和空間複雜度來進行判斷、並且排序都需要求其穩定性,比如排序之前a在b前面,且a=b,排序之後也要保持a在b前面、
常用排序演演算法如下所示:
2.選擇排序
首先i等於0,每次i++,並從i輪詢到末尾,選擇一個最小者與第i個位置進行交換.
比如:
16,8,21,10,49
第1次遍歷整個陣列,找到最小值8,則與arr[0]進行交換:
8,16,21,10,49
第2次遍歷下標1~4的陣列,找到10,則與arr[1]進行交換:
8,10 ,21,16,49
第3次遍歷下標2~4的陣列,找到16,則與arr[2]進行交換:
8,10 , 16, 21,49
第4次遍歷下標3~4的陣列,找到21,由於交換的位置相等,則保持不變
由於第5次,起始小標等於n-1了.所以已經比較完了.則結束了.
所以程式碼如下所示:
template <typename T>
void mySwap(T& a, T& b) // 交換函數
{
T c(a);
a = b;
b = c;
}
template <typename T>
void seleteSort(T arr[], int len, bool ascend = true) // ascend為ture表示升序
{
for (int i = 0; i < len -1; ++i) {
int minIdx = i;
for (int j = i+1; j < len; ++j) {
if (ascend ? (arr[minIdx] > arr[j]) : (arr[minIdx] < arr[j])) {
minIdx = j;
}
}
if (minIdx != i) {
mySwap(arr[i], arr[minIdx]);
}
}
}測試程式碼如下所示:
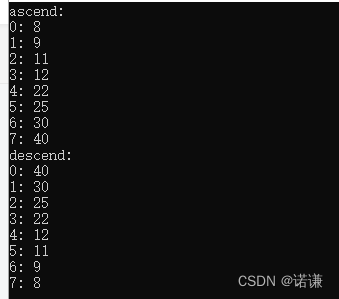
int arr[8] = {25, 22, 12, 8, 9, 11, 30 ,40};
bubbleSort(arr, 8);
cout<<"ascend: "<<endl;
for (int i = 0; i < 8; ++i) {
cout<<i<<": "<<arr[i]<<endl;
}
bubbleSort(arr, 8, false);
cout<<"descend: "<<endl;
for (int i = 0; i < 8; ++i) {
cout<<i<<": "<<arr[i]<<endl;
}列印如下所示:
總結:
選擇排序是不穩定的排序演演算法,例如 [3, 4, 3, 1, 5]這個陣列,第一次交換,第一個3和1交換位置,此時原來兩個3的相對位置發生了變化,所以無法保證值相等的元素的相對位置不變,
3.氣泡排序
重複len次冒泡,每次冒泡都是(int j=len-1; j>i; j--)從陣列末尾往前進行冒泡,如果arr[j-1]>arr[j],則將arr[j]與arr[j-1]交換,讓值小的冒泡上去.
程式碼如下所示:
template < typename T >
static void bubbleSort(T arr[], int len, bool ascend = true)
{
bool isSwap = true;
for(int i=0; (i<len) && isSwap; i++) // 每次冒泡時,則判斷上次是否發生過交換,如果交換過,那說明還不是個有序的表
{
isSwap = false; // 每次冒泡的時候復位 「交換標誌位」
for(int j=len-1; j>i; j--)
{
if( ascend ? ( arr[j-1] > arr[j] ) : (arr[j-1] < arr[j] ) ) // 如果是升序,arr[j-1] > arr[j],則將arr[j]從末尾冒泡冒上去
{
mySwap(arr[j], arr[j-1]);
isSwap = true; // 「交換標誌位」 設定為true
}
}
}
}PS: 由於mySwap()函數和測試程式碼已經寫過了,後面就不再重複寫了。
總結:
氣泡排序是穩定的排序演演算法,因為每次都是冒泡相鄰比較,比如升序,如果後者>=前者,是不會進行交換
4.插入排序
將一個陣列分為兩個部分,左邊是排序好的,右邊是未排序的.
然後每次提取一個右邊的資料出來,然後輪詢左邊(排序好的),如果找到合適的位置(前者小於它且後者大於它),則插入進去.如果未找到,則插入在左邊排序好的末尾位置.
比如16,8,21,10,49,由於左邊預設會有一個數值(一個數值無需判斷比較),所以無需判斷arr[0]:
16 | 8,21,10,49 ( |左邊是排序好的,右邊是等待排序的 )
第1次,獲取arr[1],由於8小於16,插入在16前面,所以插入後:
8,16 | 21,10,49
第2次,獲取arr[2],向前輪詢,由於21>16,所以停止向前遍歷, 並且位置沒改變過,所以無需操作:
8,16,21 | 10,49
第3次,獲取arr[3], 向前輪詢,由於10<21,則21向後挪位,再繼續向前輪詢,由於10<16,則16向後挪位,最後10>=8,則插入在8後面:
8, 10,16,21 | 49
第4次,獲取arr[4],由於49>21,所以停止向前遍歷, 並且位置沒改變過,所以無需操作最終為:
8, 10,16,21 ,49
程式碼如下所示:
template < typename T >
static void insertSort(T arr[], int len, bool ascend = true)
{
for(int i=1; i<len; i++) // 迴圈取出右邊未排序的
{
int k = i;
T temp = arr[i]; // 把值取出來,後面會進行挪位元運算,會覆蓋掉arr[i]原來的內容
// 如果ascend為true,則表示升序,那麼當後者大於前者時,則停止for輪詢,因為左邊是有序序列
for(int j=i-1; (j>=0) && (ascend ? (arr[j]>temp) : (arr[j]<temp)); j--)
{
arr[j+1] = arr[j]; // 進行先後挪位元運算
k = j; // 更新要插入的位置
}
if( k != i ) // 如果未進行挪位,那麼k==i,則不需要重複插入
{
arr[k] = temp;
}
}
}
總結:
插入排序是穩定的排序演演算法,例如 [4,3, 3, 1, 5]這個陣列,由於左邊的3是提前插入的[ 3, 4 | 3, 1, 5],而後續的3由於>=前面的3,所以插入在後面
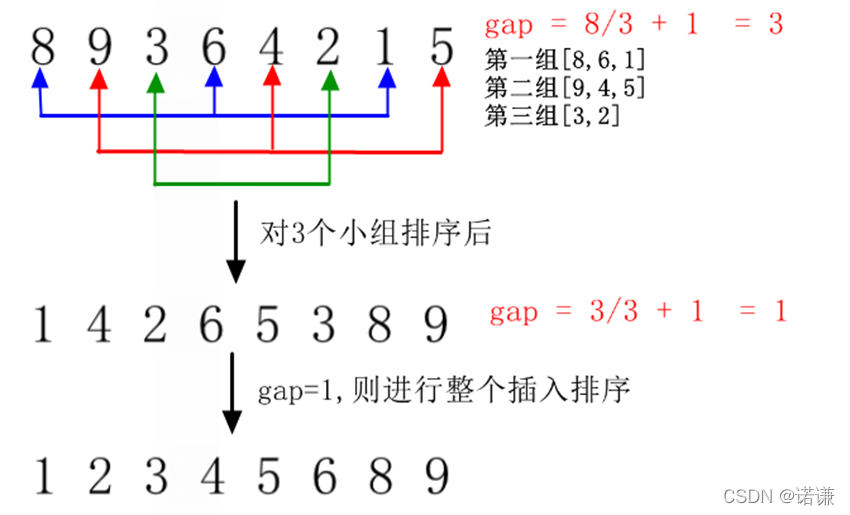
5.希爾排序
希爾排序是插入排序的升級版.並且比插入排序快.
希爾排序則是將一個插入排序,比如初始步長間隔gap為3,那麼將會分成3個小組進行插入排序,每個小組插入排序好後,再次將步長間隔gap較少一部分再次進行插入排序,直到最後步長偏移為1後,進行整個插入排序.一般gap步長都是以 len/3+1來計算.以後每次以 gap/3+1來縮小。
PS: 也可以設定gap固定增量從 n/2 開始,以後每次縮小到原來的一半。
比如下圖所示:
程式碼如下所示:
template < typename T >
static void shellSort(T arr[], int len, bool ascend = true)
{
int gap = len;
while (gap > 1) {
gap = gap / 3 + 1; // 加一能夠保證gap最後一次為1.
for(int offset = 0 ; offset < gap; ++offset) { // 對每組進行插入排序
for(int i=gap-offset; i<len; i+=gap) // 迴圈取出右邊未排序的
{
int k = i;
T temp = arr[i]; // 把值取出來,後面會進行挪位元運算,會覆蓋掉arr[i]原來的內容
// 假如ascend為true,則表示升序,那麼當後者大於前者時,則停止for輪詢
for(int j=i-gap; (j>=0) && (ascend ? (arr[j]>temp) : (arr[j]<temp)); j-=gap)
{
arr[j+gap] = arr[j]; // 進行先後挪位元運算
k = j; // 更新要插入的位置
}
if( k != i ) // 如果未進行挪位,那麼k==i,則不需要重複插入
{
arr[k] = temp;
}
}
}
}
}
總結:
希爾排序是不穩定的排序演演算法,因為希爾排序通過分組方法,可能會將最後的值跳過中間重複的值排序到前面
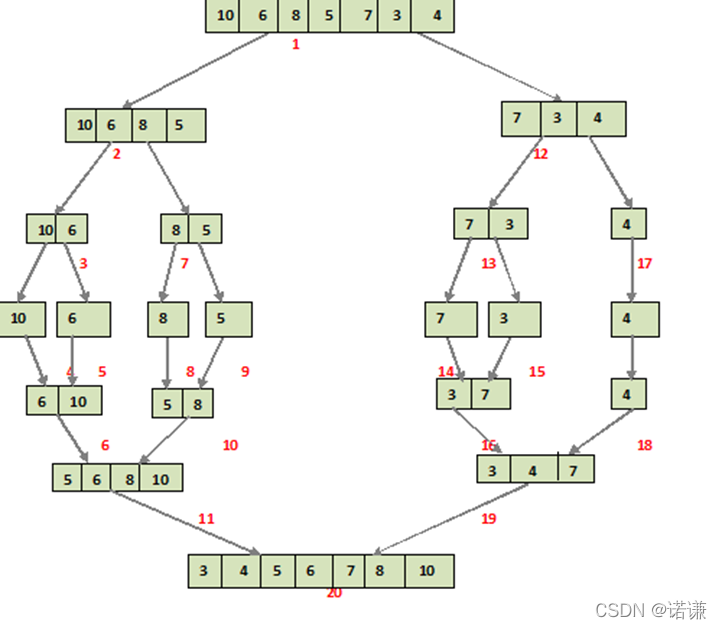
6.歸併排序
歸併是將兩個或多個有序序列合併成一個新的有序序列。歸併方法有多種,一次對兩個有序記錄序列進行歸併,稱為二路歸併排序,也有三路歸併排序及多路歸併排序。本程式碼是二路歸併排序.
思路如下所示:
通過遞迴的方式將一個無序序列,對半拆解、直到不能拆解時,則進行兩路比較排序(歸併)到一個輔助空間陣列中,歸併完成後則將輔助陣列中內容拷貝回去,返回上一級遞迴再進行兩路比較排序(歸併)和拷貝.直到最後則整個序列歸併完成.
如下圖所示(紅色數位表示遞迴拆解和歸併的先後順序):
程式碼如下所示:
template < typename T >
static void merge(T arr[], int l, int mid, int r, bool ascend = true) // 進行比較歸併
{
int n = r - l + 1;
T* helper = new T[n]; // 建立一個輔助空間,用來臨時儲存
int i = 0;
int left = l;
int right = mid+1;
while (left <= mid && right <= r) {
// 如果ascend = true, 則判斷左邊如果大於右邊的,則存放右邊的
if (ascend ? arr[left] > arr[right] : arr[left] < arr[right])
helper[i++] = arr[right++];
else
helper[i++] = arr[left++];
}
// 將某一側剩餘的存放進去
while (left <= mid)
helper[i++] = arr[left++];
while (right <= r)
helper[i++] = arr[right++];
// 最後將排序好的替換到原陣列
for (i = 0; i < n; ++i) {
arr[l + i] = helper[i];
}
delete [] helper;
}
template < typename T >
static void mergeSort(T arr[], int l, int r, bool ascend = true) // 遞迴拆解
{
if (l >= r) // 不能再進行拆解了,直接退出
return;
int mid = (l+r)/2;
mergeSort(arr, l, mid, ascend);
mergeSort(arr, mid+1, r, ascend);
merge(arr, l, mid, r, ascend);
}
template < typename T >
static void mergeSort(T arr[], int len, bool ascend = true)
{
mergeSort(arr, 0, len-1, ascend);
}總結:
由於歸併排序需要使用一個輔助空間,所以空間複雜度為O(n),由於都是附近的兩兩比較,所以是個穩定的演演算法.
7.快速排序
快速排序是氣泡排序的一種改進,主要的演演算法思想是在待排序的 n 個資料中取第一個資料作為Pivot基準值,然後採用二分的思想,把大於Pivot的資料放在右邊,把小於Pivot的資料放在左邊。最後確定Pivot基準值的中間位置.然後再次遞迴進行左右分割區確定基準值,直到左右兩邊都是一個數值時,則完成排序.
如下圖所示:
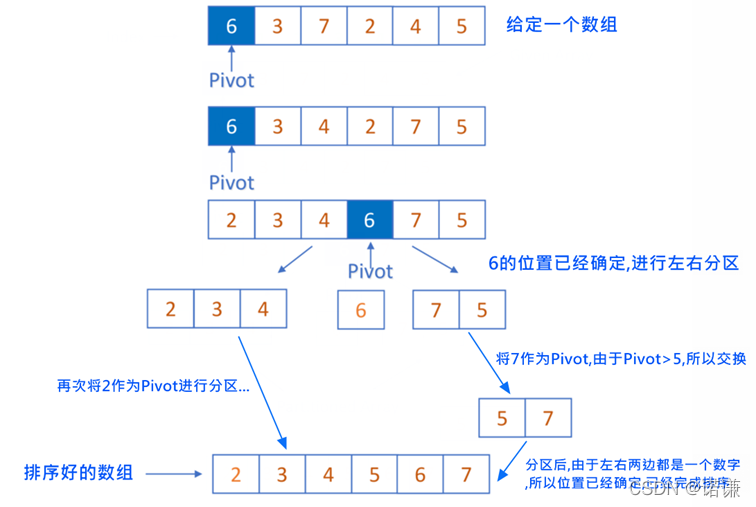
步驟如下:
1) 設定兩個變數l、r,排序開始的時候:l=0,r=n-1;
2)第一個陣列值作為Pivot基準值,pivot=arr[0];
3)然後r-- ,向左搜尋,找到小於pivot後,因為arr[l]的值儲存在pivot中,所以直接賦值,s[l]=s[r]
4)然後l++,向右搜尋,找到大於pivot後,因為arr[r]的值儲存在第2步的s[l]中,所以直接賦值,s[r]=s[l],然後r--,避免死迴圈
5)重複第3、4步,直到l=r,最後將pivot值放在arr[l]中(確定了位置)
6) 然後採用「二分」的思想,以i為分界線,拆分成兩個陣列 s[0,l-1]、s[l+1,n-1]又開始排序
程式碼如下所示:
template < typename T >
static void quickSort(T arr[], int left, int right, bool ascend = true)
{
if (left>=right)
return;
int l =left, r = right;
T pivot = arr[l]; // 預設將最左邊的設定為基值
while(l<=r) {
while(r > l && (ascend ? arr[r] >= pivot : arr[r] <= pivot)) r--;
arr[l] = arr[r]; // 由於arr[l]已經存放在pivot了,所以直接替換
while(l < r && (ascend ? arr[l] <= pivot: arr[r] >= pivot)) l++;
arr[r--] = arr[l]; // 由於arr[r]之前的值已經存在了左邊,所以直接替換
}
arr[l]=pivot; // 最後找到基值的位置
quickSort(arr, left, l-1, ascend);
quickSort(arr, l+1, right, ascend);
}
template < typename T >
static void quickSort(T arr[], int len, bool ascend = true)
{
quickSort(arr, 0, len-1, ascend);
}
總結:
由於快速排序是判斷Pivot基準值的排序,可能會將後者的某個相等的數放在最前面, 是個不穩定的演演算法.
快速排序比歸併排序總結
由於歸併排序涉及記憶體讀寫、所以快速排序比歸併排序快、但是快速排序是個不穩定的演演算法、但是如果在區域性大部分有序的情況下,還是使用歸併排序快