多元線性迴歸模型的各種診斷

提示：
①這裡沒有原理，只有R的程式碼、執行結果以及對部分結果的解讀！！！
②有重複的部分，節約時間的話可以重點看標黃的地方.

例一強影響點診斷

資料說明在這裡插入圖片描述
迴歸分析：

在這裡插入圖片描述
從結果中可以看出，迴歸係數並不顯著，模型的擬合效果不好.

學生化殘差：
在這裡插入圖片描述
繪製殘差圖：

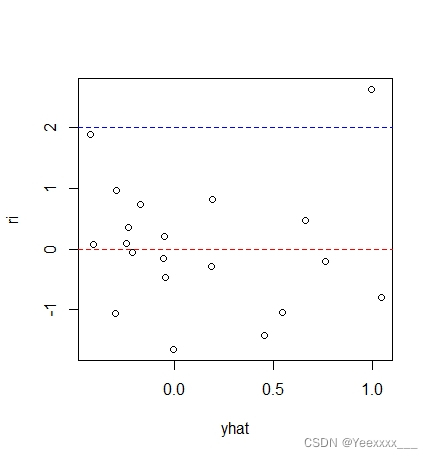
從殘差圖中可以看出，大部分資料位於兩倍標準差內. 殘差有遞減的趨勢，因而隨機誤差項的齊性假設可能不太合理.

繪製迴歸診斷圖:
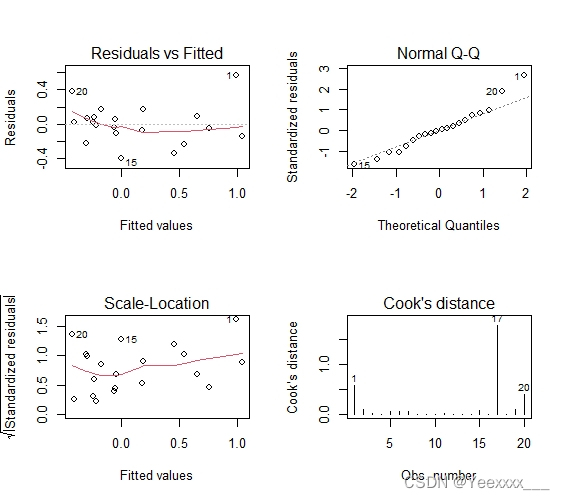
在這裡插入圖片描述
Residuals vs Fitted：殘差與估計值之間的關係，資料點應該大致落在兩倍標準差也就是2、-2之間，且這些點不應該呈現任何有規律的趨勢.
Normal QQ：若滿足正態假設，那麼圖上的點應該落在呈45度角的直線上；若不是如此，那麼就違反了正態性的假設.
Scale-Location：GM假設中的同方差可以通過這張圖診斷，方差應該呈現基本確定或持平的樣子.
Cook’s distance：Cook距離，用於強影響點的診斷.

影響分析：
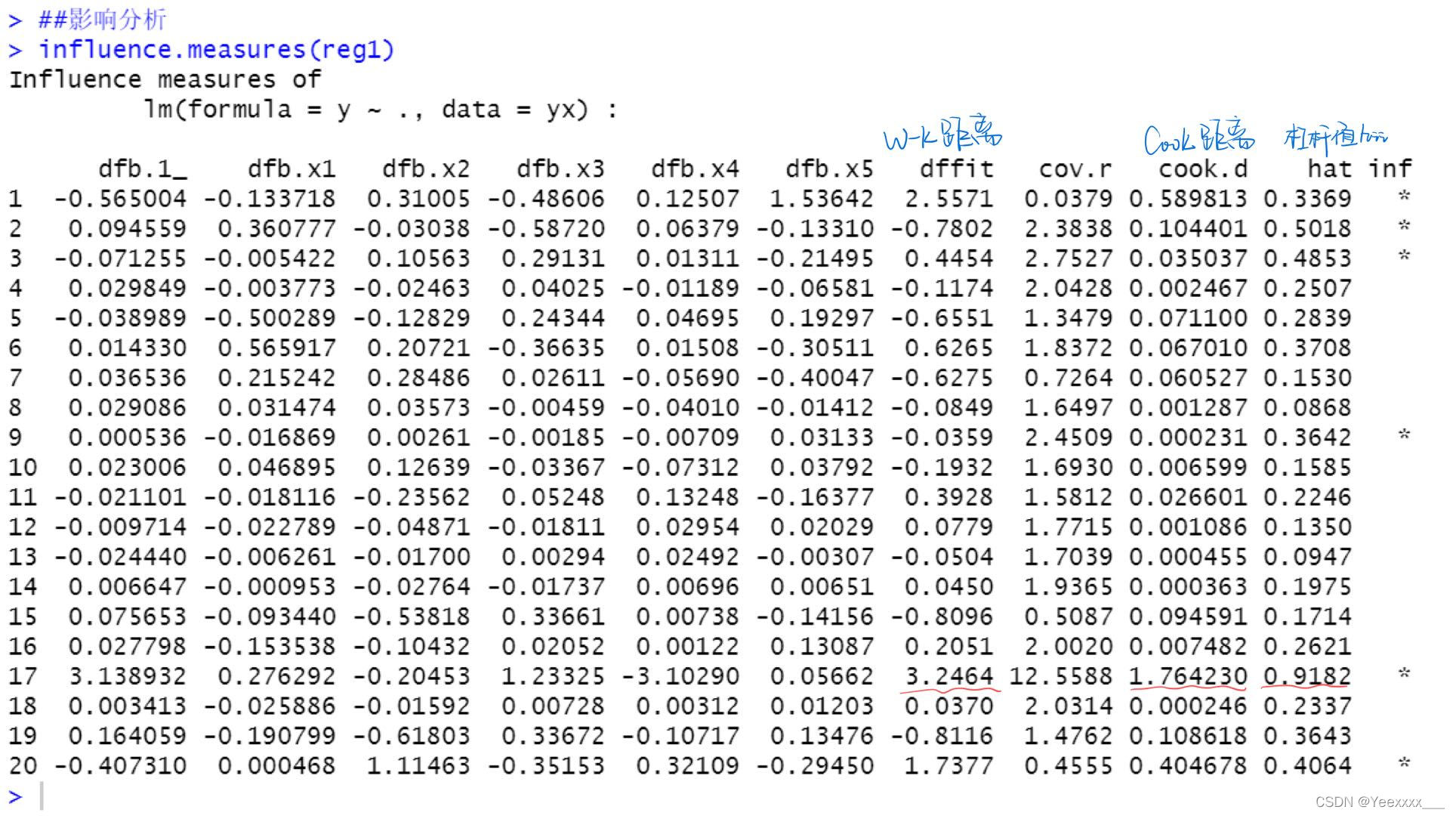
在這裡插入圖片描述
17號點的各種影響度量都很大，所以認為17號資料點是強影響點. 使用car包的influencePlot()函數，找出影響迴歸的異常點和強影響點.

在這裡插入圖片描述

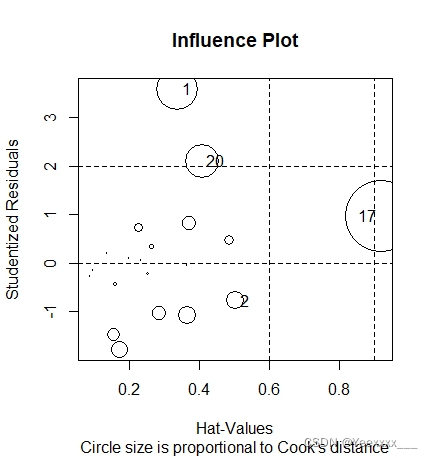
圖中圓很大的點可能是對模型引數的估計造成的較強影響的強影響點.

code:

yx=read.table("eg5.6_ch5.txt",header=T)
yx

reg1=lm(y~.,data=yx)
summary(reg1)

sse = 0.2618**2*14
r2 =0.8104
sst = sse/(1-r2)
Ft = 11.97
ssr = sst - sse;ssr
(ssr/5)/(sse/14)

##學生化殘差
rstandard(reg1)  # 學生化內殘差
0.562611/(0.2618*sqrt(1-0.3369))
rstudent(reg1)  # 學生化外殘差


##殘差圖
ri=rstandard(reg1)
yhat=predict(reg1);yhat  # y的估計
plot(ri~yhat)
abline(h=0,col="red",lty="dashed")
abline(h=2,col="blue",lty="dashed")

##殘差診斷圖4張
op<-par(mfrow=c(2,2))   # 2*2子圖
plot(reg1,1:4)
par(op)

##影響分析
influence.measures(reg1)

library(car)
influencePlot(reg1,main="Influence Plot",sub="Circle size is proportional to Cook's distance")

例二異方差性診斷

迴歸分析：
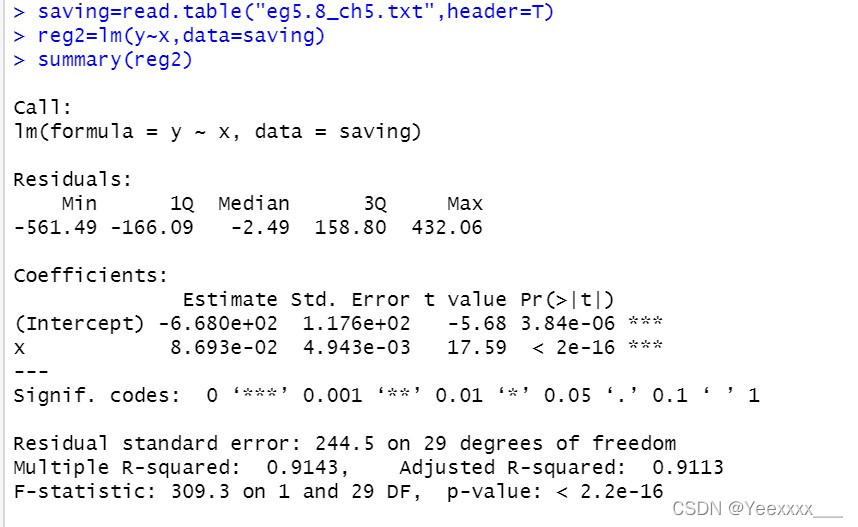
在這裡插入圖片描述
回憶一下怎麼讀這個結果

繪製殘差圖：
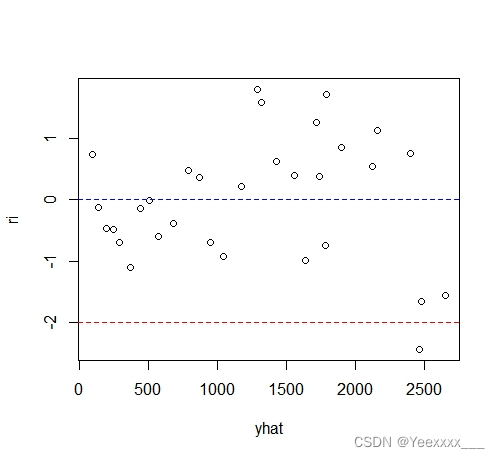
在這裡插入圖片描述

從圖中可以看出，從左到右各個點逐漸散開，說明誤差項具有異方差性.

等級相關係數法檢驗異方差性：
在這裡插入圖片描述
$H_0:r_s=0$ (同方差)， $H_1:r_s\neq0$ (異方差). 所以在0.05的顯著性水平下，p值 $0.001301 < 0.05$ ，拒絕原假設，說明隨機誤差項存在異方差性.

BP檢驗：
在這裡插入圖片描述

p值和顯著性水平 $\alpha$ 比較，和等級相關係數法一樣.

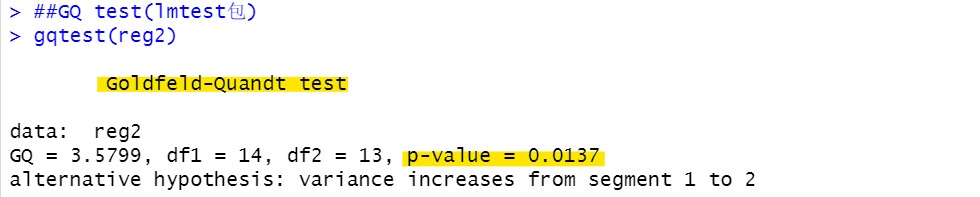
GQ檢驗:
在這裡插入圖片描述
White檢驗：

通過加權最小二乘修正異方差：
(anova方差分析)

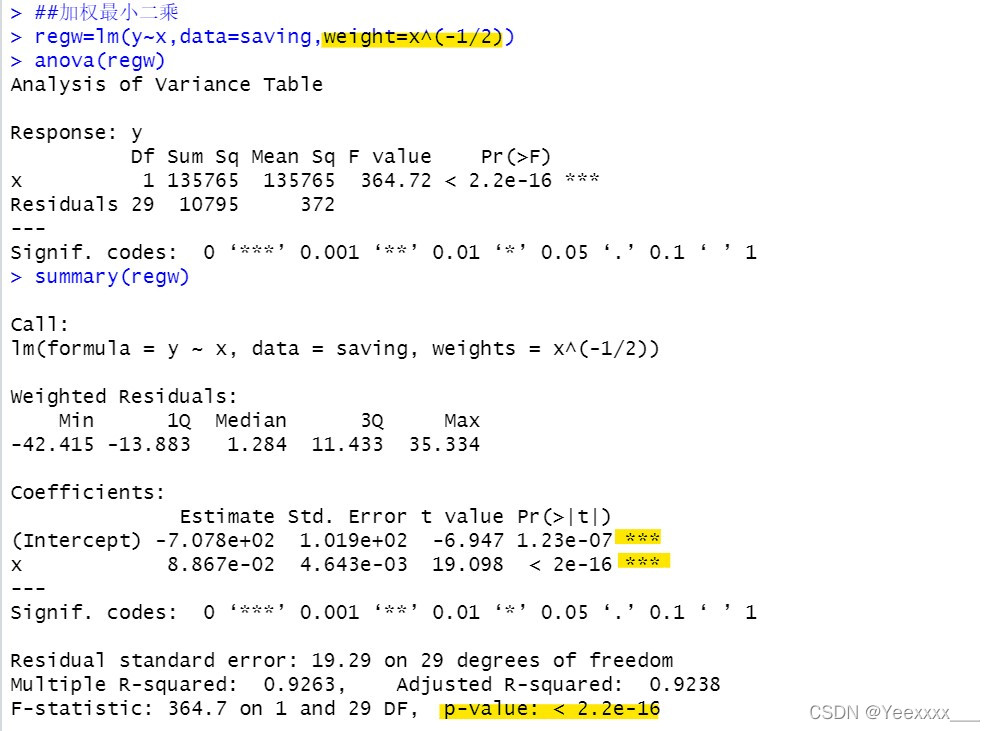
修正異方差性後模型的結果更加精確.

code：

saving=read.table("eg5.8_ch5.txt",header=T)

reg2=lm(y~x,data=saving)
summary(reg2)

plot(y~x,data=saving,col="red")
abline(reg2,col="blue")

##殘差圖
ri=rstandard(reg2)
yhat=predict(reg2)
plot(ri~yhat)
abline(h=0,col="blue",lty="dashed")
abline(h=-2,col="red",lty="dashed")

##spearman test
abe=abs(reg2$residual)
cor.test(~abe+x,data=saving,method="spearman")

##BP test
#檢驗結果
library(lmtest)
library(zoo)
bptest(reg2,studentize=FALSE)
bptest(reg2) #學生化具有修正異方差的作用

#輔助迴歸結果
e=residuals(reg2)
e2=(reg2$residuals)^2;
lmre=lm(e2~saving$x)
summary(lmre)
LM=31*0.2723; LM

##GQ test(lmtest包)
gqtest(reg2)

##white test(whitestrap包)
#檢驗結果
# install.packages('whitestrap')
library(whitestrap)
white_test(reg2)

#輔助迴歸結果
x=saving$x
lmre2=lm(e2~x+I(x^2))
summary(lmre2)
white=31*0.2974; white

##加權最小二乘
regw=lm(y~x,data=saving,weight=x^(-1/2))
anova(regw)
summary(regw)

例三自相關性診斷

(和例二是同一份資料)

DW檢驗: 記得看適用條件！！！
在這裡插入圖片描述
DW=1.2529，R不會直接給對應的上下限，所以需要自己查DW分佈表中的上下限，與DW比較. 或者看p值，p-value=0.008674與顯著性水平 $\alpha$ 比較，若 $p<\alpha$ 拒絕原假設，認為存在一階自相關性.
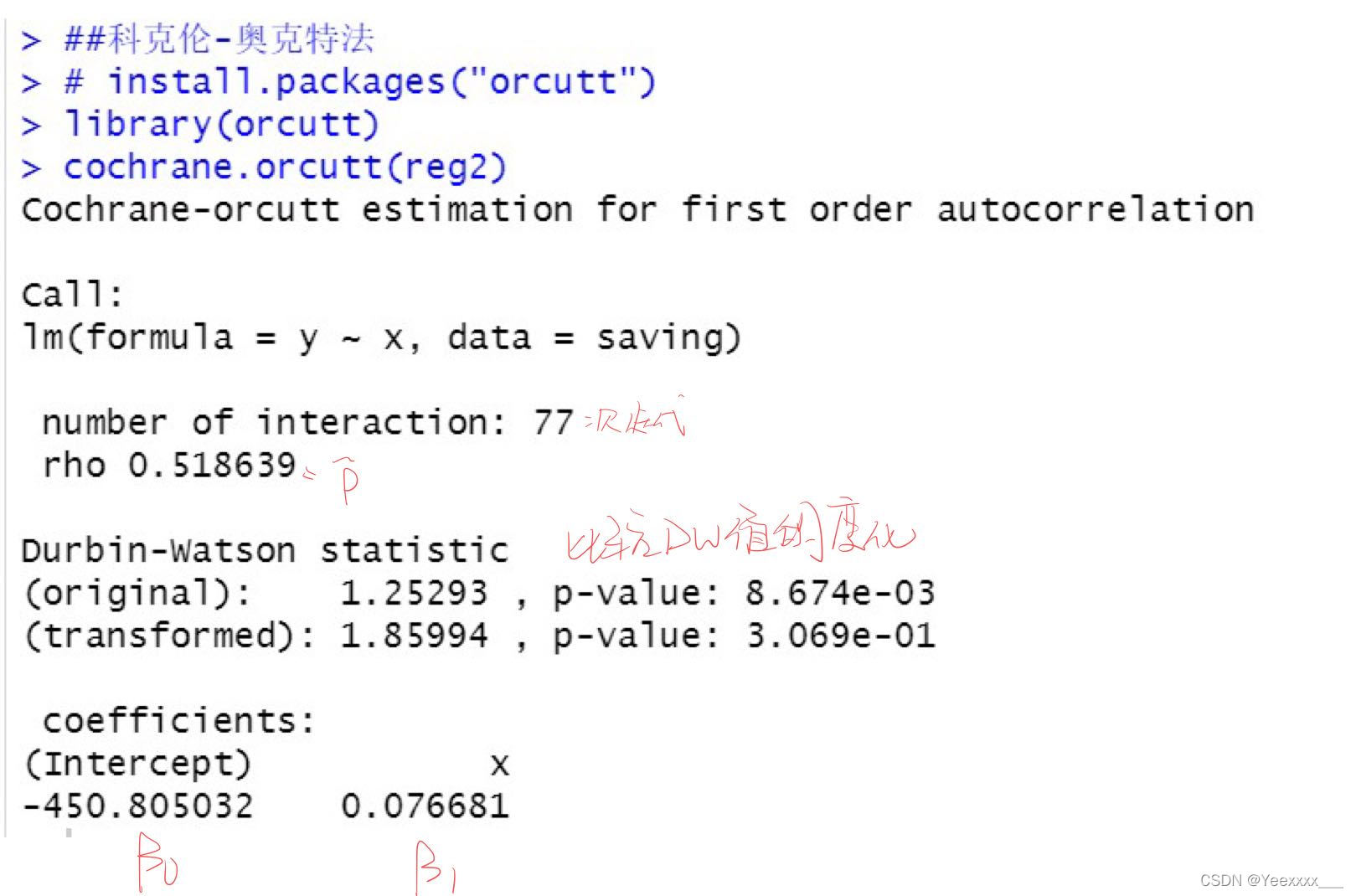
自相關係數的估計值為0.37355，說明誤差項存在中度自相關.

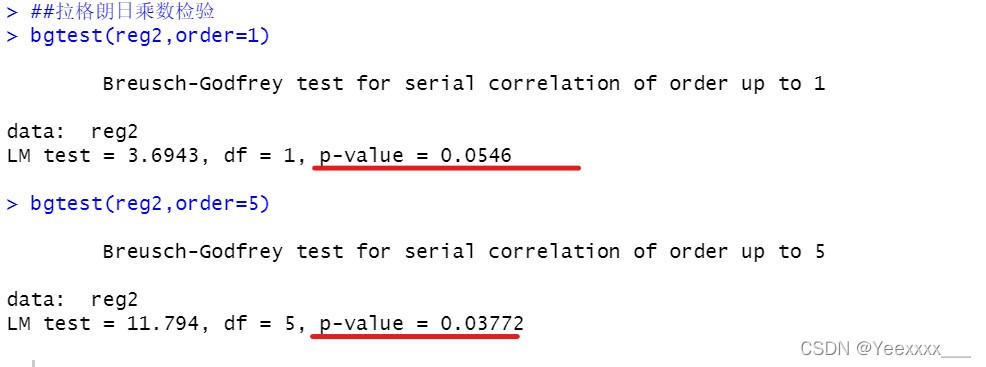
拉格朗日乘數檢驗：order是需要檢驗的階數
在這裡插入圖片描述
顯著性水平 $\alpha =0.05$
$o r d e r = 1$ 時， $p - v a l u e = 0.0546$ ，因為 $\alpha$ ，不能拒絕原假設，認為這個模型不存在顯著的一階自相關.
$o r d e r = 5$ 時， $p - v a l u e = 0.03772$ ，因為 $\alpha$ ，拒絕原假設，認為這個模型存在顯著的五階自相關.

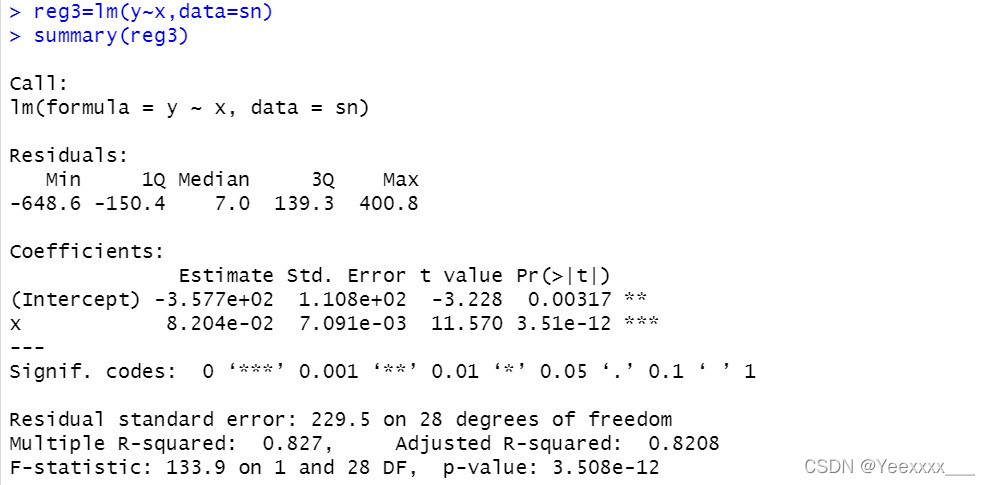
通過廣義差分法消除自相關性：只適用於一階自相關
在這裡插入圖片描述

通過科克倫-奧克特迭代法消除自相關性：只適用於二階及以上的高階自相關
在這裡插入圖片描述
code：

saving=read.table("eg5.8_ch5.txt",header=T)
reg2=lm(y~x,data=saving)

##DW檢驗(lmtest包)
dwtest(reg2)
rho=1-0.5* 1.2529; rho  # DW = 2(1-rho自相關係數)

##拉格朗日乘數檢驗
bgtest(reg2,order=1)
bgtest(reg2,order=5)

##廣義差分
n=nrow(saving)
st=saving[-1,]
stlag1=saving[1:(n-1),]
sn=st-rho*stlag1  # DW
cbind(st,stlag1,sn)  # 二三列滯後一期 最後兩列廣義差分
reg3=lm(y~x,data=sn)
summary(reg3)

##科克倫-奧克特法
# install.packages("orcutt")
library(orcutt)
cochrane.orcutt(reg2)

例四多重共線性診斷

在這裡插入圖片描述
相關係數矩陣直觀診斷：

從相關係數矩陣中可以看出解釋變數中至少存在兩組顯著的負線性相關.
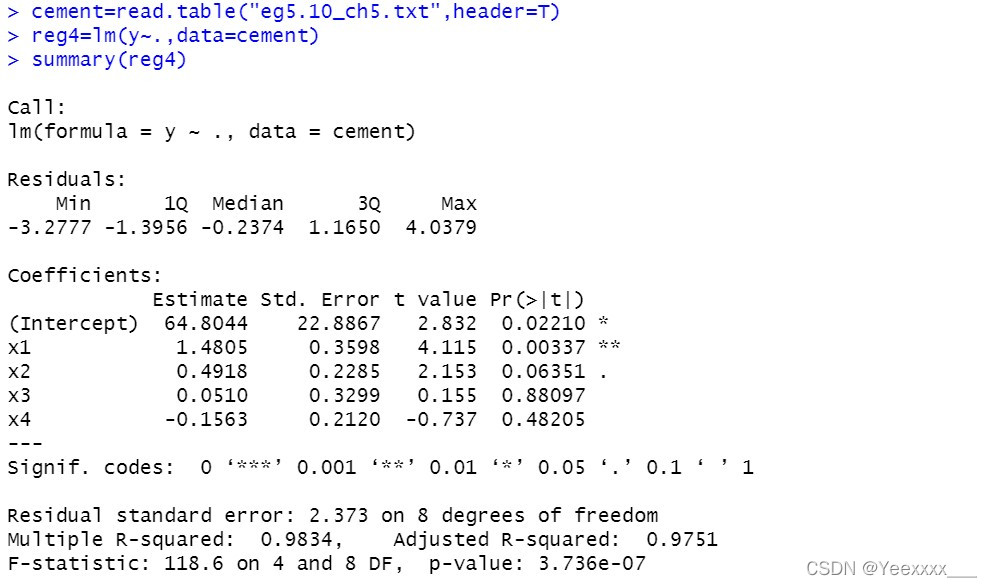
迴歸診斷：
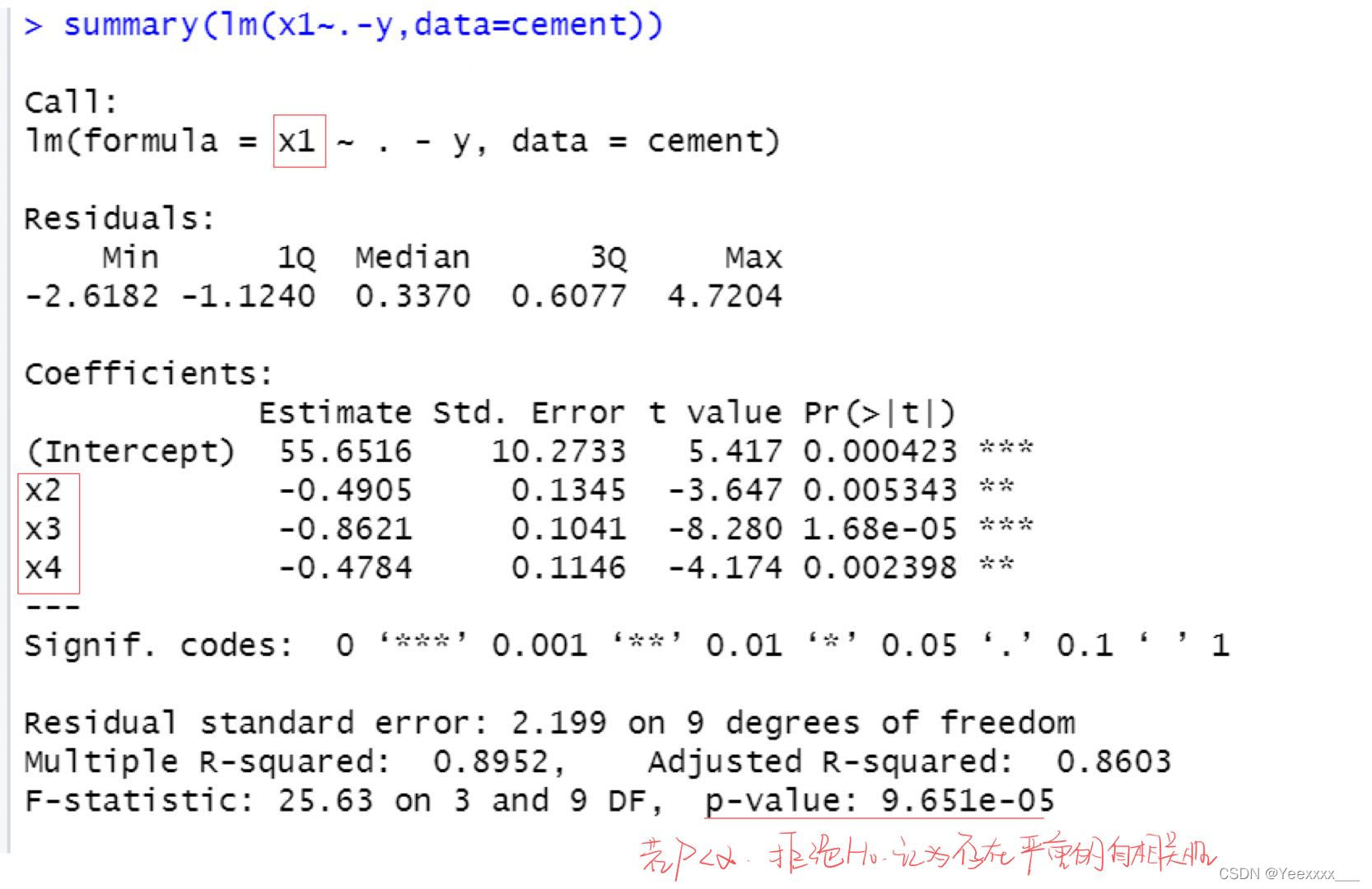
在這裡插入圖片描述
這裡只做了 $x_1$ 與其餘解釋變數的輔助迴歸方程，其他可以自己試.

方差膨脹因子診斷：
在這裡插入圖片描述
判斷方法一:一般方差膨脹因子大於10，認為存在嚴重的多重共線性. 所以上述結果說明存在兩組嚴重的多重共線性.
判斷方法二:四個vif的平均值大於1，說明存在嚴重的多重共線性.

特徵根與條件數診斷法：
在這裡插入圖片描述
至少存在一個特徵根近似為0時，則解釋變數之間必存在多重共線性.
條件數大於100時認為存在嚴重的多重共線性.

code：

cement=read.table("eg5.10_ch5.txt",header=T)
reg4=lm(y~.,data=cement)
summary(reg4)

cor(cement)
summary(lm(x1~.-y,data=cement))

##VIF
# install.packages('DAAG')
library(DAAG)
vif(reg4,digit=3)


##特徵根和條件數
xx=as.matrix(cbind(1,cement[,1:4]))
pho=cor(t(xx)%*%(xx)); pho
eigen(pho)
kappa(pho,exact=TRUE)

多元線性迴歸模型的各種診斷