---

一、棧(Stack)

1.棧的基本概念

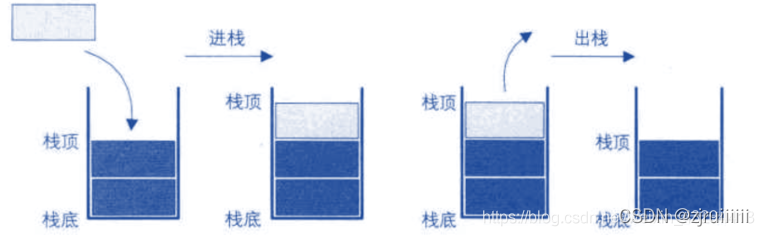
棧：一種特殊的線性表，其只允許在固定的一端進行插入和刪除元素操作。進行資料插入和刪除操作的一端稱為棧頂，另一端稱為棧底。棧中的資料元素遵守後進先出LIFO（Last In First Out）的原則。

壓棧：棧的插入操作叫做進棧/壓棧/入棧，入資料在棧頂。
出棧：棧的刪除操作叫做出棧。出資料在棧頂。

棧頂指標：顧名思義，棧頂指標是指向棧頂的一個指標。但Java當中沒有指標這一說法，因此也可以當作下標來進行處理。

需要注意的是：棧頂指標指向的是可以存放元素的棧的位置，一旦有元素放入後它再加1。

Stack中的方法有：

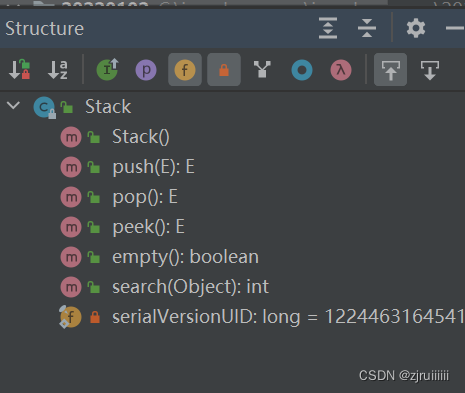
push為壓棧，pop為出棧（返回值為出棧的值），peek為棧頂元素，empty為判斷棧是否為空，search為找出某個元素在棧中的第幾個位置，返回下標。

2.用順序表實現棧

用順序表實現的棧稱為順序棧，只是該順序表的實際操作也是一樣要遵循棧的基本操作——先進後出。

public class MyStack {
    private int[] elem ;
    private int top = 0 ;

    public MyStack() {
        this.elem = new int[3];
    }

    public void push(int item) {
        if(top==elem.length) {
            Arrays.copyOf(elem,5);
            return;
        }
        elem[top]=item;
        top++;
    }
    public int pop() {
        if(top==0) {
            throw new UnsupportedOperationException("棧為空");
        }
        top--;
        int ret = this.elem[top];
        return ret;
    }
    public int peek() {
        if(top==0) {
            throw new UnsupportedOperationException("棧為空");
        }
        return this.elem[top-1];
    }
    public int search(int item) {
        return 0;
    }
}

3.用連結串列實現棧

**用連結串列實現棧要注意一個點：因為棧遵循的是先進後出，因此我們在入棧時的操作為單連結串列的頭插法，出棧時的操作為刪除單連結串列的頭結點，並使得頭結點指向下一結點。**只有這樣用單連結串列實現棧才能做到時間複雜度為O(1)。

class Node{
    public int val;
    public Node next;

    public Node(int val) {
        this.val = val;
    }
}
public class MyLinkedStack {
    public Node head;
    public void push(int data) {
        Node node = new Node(data);
        if(head==null) {
            head=node;
        } else {
            node.next=head;
            head=node;
        }
    }
    public int pop() {
        int ret = head.val;
        head=head.next;
        return ret;
    }
    public void display() {
        Node cur = head;
        while(cur!=null) {
            System.out.print(cur.val+" ");
            cur=cur.next;
        }
    }
}

4.有關棧的相關面試題

例一：不可能的輸出序列

題目：一個棧的入棧序列是a,b,c,d,e則棧的不可能的輸出序列是：（）
A edcbd B decba C dceab D abcde

解：答案為C，一定要時刻注意棧的特點：先進後出。分析B選項。因為第一個出棧為d，則直接入棧到d後停止，d出棧。還剩a,b,c；第二個出棧為c，則還剩a，b；第三個出棧為e，則我們可以令e入棧後再出，此時還是剩a，b；再將b，a出棧則為b選項。D選項則是每一個進棧後直接先出。

例二：中綴表示式轉字尾表示式

題目：將中綴表示式轉為字尾表示式，如中綴表示式X = a+b * c-d，則其字尾表示式為？

解：因為是一個表示式，先用括號將整體括起來(X = a+b * c-d)。又因為從左到右運算時，先運算的是乘，將b * c用括號括起來，則為(X=a+(b * c)-d)；接著是用bc的結果去加a，將a與它用括號括起來，則為(X=(a+(bc))-d)；最後再計算減d，結果為(X=((a+(b * c))-d))。再將運運算元移到相應右括號的外面再將括號去掉，最終得字尾表示式為Xabc * +d-= 。

例三：有效的括號

對應leetcode題

思路：因為題目的要求是括號是否匹配，將左括號（包括左大括號、左中括號、左小括號）壓入棧中，如果不是左括號，則與棧頂的左括號進行匹配，‘(‘ 對應 ‘)’；‘[’d對應’]’；‘{’對應‘}’。否則返回false。

此題有四種情況：
1.左括號和右括號相等的情況下，左括號與右括號出現了不匹配的情況，返回false。
2.左括號多於右括號不可能匹配成功，現象為遍歷字串結束後棧中還有元素。
3.右括號多於左括號也不可能匹配成功，現象為當遍歷到右括號時棧中沒有元素跟其進行配對。
4.左括號與右括號都配對成功，並且遍歷完字串後棧中沒有元素。

例如"{[]}"字串，首先初始化一個棧，將‘{’壓入棧中，下一個為‘[’，是左括號壓入棧中。下一個為‘]’，與棧中的第一個元素進行配對，發現為‘[’，則將棧頂元素出棧。下一個為‘}’，與棧中的元素‘{’匹配成功，最後字串遍歷完成並棧中沒有元素，返回true。

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        int i = 0;
        while(i<s.length()) {
            if(s.charAt(i)=='('||s.charAt(i)=='{'||s.charAt(i)=='[') {
                stack.push(s.charAt(i));
            }else {
                char ch = s.charAt(i);
                if(ch==')') {
                    if(!stack.empty()&&stack.peek()=='(') {
                        stack.pop();
                    } else {
                        return false;
                    }
                } else if(ch=='}') {
                    if(!stack.empty()&&stack.peek()=='{') {
                        stack.pop();
                    }else {
                        return false;
                    }
                } else if(ch==']') {
                    if(!stack.empty()&&stack.peek()=='[') {
                        stack.pop();
                    }else {
                        return false;
                    }
                }
            }
            i++;
        }
        if(stack.empty()) {
            return true;
        }
        return false;
    }
}

例四：最小棧

對應leetcode題

思路：初始化兩個棧，一個為stack普通棧，另一個為minStack專門用來存放每次壓入棧stack中的最小值。
1、當一個元素要壓入stack中（push方法），則minStack是否要壓入棧有兩種情況：(1)當minStack為空時，直接將該元素壓入minStack中即可。(2)當minStack不為空，則需要與minStack中的棧頂元素進行比較，如果小於或等於minStack棧頂元素，則壓入minStack中；否則無需壓入minStack。
2、當一個元素要從stack中出棧（pop方法），則minStack對應的處理：如果stack中出棧的元素與minStack的棧頂元素相同，它們對應棧中的最小值，minStack中的棧頂元素也要出棧。
3、minStack中的棧頂元素就是stack中全部元素的最小值。

class MinStack {
    private Stack<Integer> stack ;
    private Stack<Integer> minStack;
    public MinStack() {
        stack=new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(minStack.empty()) {
            minStack.push(val);
        }else {
            int top = minStack.peek();
            if(top>=val) {
                minStack.push(val);
            }
        }
    }
    
    public void pop() {
        if(stack.empty()) {
            return;
        }
        int top = stack.pop();
        if(top==minStack.peek()) {
            minStack.pop();
        }
    }
    
    public int top() {
        if(stack.empty()) {
            return -1;
        }
        return stack.peek();
    }
    
    public int getMin() {
        if(minStack.empty()) {
            return -1;
        }
        return minStack.peek();
    }
}

二、佇列(Queue)

1.佇列的基本概念

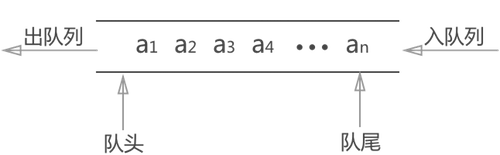
只允許在一端進行插入資料操作，在另一端進行刪除資料操作的特殊線性表，佇列具有先進先出FIFO(First In First Out) 。入佇列：進行插入操作的一端稱為隊尾（Tail/Rear） 。出佇列：進行刪除操作的一端稱為隊頭（Head/Front）。

Queue介面中的方法：

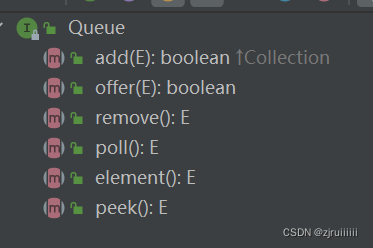
add和offer方法沒什麼大致的區別，都是入隊操作。remove為刪除某一個元素（但是它不太符合佇列的特點，因此比較少用）。poll為出隊操作，並且返回的是出隊時的元素。element和peek都為獲得隊頭的元素，但對對頭不進行操作。

Queue

錯誤處理	丟擲異常	返回特殊值
入佇列	add(e)	offer(e)
出佇列	remove()	poll()
隊首元素	element()	peek()

Deque(雙端佇列)其實也是用連結串列實現。操作不同

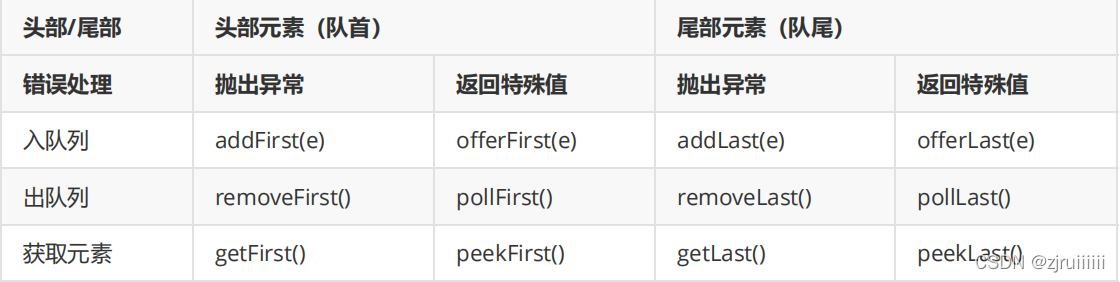
2.用連結串列實現佇列

為何不用順序表實現佇列是因為用佇列是遵循先進先出原則的，這樣的話在順序表當中很容易造成「假的」滿佇列。即佇列當中沒有任何元素並且front和rear都指向了順序表的最後一個位置就不能再放入元素。為了避免這種情況發生，順序表只能在每次模仿佇列的出隊時，表頭元素出順序表則後面的元素都要向前挪一個單位，這樣時間複雜度就達到了O(n)。

連結串列來實現佇列能做到入隊和出隊的時間複雜度為O(1)，即出隊操作：在表尾處設定last結點，當有元素入隊時last結點指向該新結點，再將last結點改為新結點處。入隊操作：在表頭處設定head結點，當有元素出隊時head指向它的下一個結點。

圖解：
1、初始連結串列

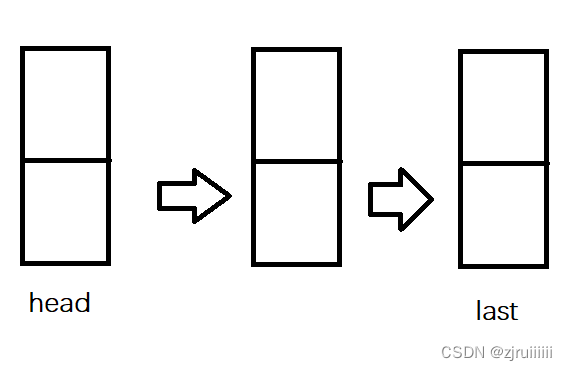
2、入隊

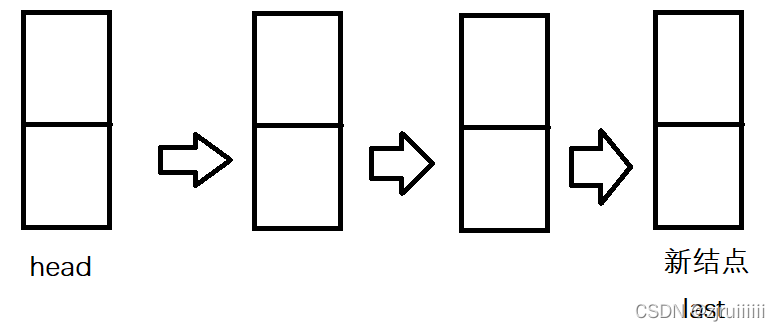
3、出隊

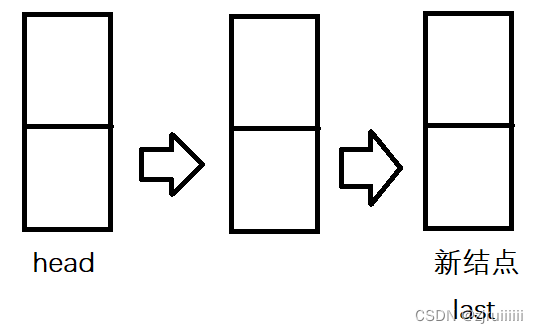
程式碼：

class Node {
    public int val;
    public Node next;

    public Node(int val) {
        this.val = val;
    }
}
public class MyLinkedQueue {
    public Node first;
    public Node last;

    public void offer(int data) {
        Node node = new Node(data);
        if(first==null) {
            first=node;
            last=node;
            return;
        }
        last.next=node;
        last=node;
    }
    public int poll() {
        if(first==null) {
            throw new UnsupportedOperationException("佇列為空");
        }
        int ret = first.val;
        first=first.next;
        return ret;
    }
    public boolean isEmpty() {
        if(first==null) {
            return true;
        }
        return false;
    }
    public int remove() {
        if(first==null) {
            return -1;
        }
        int ret = first.val;
        first=first.next;
        return ret;
    }
    public int peak() {
        if(first==null) {
            throw new UnsupportedOperationException("佇列為空");
        }
        int ret = first.val;
        return ret;
    }
}

3.有關佇列的面試題

例一：用佇列實現棧

對應leetcode題

思路：題目給出要用兩個佇列實現棧。因此我們可以先初始化兩個佇列que1和que2。重點和難點是要在兩個佇列的出隊或入隊的操作中實現棧的先進後出原則。

1、push方法：如果是一開始兩個佇列均為空，則入隊的元素任選一個隊入隊即可；當不是第一次入隊，則入隊的元素選擇在不為空的隊當中入。則結果肯定是有一個隊有元素，而另一個隊為空隊。
2、pop方法：因為棧的特點是後進先出，即後入隊的要先出隊，則我們可以把有元素的隊的隊長減1個元素直接入隊到另一條隊中，還剩下的那一個元素不再入隊，直接poll即可。
3、top方法：跟pop的操作方法類似，只是將一個隊當中的全部元素入到另一個隊當中，並且返回的是最後一個入隊的元素。
4.empty方法：如果兩個佇列均為空，則棧為空，返回true。

圖解：
1、初始化兩個佇列

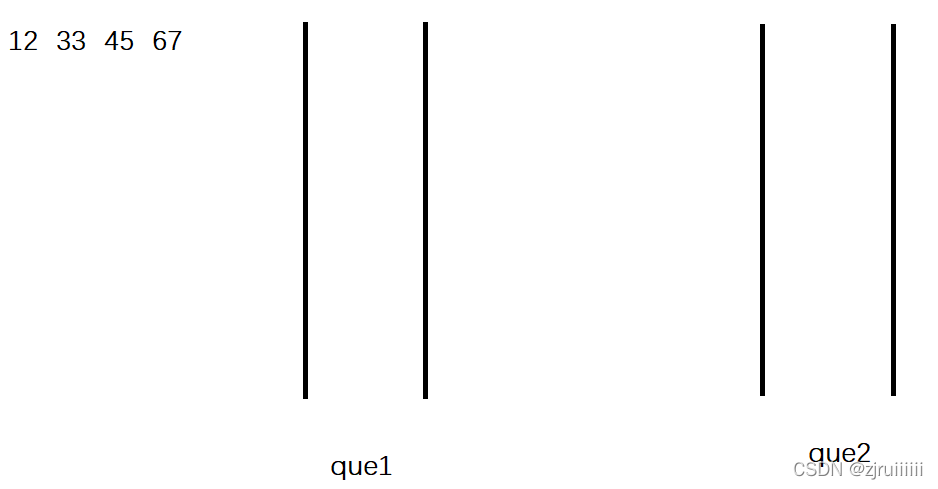
2、入棧（假設入12、33和45）

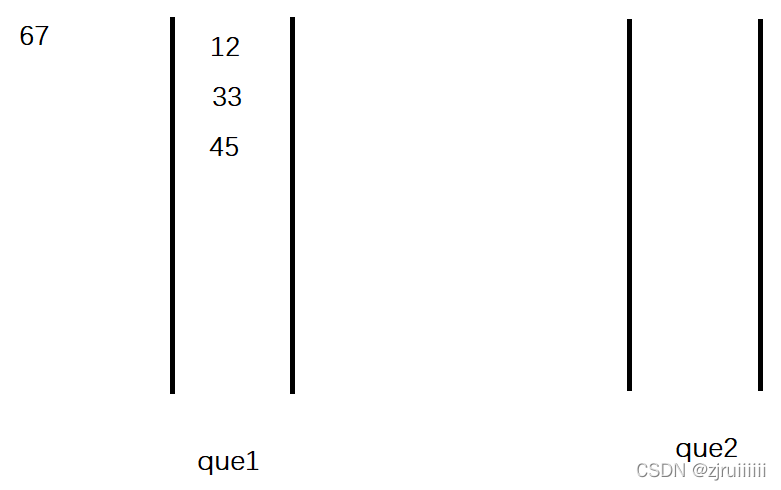
3、出棧（假設出45）

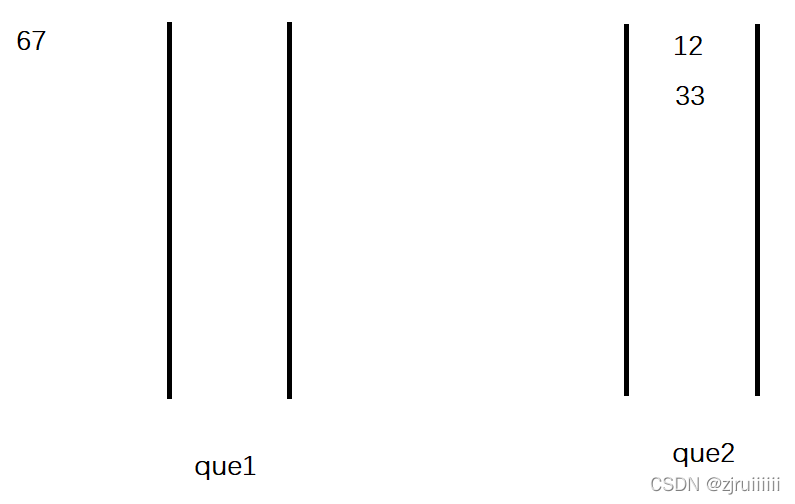
4、入棧（入67）

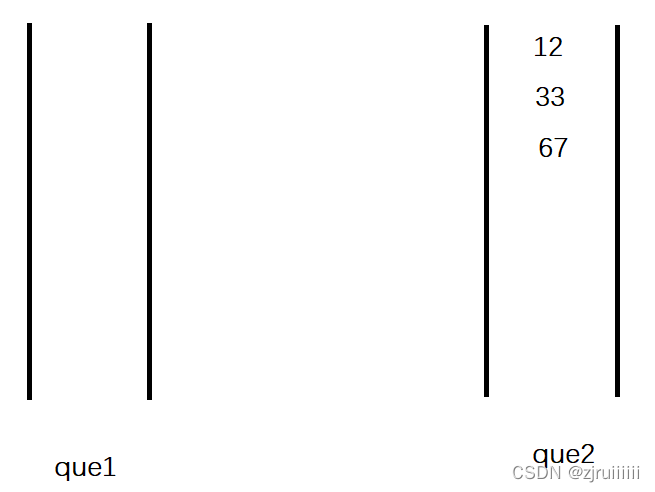
大概的操作就這麼多。以此類推。

class MyStack {
    private Queue<Integer> que1;
    private Queue<Integer> que2;
    public MyStack() {
        que1=new LinkedList<>();
        que2=new LinkedList<>();
    }
    
    public void push(int x) {
        if(!que1.isEmpty()) {
            que1.offer(x);
        }else if(!que2.isEmpty()) {
            que2.offer(x);
        }else {
            que1.offer(x);
        }
    }
    
    public int pop() {
        if(empty()) {
            return -1;
        }else {
            if(!que1.isEmpty()) {
                int size = que1.size();
                int i=0;
                while(i<size-1) {
                    que2.offer(que1.poll());
                    i++;
                }
                return que1.poll();
            }else{
                int size = que2.size();
                int i=0;
                while(i<size-1) {
                    que1.offer(que2.poll());
                    i++;
                }
                return que2.poll();
            }
        }
    }
    
    public int top() {
        if(empty()) {
            return -1;
        }else {
            if(!que1.isEmpty()) {
                int size = que1.size();
                int i=0;
                int x=-1;
                while(i<size) {
                    x = que1.poll();
                    que2.offer(x);
                    i++;
                }
                return x;
            }else{
                int size = que2.size();
                int i=0;
                int x = -1;
                while(i<size) {
                    x=que2.poll();
                    que1.offer(x);
                    i++;
                }
                return x;
            }
        }
    }
    
    public boolean empty() {
        return que1.isEmpty()&&que2.isEmpty();
    }
}

注意：Queue是一個介面，不可以直接初始化。它的介面內部沒有size方法，但它是繼承與Collection的（Collection介面有size方法），並且此處參照的是子類LinkedList物件，則重寫了size方法。

例二：用棧實現佇列

對應leetcode題

思路：題目要求用兩個棧來實現佇列，即要用棧來實現先進先出原則。先初始化兩個棧stack1和stack2。一個棧只能進行push，另一個只能進行pop。

1、push方法：只能在其中一個棧當中入棧，此處令stack1只能進行入棧操作，則當有元素要push時直接壓入stack1中。
2、pop方法：此處令stack2只能進行出棧操作，如果stack1和stack2為空則無法再出棧。若stack1有元素而stack2為空，則將stack1中的元素全部壓入stack2中，再將stack2中的棧頂元素出棧，則能夠模仿出隊操作。若stack2已經不為空了，則直接將棧頂元素出棧即可。
3、peek方法：stack2當中的棧頂元素等同於佇列的隊頭元素，若stack2為空則同為pop方法的操作將stack1中的棧元素全部壓入stack2中，再取stack2中的棧頂元素。
4、empty方法：若兩個棧都為空，則模仿的佇列為空，返回true。

圖解：
1、壓隊（先將12，33，45入隊）

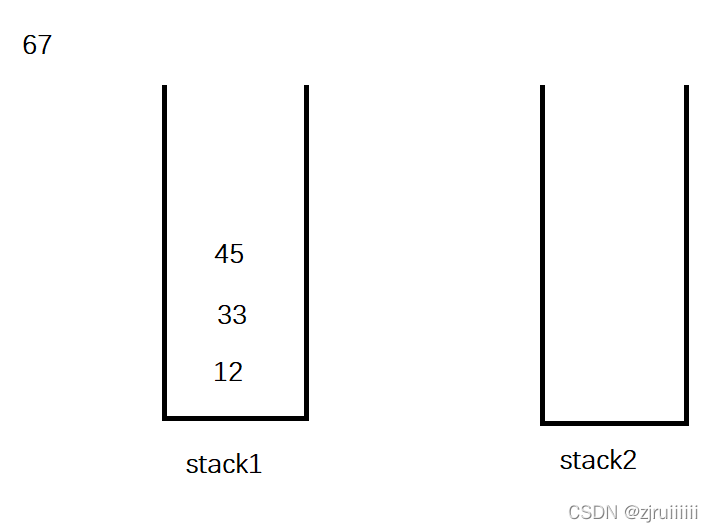
2、出隊（將12出隊）

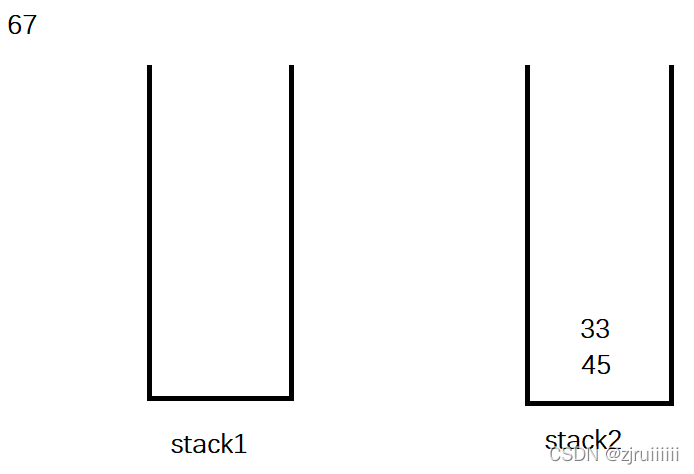
3、取隊頭元素：就是stack2中的棧頂元素。

class MyQueue {
    Stack<Integer> stack1 ;
    Stack<Integer> stack2 ;
    public MyQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }
    
    public void push(int x) {
        stack1.push(x);
    }
    
    public int pop() {
        if(empty()) {
            return -1;
        }
        if(stack2.empty()){
            while(!stack1.empty()) {
                int x = stack1.pop();
                stack2.push(x);
            }
        }
        return stack2.pop();
    }
    
    public int peek() {
        if(empty()) {
            return -1;
        }
        if(stack2.empty()){
            while(!stack1.empty()) {
                int x = stack1.pop();
                stack2.push(x);
            }
        }
        return stack2.peek();
    }
    
    public boolean empty() {
        return stack1.empty()&&stack2.empty();
    }
}

例三：設計迴圈佇列

對應leetcode題

思路：佇列的底層是一個陣列,設其為elem，設計迴圈佇列能夠避免佇列的"假滿"情況，我們可以設定front（指向隊頭元素）和rear（指向在隊尾可以放的元素）兩個座標來操作迴圈連結串列。

設計迴圈連結串列需要的知識：
1、front和rear初始化的值都為0，代表迴圈佇列為空。

2、front和rear每當有元素出隊或有元素入隊時的下一個下標為front=(front+1)%elem.length或rear=(rear+1)%elem.length。

3、front和rear開始的時候都置為0，但是會有一種情況出現。我們假設elem陣列的長度為8，則最後一個下標為7。假設沒有任何元素出隊，則front一直指向0下標。當rear指向下標為7的元素時，該元素再入隊後經公式計算得rear指向的下標為0，此時front和rear相等，那麼隊滿和隊空的判斷條件就衝突了。因此我們可以浪費最後一個元素的位置來判斷隊空還是隊滿。

4、當我們取隊尾元素的時候，不能想當然地直接去取rear-1的元素。因為rear也有可能會在下標為0的位置出。因此只要判斷rear是否在0位置處，如果是則直接返回的是elem.length-1的下標位置，否則就可以指向rear-1的下標的元素。

5、因為我們要浪費最後一個下標的空間來判斷迴圈佇列是滿還是空，因此假設陣列的長度為k，我們只能放k-1個元素，但是leetcode中的迴圈佇列要求你初始化多長的陣列就要放多少個元素。則在初始化陣列的時候加個1即可。

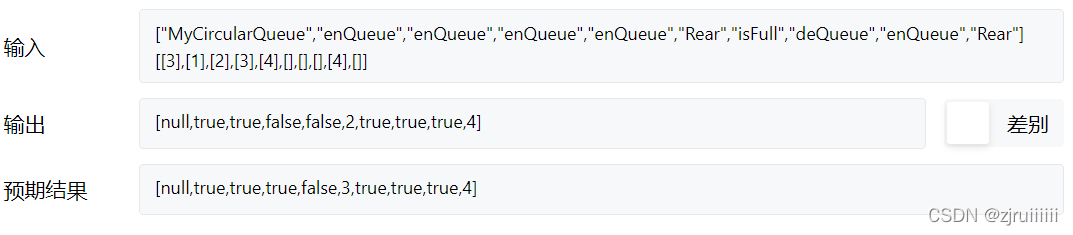
程式碼：

class MyCircularQueue {
    private int[] elem ;
    private int front ;
    private int rear;
    public MyCircularQueue(int k) {
        elem=new int[k+1];
        front=0;
        rear=0;
    }
    
    public boolean enQueue(int value) {
        if(isFull()) {
            return false;
        }
        elem[rear]=value;
        rear=(rear+1)%elem.length;
        return true;
    }
    
    public boolean deQueue() {
        if(isEmpty()) {
            return false;
        }
        front=(front+1)%elem.length;
        return true;
    }
    
    public int Front() {
        if(isEmpty()) {
            return -1;
        }
        return elem[front];
    }
    
    public int Rear() {
        if(isEmpty()) {
            return -1;
        }
        int index = (rear==0)?elem.length-1:rear-1;
        return elem[index];
    }
    
    public boolean isEmpty() {
        if(rear==front) {
            return true;
        }
        return false;
    }
    
    public boolean isFull() {
        if((rear+1)%elem.length==front) {
            return true;
        }
        return false;
    }
}

如果覺得這篇文章對你受益匪淺，麻煩點個贊支援一下謝謝！