基於多分類線性SVM&mediapipe手勢關鍵點實現簡易人機猜拳遊戲

在【機器學習演演算法】支援向量機入門教學及相關數學推導 這篇部落格中，我們已經完整的推導了SVM演演算法以及SMO序列最小化優化演演算法的來龍去脈。在本篇部落格中，我們將基於這些理論基礎，手寫程式碼實現SVM演演算法的完整實現過程。並基於分類結果進行資料+決策面的視覺化；同時，填一下上上上上上篇部落格挖的坑，實現一個有趣的小應用：上次是基於邏輯斯蒂迴歸，這次我們用SVM演演算法來進行手勢識別。

本次實驗的所有程式碼已上傳至github：https://github.com/Scienthusiasts/Machine-Learning
先貼一張實現效果：

基於SMO優化的SVM分類演演算法完整實現版本

本次手寫程式碼的主要理論基礎在【機器學習演演算法】支援向量機入門教學及相關數學推導中都有比較詳盡的解釋，推薦這兩篇部落格可以對照著看，相信對大家一定會有不一樣的體會與理解。🎈

首先，我們構造一個類來實現SVM演演算法，類中包括演演算法的超引數，待優化的模型引數，以及模型用到的訓練樣本等：

class SVM:
    def __init__(self, X, y, C, ε, ker):
        self.X = X                # 資料集
        self.y = y                # 標籤
        self.C = C                # 鬆弛變數在損失中的權重
        self.ε = ε                # 容忍一定的誤差
        self.m = X.shape[0]       # X總數
        self.α = np.zeros((self.m, 1)) # 待求解引數α
        self.b = 0     # 待求解引數b
        self.ker = ker # 核函數引數
        # eCache儲存每個引數的誤差E，第一列為是否有效的標誌位(是否計算過而不是初始的0)
        self.eCache = np.zeros((self.m, 2)) 

然後，SVM一個必不可少的通過樣本的高維對映實現非線性劃分的方法就是引入核函數。

核函數的種類有許多，在本例中我們採用最簡單和常用的兩種：線性核和高斯核

    # 核函數
    def K(self, xi, xj, param=0):
        # 線性核函數
        if param == 0:
            xj = xj.reshape(-1, 1)
            return np.dot(xi, xj)
        # 高斯核函數
        if param == 1: 
            σ = 1.3 # 核函數的方差σ是一個超引數
            deltaRow = xi - xj
            ker = np.exp(-np.dot(deltaRow, deltaRow.T) / (2 * σ * σ))
            return ker

在SMO優化過程中，為了更新後的α2能用更新前的α2表示，而不是不夠直觀的ζ，我們需要用到標籤與模型預測結果之間的差值E。同時，啟發式搜尋αj也需要用到E。

因此我們需要定義一個方法來實現對E的求解：

    # 計算誤差Ek
    def calcEk(self, k):
        # 計算SVM模型的預測結果：
        fk = np.sum([self.α[i] * self.y[i] * self.K(self.X[i,:], self.X[k,:], self.ker) for i in range(self.m)]) + self.b
        # 計算誤差:
        Ek = fk.reshape(1) - self.y[k]
        return Ek

由於我們定義了一個誤差快取eCache來記錄這些誤差，因此順便實現一個誤差更新方法：

    # 更新第k個引數的誤差
    def updateEk(self, k):
        # 計算誤差
        Ek = self.calcEk(k)
        # 更新計算後的誤差
        self.eCache[k,0] = 1
        self.eCache[k,1] = Ek

在SMO選取引數αj的過程中，使用的是基於誤差E最小的啟發式的方法，這裡定義一個方法實現：

    # 隨機選取第二個引數, 不同於i即可
    def selectJRand(self, i, m):
        j = i
        while(j==i):
            j = int(random.uniform(0, m))
        return j
    
    # 啟發式選取第j個引數, 更高效
    def selectJ(self, i, Ei):
        bestJ = -1     # 最佳誤差對應第幾個α 
        maxDeltaE = 0  # 記錄最大誤差|Ei - Ej|
        Ej = 0         # 記錄最佳引數αj對應的誤差Ej
        # 獲取那些已經更新過的Ek(非0)
        validE = np.nonzero(self.eCache[0,:])[0]
        if len(validE) > 1:
            # 遍歷那些已經計算過的Ei，選擇其中最大的對於的αj作為第二個引數
            for k in validE:
                # j和i不能是同一個
                if k == i: continue
                # 計算當前alpha的E
                Ek = self.calcEk(k)
                # 兩個差值要最大
                deltaE = abs(Ei - Ek)
                if deltaE > maxDeltaE:
                    bestJ = k
                    maxDeltaE = deltaE
                    Ej = Ek
            return bestJ, Ej
        else:   # 對於第一次更新的情況，Ek還沒更新過
            j = self.selectJRand(i, self.m)
            Ej = self.calcEk(j)
        return j, Ej

在SMO求得αj的值後，由於約束條件的存在，我們還需要對違背約束條件的αj進行截斷：

    # 根據約束條件約束求得的α(矩形+線性區域)
    def clipAlpha(self, αj, H, L):
        if αj > H:
            αj = H
        if αj < L:
            αj = L
        return αj

在定義了一些零零碎碎但是必不可少的方法後，接下來就是對基於一次迭代的SMO優化演演算法流程的完整實現(更新一對引數)：

   # SMO優化演演算法流程:
    def innerL(self, i):
        # 計算誤差
        Ei = self.calcEk(i)
        # K.K.T.條件  (ε是一個很小的數，容忍一些誤差？)
        # (1) αi = 0     =>  yi(wTxi + b) - 1 > 0 + ε 【非支援向量】
        # (2) 0 < αi < C =>  yi(wTxi + b) - 1 = 0     【支援向量】
        # (3) αi = C     =>  yi(wTxi + b) - 1 ≤ 0 - ε 【內嵌向量】

        # 啟發式尋找引數i(如果滿足K.K.T.條件直接跳過)：
        # if語句用來判斷是否違法了K.K.T.條件(3)(1):
        if ((self.y[i]*Ei < -self.ε) and (self.α[i] < self.C)) or ((self.y[i]*Ei > self.ε) and (self.α[i] > 0)):
            # 啟發式尋找引數j：
            j, Ej = self.selectJ(i, Ei)
            old_αi, old_αj = self.α[i].copy(), self.α[j].copy()

            # 先求好這三個引數，之後會用到
            K11 = self.K(self.X[i,:], self.X[i,:], self.ker)
            K12 = self.K(self.X[i,:], self.X[j,:], self.ker)
            K22 = self.K(self.X[j,:], self.X[j,:], self.ker)

            # αi 和 αj 的解帶有約束:
            # (1) αiyi + αjyj = ζ
            # (2) 0 < αi,j < C
            # 分情況求解待約束的解：
            if self.y[i] != self.y[j]:
                L = max(0, self.α[j] - self.α[i])
                H = min(self.C, self.C + self.α[j] - self.α[i])
            else:
                L = max(0, self.α[j] + self.α[i] - self.C)
                H = min(self.C, self.α[j] + self.α[i])
            
            # 列印一些優化時的引數資訊
            # L == H的情況是αj正好在矩形約束對角線的點上
            # 若 L = H，αj = L = H
            if(L == H): print("出現 L = H = %f, i = %d, j = %d, αj=%f" %(L, i, j, self.α[j])); return 0
            η = -2.0 * K12 + K11 + K22
            # 若 η <= 0，就無需優化了？？？
            if η <= 0: print("η <= 0"); return 0
            # 若 η >= 0,有更新公式：
            self.α[j] += self.y[j] * (Ei - Ej) / η
            # 約束α的範圍
            self.α[j] = self.clipAlpha(self.α[j], H, L)
            # 更新αj的誤差
            self.updateEk(j)
            if(np.abs(self.α[j] - old_αj) < 1e-5):
                print("j 更新的太少")
                return 0
            # 更新αi
            self.α[i] += self.y[i] * self.y[j] * (old_αj - self.α[j])
            # 接下來求解引數b:
            D_αi, D_αj = (self.α[i] - old_αi), (self.α[j] - old_αj)
            b1 = - Ei - self.y[i] * K11 * D_αi - self.y[j] * K12 * D_αj + self.b
            b2 = - Ej - self.y[i] * K12 * D_αi - self.y[j] * K22 * D_αj + self.b
            # 分情況更新引數b：
            if 0 < self.α[i] < self.C: self.b = b1
            elif 0 < self.α[j] < self.C: self.b = b2
            else: self.b = (b1 + b2) / 2.0
            return 1
        else: return 0

啟發式的尋找αi，將innerL(self, i)寫在迭代流中，並實時輸出迭代更新的引數資訊；模型收斂或達到最大迭代次數後退出。我們將這一過程封裝成訓練方法：

    # 訓練流程，基於SMO演演算法
    def train(self, maxIter):
        iter = 0 # 記錄迭代次數
        entireSet = True 
        αPairsChanged = 0
        # 當迭代次數超過最大迭代次數或任何α都無需優化時(收斂), 退出
        while(iter < maxIter) and ((αPairsChanged > 0) or (entireSet)):
            αPairsChanged = 0
            if entireSet:
                print("===========================全資料集遍歷===========================")
                # 遍歷針對所有向量
                for i in range(self.m):
                    # 選取αij並更新
                    αPairsChanged += self.innerL(i)
                    print("Iteration:%d | choosed i=%d | 已更新的引數對數:%d" % (iter, i, αPairsChanged))
                iter += 1
                # print("已優化所有引數，演演算法提前結束！")
                # break
            else: 
                print("===========================非邊界值遍歷===========================")
                # 僅遍歷非邊界向量
                nonBoundIs = np.nonzero((self.α>0) * (self.α<self.C))[0]
                # 遍歷非邊界值
                for i in nonBoundIs:
                    αPairsChanged += self.innerL(i)
                    print("Iteration:%d | choosed i=%d | 已更新的引數對數:%d" % (iter, i, αPairsChanged))
                iter += 1
            # 遍歷一次後改為非邊界遍歷
            if entireSet: 
                entireSet = False
            # 如果alpha沒有更新，計算全樣本遍歷
            elif (αPairsChanged == 0):
                entireSet = True

        if(iter >= maxIter):print("超過最大迭代次數，演演算法結束")
        if not((αPairsChanged < 0) or (entireSet)):print("演演算法收斂")

        # 對於線性核:
        if(self.ker == 0):
            self.W = np.zeros((self.X.shape[1], 1))
            for i in range(self.m):
                self.W += self.α[i] * self.y[i] * self.X[i,:].reshape(-1,1)
            return self.W, self.b
        # 對於非線性核:
        return self.b, self.α

在模型訓練完畢後，可以儲存模型權重以便離線使用：

值得注意的是，能夠使用引數W和b的模型僅限於線性SVM(或線性核)，對於非線性SVM而言，由於核函數已經將樣本X對映到了高維空間，因此我們只能基於引數α，訓練集X， b進行模型的推理，而不能基於原始的樣本特徵。由於訓練集X涉及的樣本量可能很大，因此本篇部落格中我們暫不考慮基於預訓練非線性SVM的推理實現。

    # 儲存權重(線性核)
    def save_weight_lin(self, path):
        weight = np.concatenate((self.W, self.b.reshape(-1,1)), axis=0)
        np.save(path, weight)

同樣，模型的預測(評估驗證集)也可以分為兩種推理方式，基於W和b的線性SVM，基於α，訓練集X， b的非線性SVM：

    # 測試
    # 核心公式就是 y = wTx + b
    # 在超平面上方時為y>0,為類別1
    # 在超平面下方時為y<0,為類別-1
    def eval(self, test_X):
        res = []
        sv_index = np.nonzero(self.α)[0]
        for j in range(test_X.shape[0]):
            res.append(self.b + np.sum([self.α[i] * self.y[i] * self.K(self.X[i,:], test_X[j,:], self.ker) for i in sv_index]))
        return np.array(res)

    # 對於線性核，直接採用y = wTx + b判別方法，避免計算需要使用X(對映到高維空間的核資料不行)
    @staticmethod
    def linear_eval(test_X, W, b):
        res = b + np.dot(test_X, W)
        return res

SVM決策結果與資料集視覺化

在書《機器學習實戰》中，一共提供了兩個例子供我們實驗。一個好處是，這些資料是二維的，因此我們可以先視覺化看看這些資料的分佈特徵：

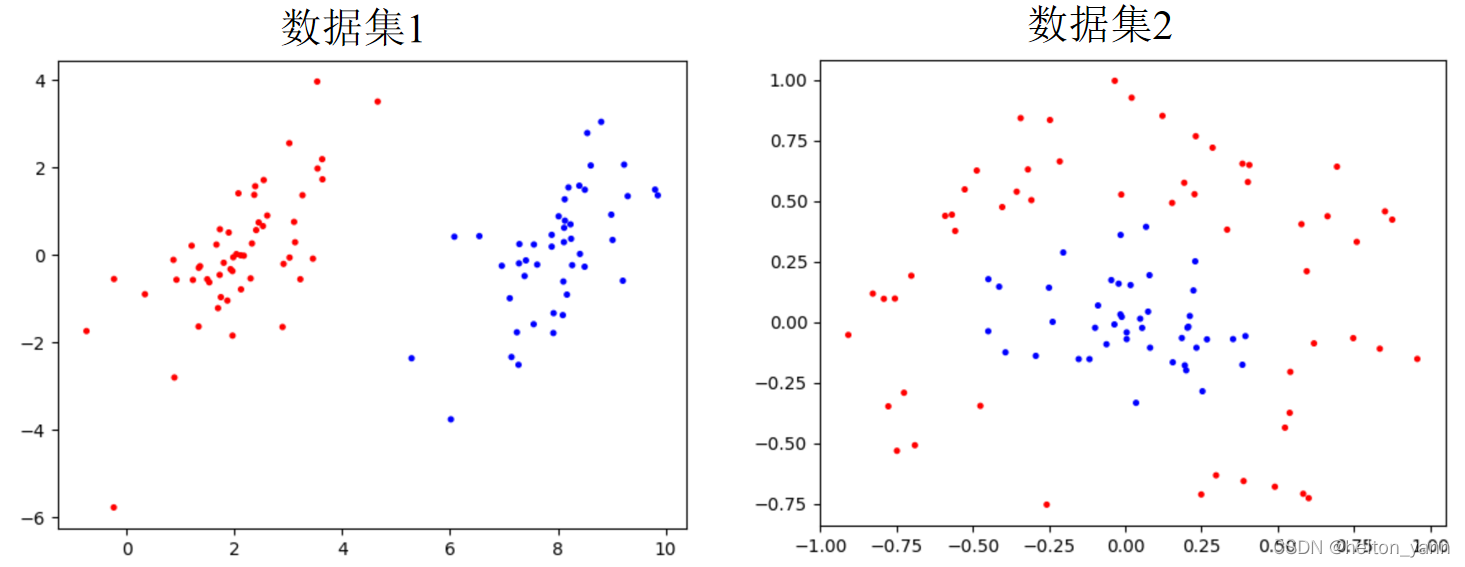
顯而易見，資料集1是線性可分的，資料集2是線性不可分的。對於線性可分的資料，採用線性SVM就可以完美的解決問題，對於那些線性不可分的資料，我們需要利用核對映來解決。

測試程式碼：

if __name__ == '__main__':
    kernelType = 0

    # 讀取資料(txt)
    X, y = loadDataSet('./testSet.txt')
    y = y.reshape(-1,1)
    # visualDataSets2D(X, y)

    svm = SVM( X, y, C=0.6, ε=1e-4, ker=kernelType)
    _, b, α = svm.train(maxIter=1)
    print(α)
    # 測試
    res = svm.eval(X)
    acc = sum(res*y>0) / X.shape[0]
    # print("準確率: %f" % (acc))
    visualModel2D(X, y, b, α, kernelType)

視覺化模型決策結果(資料集1，線性SVM)：

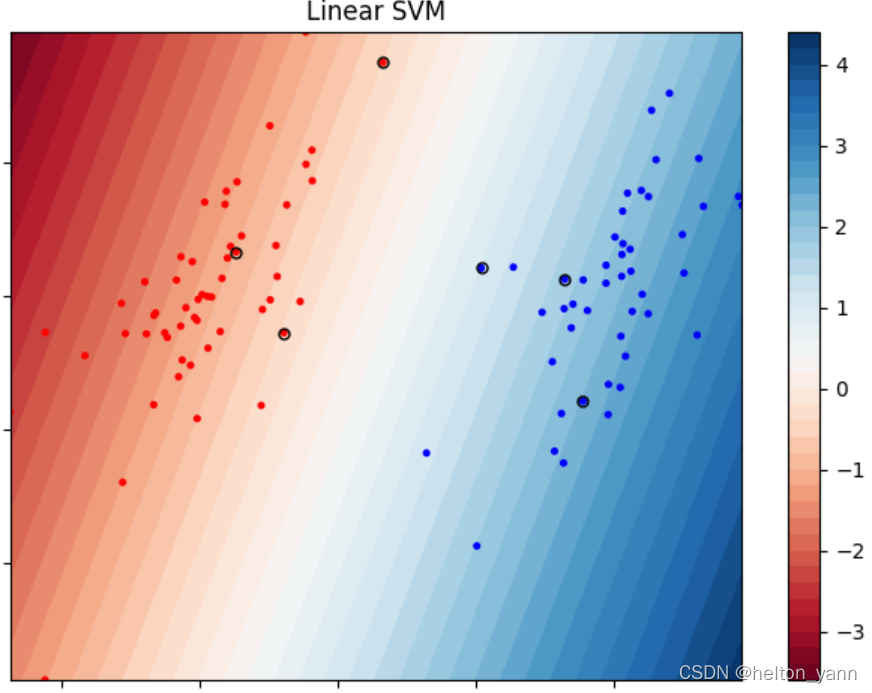
圖中圈起來的點代表支援向量，值得注意的是，基於軟間隔SVM的支援向量不一定恰好都落在間隔邊界上，這是因為軟間隔SVM具有一定的容錯力，也就是說，最大間隔可能嵌入在樣本之中(總之模型肯定會幫助你找到一條最優直線，這條直線是容錯率與模型泛化能力的tradeoff)

【但是說實話我還是不太理解為什麼線性SVM的支援向量沒有恰好在一條直線上，或許是和鬆弛變數有關。。🐶】

… …

Iteration:0 | choosed i=97 | 已更新的引數對數:4
Iteration:0 | choosed i=98 | 已更新的引數對數:4
Iteration:0 | choosed i=99 | 已更新的引數對數:4
超過最大迭代次數，演演算法結束
演演算法收斂
準確率: 1.000000
支援向量個數： 6

對於資料集2而言，可以使用高斯核來引入非線性SVM。

視覺化模型決策結果(資料集2，非線性SVM)：

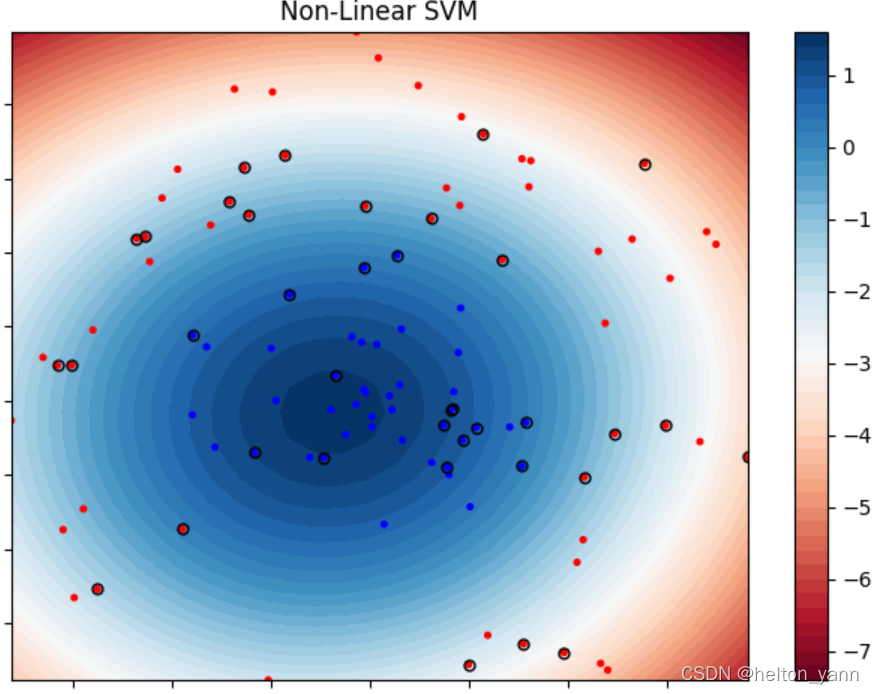
Iteration:0 | choosed i=94 | 已更新的引數對數:26
Iteration:0 | choosed i=97 | 已更新的引數對數:27
Iteration:0 | choosed i=98 | 已更新的引數對數:27
出現 L = H = 0.000000, i = 99, j = 53, αj=0.000000
Iteration:0 | choosed i=99 | 已更新的引數對數:27
超過最大迭代次數，演演算法結束
演演算法收斂
準確率: 0.990000
支援向量個數： 37

一般而言，對於線性可分的資料，在其任意高維的某個特徵空間中都一定是線性可分的，因此我們可以對資料集1引入高斯核：

視覺化模型決策結果(資料集1，非線性SVM)：

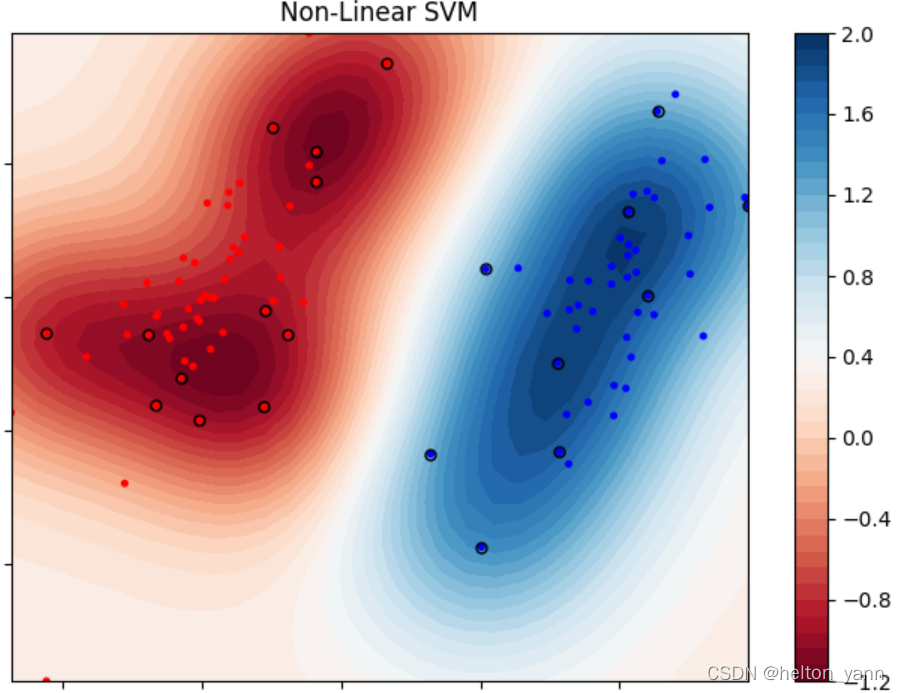
Iteration:0 | choosed i=98 | 已更新的引數對數:15
出現 L = H = 0.000000, i = 99, j = 85, αj=0.000000
Iteration:0 | choosed i=99 | 已更新的引數對數:15
超過最大迭代次數，演演算法結束
演演算法收斂
準確率: 0.990000
支援向量個數： 21

多分類SVM實戰：基於mediapipe手勢關鍵點實現簡易版人機猜拳

在上一節機器學習實戰中，我們利用邏輯斯蒂迴歸演演算法實現了二分類手勢識別。在本節中，我們將核心演演算法改為線性SVM，實現手勢三分類。具體的資料採集方法以及如何使用mediapipe工具包在上一次部落格中已經有了詳細的說明，感興趣的小夥伴可以點選傳送門：【機器學習實驗四】基於Logistic Regression二分類演演算法實現手部姿態識別

二分類演演算法如何實現多分類

SVM和邏輯斯蒂迴歸演演算法有一個相同點，那就是它們都只能執行二分類任務，要實現對於兩個以上類別的多分類，我們可以採取一些特殊的方法：

1. OVO(one versus one)

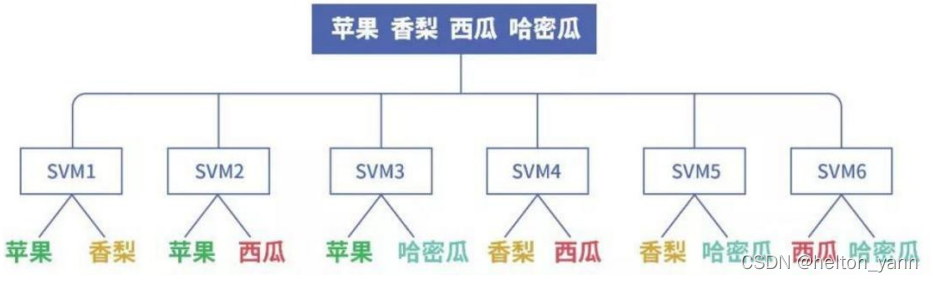
ovo即一對一的方法，我們可以將多個類別兩兩組合，假設有n個類別，兩兩組合就能產生n(n-1)/2個資料集，這時候我們需要對每對組合的資料集訓練一個模型，總共訓練n(n-1)/2個模型。在每次預測時，採用投票的方式選擇預測類別最多的那個類別作為最終的預測結果。

基於ovo訓練方法的缺點在於，一旦資料類別一多，需要訓練的模型的個數將以平方級別增長，因此這種方法適用於小類別下的簡單資料集。

下面這張圖很直觀的表達了ovo資料集劃分方法：

2.OVR(one versus rest)

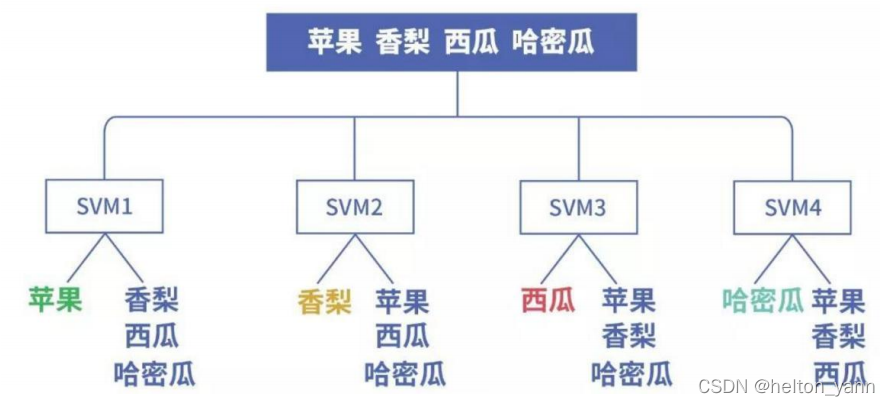
ovr即一對多方法，在資料劃分時依次將某個類別的樣本歸為正例而其餘的樣本歸為負例。假設有n個類別，我們就需要訓練n個模型。在每次預測時，選擇唯一分為正例的模型對應的類別作為最終預測結果。如果同時有多個模型預測出正例，則選取期望值最大的那個(對於SVM就是數值>0且越大越好)

基於ovr訓練方法的缺點也比較明顯，那就是正負例的樣本很有可能分佈不均衡，負例的樣本數通常比較大。

下面這張圖很直觀的表達了ovr資料集劃分方法：

基於OVO方法訓練三分類SVM

在本次實戰中，我們選擇OVO方法進行資料劃分，一共需要訓練三個模型，即三組權重。

首先需要將三個類別的資料兩兩組合，分成三個資料集：

    # # 匯入資料集(手勢關鍵點)
    cloth_X = np.load("./cloth_dist.npy")
    stone_X = np.load("./stone_dist.npy")
    scissors_X = np.load("./scissors_dist.npy")
    y = np.ones(cloth_X.shape[0])
    # one versus one 
    X0  = np.concatenate((cloth_X,stone_X), axis=0).reshape(-1,21*21)
    X1  = np.concatenate((cloth_X,scissors_X), axis=0).reshape(-1,21*21)
    X2  = np.concatenate((stone_X,scissors_X), axis=0).reshape(-1,21*21)
    y  = np.concatenate((y,-y), axis=0).reshape(-1,1)
    # three mixed together 
    X012 = np.concatenate((X0,scissors_X.reshape(-1,21*21)), axis=0).reshape(-1,21*21)
    y012 = np.concatenate((np.zeros(cloth_X.shape[0]),np.ones(cloth_X.shape[0])), axis=0)
    y012 = np.concatenate((y012,np.ones(cloth_X.shape[0])*2), axis=0)
    print(X012.shape, y012.shape)

(1500, 441) (1500,)

然後，對每個資料集訓練一組權重：

    kernelType = 0
    Xs = {0:X0, 1:X1, 2:X2}
    for i in Xs.keys():
        svm = SVM( Xs[i], y, C=600, ε=1e-4, ker=kernelType)
        W, b = svm.train(maxIter=1)
        svm.save_weight_lin('./W&b_'+str(i)+'.npy')

驗證精度：

    # 測試(三個模型)
    res0 = svm.linear_eval(X012, W0, b0).reshape(-1)>0
    res1 = svm.linear_eval(X012, W1, b1).reshape(-1)>0
    res2 = svm.linear_eval(X012, W2, b2).reshape(-1)>0

    # 三分類
    pred = []
    for i in range(len(res0)):
        if(res0[i] and res1[i]):pred.append(0)
        elif(not res0[i] and res2[i]):pred.append(1)
        elif(not res1[i] and not res2[i]):pred.append(2)
        else:pred.append(-1)

    acc = sum(pred==y012) / X012.shape[0]
    print("準確率: %f" % (acc))

準確率: 0.998000

測試(嵌入mediapipe手部關鍵點提取程式碼中)

如何實現人機互動式猜拳呢，哈哈其實很簡單，只需要將模型識別手勢的類別改為相剋的屬性即可🤣🤣

在程式碼首嵌入以下內容：

cls = {0:img2, 1:img0, 2:img1}
clstext1 = {0:"Paper", 1:"Rock", 2:"Scissors"}
clstext2 = {0:"Scissors", 1:"Paper", 2:"Rock"}
# 讀取SVM權重
weight0 = np.load('./W&b_0.npy')
W0, b0 = weight0[:-1], weight0[-1]
weight1 = np.load('./W&b_1.npy')
W1, b1 = weight1[:-1], weight1[-1]
weight2 = np.load('./W&b_2.npy')
W2, b2 = weight2[:-1], weight2[-1]

def eval(X):
  # 測試(三個模型)
  res0 = SVM.linear_eval(X, W0, b0).reshape(-1)>0
  res1 = SVM.linear_eval(X, W1, b1).reshape(-1)>0
  res2 = SVM.linear_eval(X, W2, b2).reshape(-1)>0

  if(res0 and res1):pred = 0
  elif(not res0 and res2):pred = 1
  elif(not res1 and not res2):pred = 2
  else:pred = -1
  return pred

其中cls = {0:img2, 1:img0, 2:img1}用來選擇三張圖片用來表示計算機方的選擇(石頭，剪刀，布)：

在手部關鍵點提取程式碼下加上這幾行程式碼即可：

... ... 
from deal_hand_frame import distance
import sys;sys.path.append('../')
from logistic import logistic
... ...  
        X = distance(keypoint.reshape(1,21,3)).reshape(1,-1)
        pred = eval(X)
        w, h,_ = cls[pred].shape
        image[:w, -h:, :] = cls[pred]
        
        cv2.putText(image, 'your:' + clstext1[pred], (10,50), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 0, 255), 2)
        cv2.putText(image, 'computer:' + clstext2[pred], (10,100), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0), 2)
... ...

測試效果展示(贏是不可能贏的)：

在後續改進中，也可以針對兩名人類玩家的對弈實現一個猜拳積分系統。