【Day13】每天三演演算法

題目

NC136 輸出二元樹的右檢視

描述

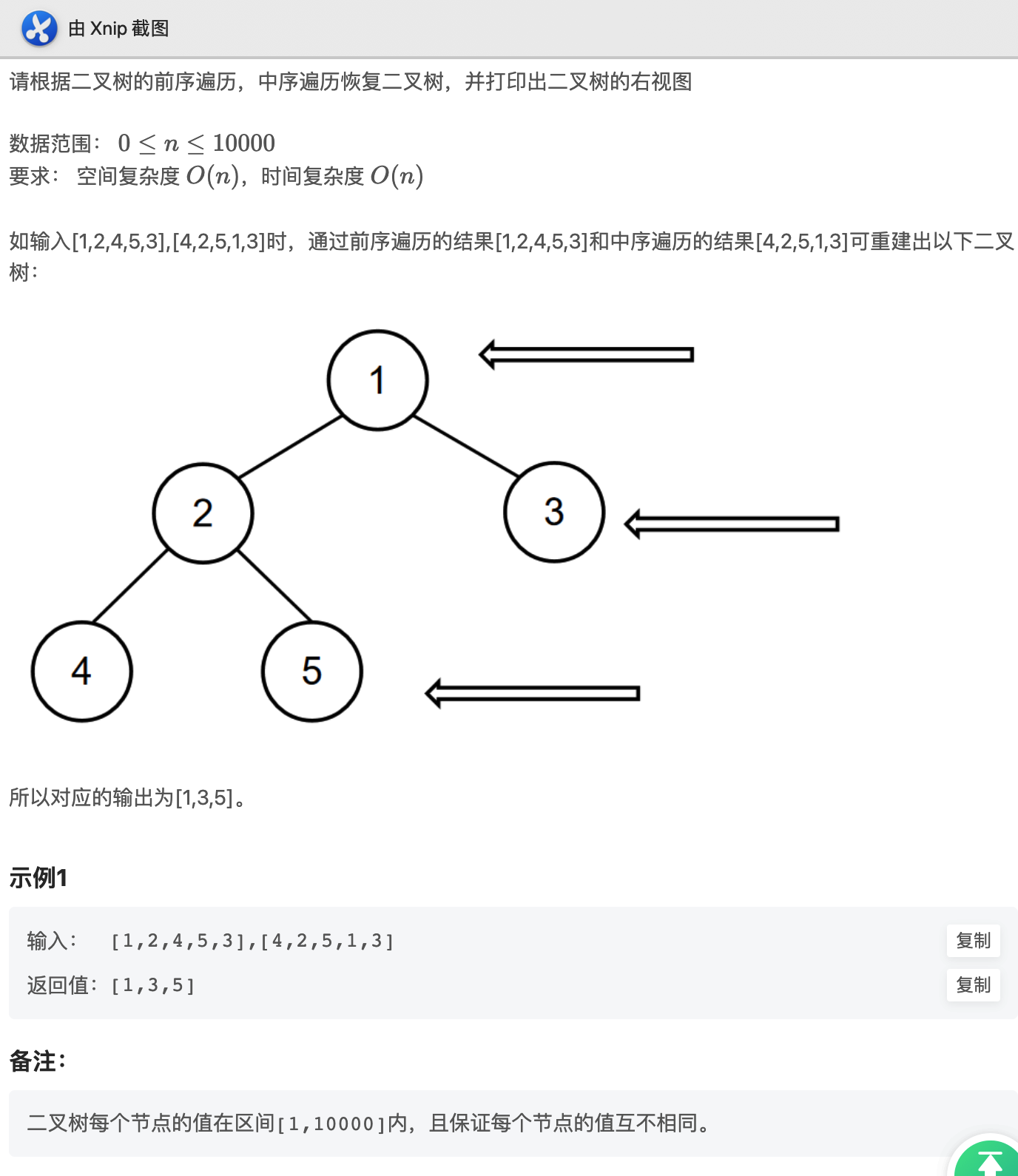
思考

對於這道題，我們有兩步要走

**1、**建樹

**2、**獲取右檢視

建樹這個好說，我們之前做過類似的題目，這裡就不再贅述了

而獲取右檢視，我們可以通過層次遍歷，然後每次去除當前層的最後一個元素即可

題解

• 根據先序和中序構造二元樹

我對 buildTree 方法有封裝了一層，這是編碼的常見操作了，可以理解為我們對其他呼叫者封裝了一層 API，方便後續呼叫

同時，咱們封裝的方法可以對入參進行更好的條件判斷，可謂是一舉多得

public TreeNode buildTree(int[] xianxu, int[] zhongxu) {
  if (xianxu==null || xianxu.length==0) return null;
  return buildTree(xianxu,zhongxu,0,xianxu.length-1,0,zhongxu.length-1);
}

// 構建二元樹
private TreeNode buildTree(int[] xianxu, int[] zhongxu,int xl,int xr,int zl,int zr) {
  if (xl>xr) return null;
  int midVal = xianxu[xl];
  TreeNode root = new TreeNode(midVal);
  // 獲取左邊的長度
  int llen=0;
  for (int i = zl; i <=zr ; i++) {
    if (zhongxu[i]==midVal) {
      llen=i-zl;
      break;
    }
  }
  root.left=buildTree(xianxu,zhongxu,xl+1,xl+llen,zl,zl+llen-1);
  root.right=buildTree(xianxu,zhongxu,xl+llen+1,xr,zl+llen+1,zr);
  return root;
}

• 根據二元樹，獲取右檢視

這裡就是按照我之前的思路，層次遍歷，然後每次獲取每層最後一個元素

public List<Integer> getRightView(TreeNode root) {
  List<Integer> rightView = new ArrayList<>();
  Queue<TreeNode> queue = new LinkedList<>();
  queue.add(root);
  while (!queue.isEmpty()) {
    int size = queue.size();
    for (int i = 0; i < size; i++) {
      TreeNode tmp = queue.poll();
      if (i==size-1) {
        rightView.add(tmp.val);
      }
      if (tmp.left!=null) queue.add(tmp.left);
      if (tmp.right!=null) queue.add(tmp.right);
    }
  }
  return rightView;
}

• 被調函數

我們的根呼叫函數如下

其順序就是先構造二元樹，然後獲取右檢視

public int[] solve (int[] xianxu, int[] zhongxu) {
  if (xianxu.length==0) return new int[0];
  // 只有1個或2個節點的情況下，其右檢視一定是和先序遍歷一樣的
  if (xianxu.length<=2) return xianxu;
  TreeNode root = buildTree(xianxu, zhongxu);
  List<Integer> rightView = getRightView(root);
  int[] res = new int[rightView.size()];
  for (int i = 0; i < res.length; i++) {
    res[i]=rightView.get(i);
  }
  return res;
}

• 完整程式碼如下

public int[] solve (int[] xianxu, int[] zhongxu) {
  if (xianxu.length==0) return new int[0];
  // 只有1個或2個節點的情況下，其右檢視一定是和先序遍歷一樣的
  if (xianxu.length<=2) return xianxu;
  TreeNode root = buildTree(xianxu, zhongxu);
  List<Integer> rightView = getRightView(root);
  int[] res = new int[rightView.size()];
  for (int i = 0; i < res.length; i++) {
    res[i]=rightView.get(i);
  }
  return res;
}

public TreeNode buildTree(int[] xianxu, int[] zhongxu) {
  if (xianxu==null || xianxu.length==0) return null;
  return buildTree(xianxu,zhongxu,0,xianxu.length-1,0,zhongxu.length-1);
}

// 構建二元樹
private TreeNode buildTree(int[] xianxu, int[] zhongxu,int xl,int xr,int zl,int zr) {
  if (xl>xr) return null;
  int midVal = xianxu[xl];
  TreeNode root = new TreeNode(midVal);
  // 獲取左邊的長度
  int llen=0;
  for (int i = zl; i <=zr ; i++) {
    if (zhongxu[i]==midVal) {
      llen=i-zl;
      break;
    }
  }
  root.left=buildTree(xianxu,zhongxu,xl+1,xl+llen,zl,zl+llen-1);
  root.right=buildTree(xianxu,zhongxu,xl+llen+1,xr,zl+llen+1,zr);
  return root;
}


// 層次遍歷，每次獲取每層的最後一個元素
public List<Integer> getRightView(TreeNode root) {
  List<Integer> rightView = new ArrayList<>();
  Queue<TreeNode> queue = new LinkedList<>();
  queue.add(root);
  while (!queue.isEmpty()) {
    int size = queue.size();
    for (int i = 0; i < size; i++) {
      TreeNode tmp = queue.poll();
      if (i==size-1) {
        rightView.add(tmp.val);
      }
      if (tmp.left!=null) queue.add(tmp.left);
      if (tmp.right!=null) queue.add(tmp.right);
    }
  }
  return rightView;
}

小結

這道題在牛客上定級是 medium

其實，就是兩個 easy 題目的綜合

希望各位以後在見到 medium 甚至 hard 的時候，不要慌張，因為，思路往往就在以前做過的題目中

NC109_島嶼數量

描述

思考

這道題，我們可以先考慮遍歷圖形

一旦遇到1，說明我們遇到島嶼，那麼我們可以計數+1，並將這座島嶼弄沉

以此往復，直到遍歷結束

這種方式，也有前人總結出了一個名詞，叫「島嶼沉沒法」

題解

public int solve (char[][] grid) {
  if (grid==null || grid.length==0) return 0;
  int count = 0;
  for (int i = 0; i < grid.length; i++) {
    for (int j = 0; j < grid[0].length; j++) {
      if (grid[i][j]=='1') count++;
      sinkIsland(i,j,grid);
    }
  }
  return count;
}

// 將當前島嶼沉沒
private void sinkIsland(int r,int c,char[][] grid) {
  int R = grid.length;
  int C = grid[0].length;
  if (r<0 || r>=R || c<0 || c>=C) return;
  if (grid[r][c]!='1') return;
  grid[r][c]='0';
  int[] rs = {0,0,1,-1};
  int[] cs = {1,-1,0,0};
  for (int i = 0; i < 4; i++) {
    sinkIsland(r+rs[i],c+cs[i],grid);
  }
}

小結

這道題其實沒啥難度

但是我想考考各位，我這個方法的時間複雜度是多少呢？

我估計有同學可能會說 O(n^3)

答案其實是 O(n^2)

別看有個 二重 for 迴圈 和一個 DFS

其實那個二重 for 迴圈的時間複雜度我們只能算 n，我們的資料是以二維陣列的形式儲存的，其遍歷方式就必須借用到二重 for 迴圈，你總不能把相同量的資料，從二維改為一維儲存，就說遍歷它的時間複雜度變為 O(n) 了把？

如果要再細緻一點，這道題的時間複雜度應該是在 O(n) - O(n^2) 之間

O(n) 即不存在島嶼，O(n^2) 即整張圖都是島嶼

NC13 二元樹的最大深度

描述

思考

這道題是最最經典，也是最容易的 dfs 題目了（也不知道是怎麼混到我的題庫裡的😂）

我們只需對二元樹進行深度遍歷，然後記錄每次到葉子的深度並進行比較即可

題解

public int maxDepth (TreeNode root) {
  if(root==null) return 0;
  return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}

總結

這種 easy 其實沒啥好總結的，我主要是想提一提 dfs 和 bfs 的選擇

BFS 適合找出路這類問題，我們拿迷宮舉例，想想你每次走迷宮的時候，是不是都是先一條道走到黑，發現這條道走不通，再返回之前最後一個岔路口，然後選其他路走的。DFS 就是這個原理，它每次都會嘗試一條道路到盡頭，直到走不了了才會嘗試其他的道路。這樣的好處就是，一旦某條路走通了，那麼剩下的路我們就可以不走了。

BFS 適合最短路徑這類問題，你想象水面上有一個漂浮物，你隨機向水中丟一塊石頭，石頭產生的漣漪撥散開，直到碰到那個漂浮物。BFS 不會說一條道走到黑，因為最短路徑的終點不一定永遠在邊緣，可能就在起點很近的地方。假如我們還是使用 DFS 一條道走到黑的方法，那麼我們可能會多走許多冤枉路。

回到這道題，雖然 DFS 和 BFS 都能解決，並且無論是 DFS 還是 BFS，都是要對所有節點進行遍歷的。但是基於二者的思想，還是選擇 DFS 更為合適。況且 DFS 相比 BFS ，還要少建一個佇列呢。