小波閾值去噪
目錄
1.概念
小波分析即用Mallat塔式演演算法對訊號進行降階分解。該演演算法在每尺度下將訊號分解成近似分量與細節分量。近似分量表示訊號的高尺度,即低頻資訊;細節分量表示訊號的低尺度,即高頻資訊。
對含有噪聲的訊號,噪聲分量的主要能量集中在小波分解的細節分量中。
2.原理
小波閾值去噪的實質為抑制訊號中無用部分、增強有用部分的過程。小波閾值去噪過程為:(1)分解過程,即選定一種小波對訊號進行n層小波分解;(2)閾值處理過程,即對分解的各層係數進行閾值處理,獲得估計小波係數;(3)重構過程,據去噪後的小波係數進行小波重構,獲得去噪後的訊號。
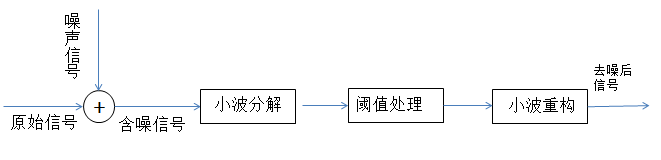
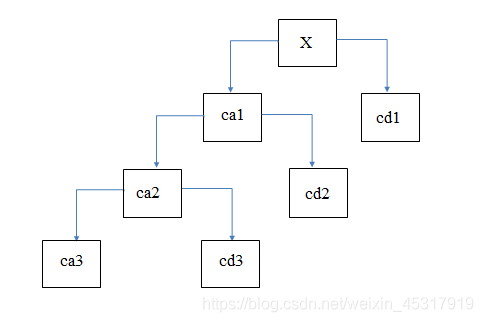
小波分解:X->ca3,cd3,cd2,cd1;小波重構:ca3,cd3,cd2,cd1->X。其中ca為低頻資訊、近似分量,cd為高頻、細節分量。
3.影響降噪效果的因素
3.1小波基的選擇
在對訊號進行小波分解時需要選擇合適的小波基,由於沒有任何一種小波基可以對不同型別的訊號達到最優的分解效果,因此,如何選擇小波基成為小波分解的一個重點。針對現實中的訊號,小波基的選擇一般要考慮以下幾個因素:支撐長度、對稱性、消失矩、正則性、相似性。針對一維訊號,例如語音訊號,通常選擇dB小波和sym小波。
3.2分解層數的選擇
在對訊號進行小波分解時,分解的層數取得越大,則噪聲和訊號表現的不同特性越明顯,越有利於二者的分離,但是分解的層數越大,經過重構的訊號失真也會越大,在一定程度上會對訊號去噪的效果產生較差的影響。因此,如何選擇分解層數以解決信噪分離效果和重構訊號失真之間的矛盾呢?
小波分解的頻段範圍與取樣頻率有關。若進行N層分解,則各個頻段範圍為:

假設原始訊號X的取樣頻率為1000Hz,則訊號的最大頻率為500,對該訊號做3層小波分解,則各個頻段範圍如下圖所示。

3.3閾值的選擇
在小波域,有效訊號對應的係數很大,而噪聲對應的係數很小並且仍滿足高斯分佈。因此可以通過設定閾值將訊號在小波域某段區間內的係數置零,就能最大程度的抑制噪聲,同時只是稍微損傷有效訊號。
閾值選擇規則基於模型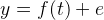 ,
, 是高斯白噪聲。
是高斯白噪聲。
目前常見的閾值選擇方法有:無偏風險估計閾值、極大極小閾值、固定閾值、啟發式閾值。
MATLAB自帶的自適應閾值選擇函數,呼叫格式如下:
thr=thselect(X,str);
根據字串str定義的閾值選擇方法求訊號X的自適應閾值thr。
str= 'rigrsure':無偏風險估計閾值;
str= 'minimaxi':極大極小閾值;
str= 'sqtwolog':固定閾值;
str= 'heursure':啟發式閾值。

一般來講,極大極小閾值和無偏風險估計閾值比較保守,當噪聲在訊號的高頻段分佈較少時,這兩種閾值估計方法效果較好,可以將微弱的訊號提取出來。而固定閾值和啟發式閾值去噪比較徹底,在去噪時顯得更為有效,但是也容易把有用的訊號誤認為噪聲去掉。
3.4閾值函數的選擇
在確定了高斯白噪聲在小波域的閾值門限之後,就需要有個閾值函數對含有噪聲係數的小波係數進行過濾,去除高斯噪聲係數,常用的閾值函數有硬閾值函數和軟閾值函數。
3.4.1硬閾值函數
當小波係數的絕對值大於給定閾值時,小波係數不變;小於閾值時,小波係數置零。
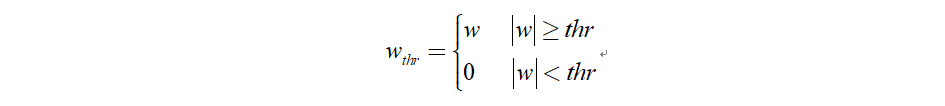
3.4.2軟閾值函數
當小波係數的絕對值大於給定閾值時,令小波係數減去閾值;小於閾值時,小波係數置零。
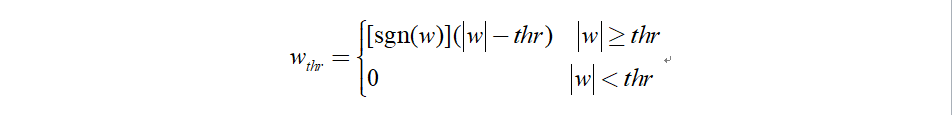
MATLAB自帶的閾值處理常式,呼叫格式如下:
Y=wthresh(X,SORH,thr);
返回輸入向量或矩陣X經過軟閾值(SORH=’s’)或硬閾值(SORH=’h’)處理後的訊號Y,thr是閾值。
4.MATLAB程式碼
%% 基於小波變換的閾值去噪
clc;
clear;
close all;
tic;
%% 用db8小波對含噪訊號進行5層分解並提取係數
[c,l]=wavedec(y,5,'db8'); % y為含噪訊號
%取第5層低頻近似係數
ca5=appcoef(c,l,'db8',5);
%取各層高頻細節係數
cd5=detcoef(c,l,5);
cd4=detcoef(c,l,4);
cd3=detcoef(c,l,3);
cd2=detcoef(c,l,2);
cd1=detcoef(c,l,1);
%% 閾值獲取
% [thr,sorh,keepapp]=ddencmp('den','wv',y); % 函數ddencmp用於獲取訊號在消噪或壓縮過程中的預設閾值
thr=thselect(y,'rigrsure'); % 自適應閾值選擇使用Stein的無偏風險估計原理
% thr=thselect(y,'heursure'); % 使用啟發式閾值選擇
% thr=thselect(y,'sqtwolog'); % 閾值等於sqrt(2*log(length(X)))
% thr=thselect(y,'minimaxi'); % 用極大極小原理選擇閾值
%% 進行硬閾值處理
yhard5=wthresh(cd5,'h',thr);
yhard4=wthresh(cd4,'h',thr);
yhard3=wthresh(cd3,'h',thr);
yhard2=wthresh(cd2,'h',thr);
yhard1=wthresh(cd1,'h',thr);
c1=[ca5;yhard5;yhard4;yhard3;yhard2;yhard1];
y1=waverec(c1,l,'db8');
%% 進行軟閾值處理
ysoft5=wthresh(cd5,'s',thr);
ysoft4=wthresh(cd4,'s',thr);
ysoft3=wthresh(cd3,'s',thr);
ysoft2=wthresh(cd2,'s',thr);
ysoft1=wthresh(cd1,'s',thr);
c2=[ca5;ysoft5;ysoft4;ysoft3;ysoft2;ysoft1];
y2=waverec(c2,l,'db8');
%% 對上述訊號進行圖示
figure(1);
plot(y);title('含噪訊號');
axis tight;
figure(2);
plot(y1);title('硬閾值處理'); %降噪訊號時域圖
axis tight;
figure(3);
plot(y2);title('軟閾值處理'); %降噪訊號時域圖
axis tight;
fs=50;N=4000; % 取樣頻率為50MHz,取樣點數為4000
figure(4);
[f1(:,1),A1(:,1)]=PinPu(y1,fs,N);
plot(f1(:,1),A1(:,1));
title('硬閾值處理');legend('D denoise Signal'); %降噪訊號頻譜圖
axis tight;
figure(5);
[f2(:,1),A2(:,1)]=PinPu(y2,fs,N);
plot(f2(:,1),A2(:,1));
title('軟閾值處理');legend('D denoise Signal'); %降噪訊號頻譜圖
axis tight;
toc;
參考文獻
[1]司莉,畢貴紅,魏永剛等.基於RQA與SVM的聲發射訊號檢測識別方法[J].振動與衝擊,2016,35(2):98.