一本通提高篇 區間類動態規劃

$2020.6.21$考完月考的第一天還沒出成績 趕緊來加一篇$dp$
$2020.10.13$沒報上$CSP$要考聯賽得用老師的推薦名額，所以趕緊回來好好學兩個月拿個一等獎
現在就啥對聯賽有用就學啥，先弄$dp$，再弄圖論，最後整點數奆結垢和數學
先可簡單的整吧

基本概念

大家應該都知道線性$dp$，即線上性結構上進行狀態轉移，而區間類動態規劃是線性動態規劃的拓展，它在分階段劃分問題時，與階段中元素出現的順序和由前一階段哪些元素合併而來有很大的關係。如狀態$f[i][j]$，它表示以 已合併的次數為階段， 以 區卷左端點$i$為狀態，它的值取決於第$i$個元素和第$j$個元素斷開的位置$k$，即$f[i][k]+f[k+1][j]$的值。這一型別的動態規劃，階段特徵得長明顯，求最優值時需要預先設定階段內的區間統計值，還要以動態規劃的起始位置來判斷。

操作

區間$dp$一般只有兩步操作
$1.$合併：即將兩個或多個部分進行整合，當然也可以反過來，也就是對一個問題分解成兩個或多個部分
$2.$求解：對整個問題設最優值，列舉合併點，將問題分解成左右兩個部分，最後合併左右兩個部分得最優值得到原問題的最優值。類似分治演演算法的思想。

所以一個問題能不能用區間$dp$，就是要看這個問題是否能被分解成為兩兩合併的形式。

這塊也沒啥難的 直接上題

石子合併

題面
$Solution:$這題做的時候注意一下石頭是按圓形操場擺放的 不是排一排
那怎麼轉化為排成一排的呢 只需要把序列再複製一遍就可以了
轉移方程根本不用推。。
最大時 d p [ i ] [ j ] = m i n k = i j − 1 { d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + ∑ l = i j a [ l ] } dp[i][j]=min_{k=i}^{j-1}\{dp[i][k]+dp[k+1][j]+\sum_{l=i}^{j}a[l]\} dp[i][j]=mink=ij−1​{dp[i][k]+dp[k+1][j]+∑l=ij​a[l]}
最小時 d p [ i ] [ j ] = m a k = i j − 1 { d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + ∑ l = i j a [ l ] } dp[i][j]=ma_{k=i}^{j-1}\{dp[i][k]+dp[k+1][j]+\sum_{l=i}^{j}a[l]\} dp[i][j]=mak=ij−1​{dp[i][k]+dp[k+1][j]+∑l=ij​a[l]}
上程式碼:

#include<bits/stdc++.h>
using namespace std;
#define N 404
#define maxx 999999999
int n,ans,a[N],s[N],dp[N][N];
inline void read(int &x){
	int s=0,w=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}
	x=s*w;
}
int main(){
	read(n);
	for(int i=1;i<=n;i++)read(a[i]),a[i+n]=a[i];
	for(int i=1;i<=n<<1;i++)s[i]=s[i-1]+a[i];
	for(int l=1;l<n;l++){
		for(int i=1,j=l+1;j<=n<<1;i++,j++){
			dp[i][j]=maxx;
			for(int k=i;k<j;k++)dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
		}
	}
	ans=maxx;
	for(int i=1;i<=n;i++)ans=min(dp[i][i+n-1],ans);
	printf("%d\n",ans);
	for(int l=1;l<n;l++){
		for(int i=1,j=l+1;j<=n<<1;i++,j++){
			dp[i][j]=0;
			for(int k=i;k<j;k++)dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
		}
	}
	ans=0;
	for(int i=1;i<=n;i++)ans=max(dp[i][i+n-1],ans);
	printf("%d\n",ans);
}

能量項鍊

題面
$Solution:$果題 需要注意的是$i-k$區間和$k-j$區間合併時 加上的是$a[i]\times a[k+1]\times a[j+1]$ 別乘錯了！
狀態轉移方程: d p [ i ] [ j ] = m a x k = i j − 1 { d p [ i ] [ k ] + d p [ k ] [ j ] + a [ i ] × a [ k + 1 ] × a [ j + 1 ] } dp[i][j]=max_{k=i}^{j-1}\{dp[i][k]+dp[k][j]+a[i]×a[k+1]×a[j+1]\} dp[i][j]=maxk=ij−1​{dp[i][k]+dp[k][j]+a[i]×a[k+1]×a[j+1]}
程式碼↓

#include<bits/stdc++.h>
using namespace std;
#define N 220
int n,ans,a[N],dp[N][N];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		a[i+n]=a[i];
	}
	for(int l=1;l<n;l++){
		for(int i=1,j=l+1;j<=n<<1;i++,j++){
			for(int k=i;k<j;k++)dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+a[i]*a[k+1]*a[j+1]);
		}
	}
	for(int i=1;i<=n;i++)if(dp[i][i+n-1]>ans)ans=dp[i][i+n-1];
	printf("%d\n",ans);
}

凸多邊形的劃分

題目描述
給定一個具有N(N≤50)個頂點(從1到N編號)的凸多邊形，每個頂點的權均是一個正整教，
問:如何把這個凸多邊形劃分成N-2個互不相交的三角形，使得這些三角形頂點的權的乘積之和最小?

輸入
輸入檔案的第一一行為頂點數N;第二行為N個頂點(從1到N)的權值。
輸出
輸出一行為這些三角形頂點的權的乘積之和的最小值。
樣例輸入
5
121 122 123 245 231
樣例輸出
12214884
提示
$Solution:$
先將節點順時針依次編號
$dp[i][j]$表示從$i$節點到$j$節點劃分得到的乘積之和最小值
如圖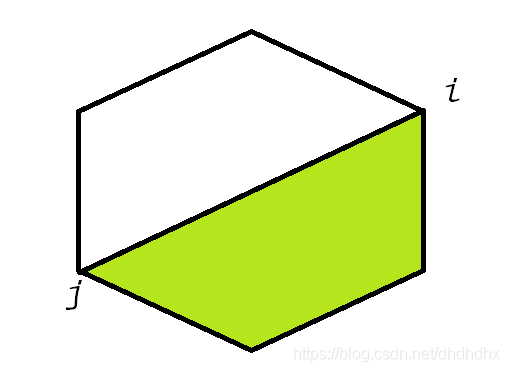
那麼如何狀態轉移呢
設$k\in (i,j)$，將$i-j$分成$i-k,k-j$來轉移

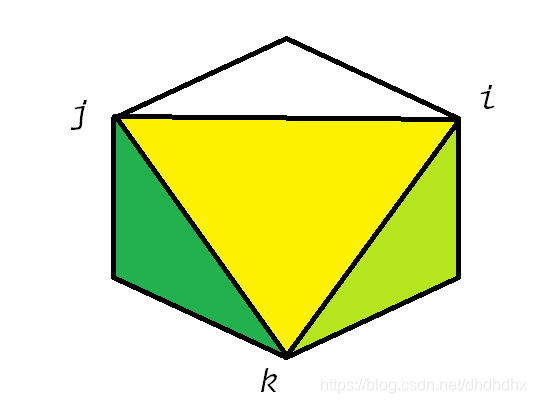
如圖，在$k$點分割之後出現了三個三角形
綠色部分分別為$dp[i][k]$和$dp[k][j]$
黃色部分為$a[i]\times a[j]\times a[k]$
那麼 d p [ i ] [ j ] = m i n k = i + 1 j − 1 { d p [ i ] [ k ] + d p [ k ] [ j ] + a [ i ] × a [ j ] × a [ k ] } dp[i][j]=min_{k=i+1}^{j-1}\{dp[i][k]+dp[k][j]+a[i]×a[j]×a[k]\} dp[i][j]=mink=i+1j−1​{dp[i][k]+dp[k][j]+a[i]×a[j]×a[k]}
初始狀態$dp[i][j]=max$，$dp[i][i+1]=0$
需要注意的是不開高精只有50分$qaq$
就當打高精模板了
上程式碼

#include<bits/stdc++.h>
using namespace std;
#define N 55
#define ll long long
ll n,a[N];
struct bigint{
	int len,s[303];
	bigint(){
		memset(s,0,sizeof(s));
		len=1;
	}
	bool operator <(const bigint &A)const{
		if(len!=A.len)return len<A.len;
		for(int i=len-1;~i;i--)
			if(s[i]!=A.s[i])return s[i]<A.s[i];
		return false;
	}
	bigint operator +(const bigint &A)const{
		bigint B;
		B.len=max(len,A.len);
		for(int i=0;i<B.len;i++){
			B.s[i]+=s[i]+A.s[i];
			B.s[i+1]+=B.s[i]/10,B.s[i]%=10;
		}
		if(B.s[B.len])B.len++;
		return B;
	}
	bigint operator *(const bigint &A)const{
		bigint B;
		B.len=len+A.len-1;
		for(int i=0;i<A.len;i++){
			for(int j=0;j<len;j++){
				B.s[i+j]+=A.s[i]*s[j];
				B.s[i+j+1]+=B.s[i+j]/10,B.s[i+j]%=10;
			}
		}
		if(B.s[B.len])B.len++;
		return B;
	}
	void print(){
		int now=len-1;
		while(!s[now]&&now)now--;
		for(int i=now;~i;i--)printf("%d",s[i]);
	}
}dp[N][N];
bigint change(ll x){
	bigint t;int cnt=0;
	while(x){
		t.s[cnt++]=x%10;
		x/=10;
	}
	t.len=cnt;
	return t;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int l=2;l<n;l++){
		for(int i=1,j=l+1;j<=n;i++,j++){
			dp[i][j].len=300,dp[i][j].s[299]=1;
			for(int k=i+1;k<j;k++){
				bigint t=change(a[i])*change(a[j])*change(a[k]);
				bigint newdp=dp[i][k]+dp[k][j]+t;
				if(newdp<dp[i][j])dp[i][j]=newdp;
			}
		}
	}
	dp[1][n].print();
}

括號配對

題面
$Solution:$判斷需要最少加幾個括號就是找最少有多少個括號沒匹配
逆向思維直接找能匹配的最多的括號
可以直接用$STL$棧過 還是練下區間$dp$吧
用$dp[i][j]$表示$i-j$區間內可以匹配到的最大括號數量
在序列$i-j$中 如果$s[i]$和$s[j]$可以匹配，則$dp[i][j]=dp[i+1][j-1]+2$
之後再直接判斷 d p [ i ] [ j ] = m a x k = i j − 1 { d p [ i ] [ k ] + d p [ k ] [ j ] } dp[i][j]=max_{k=i}^{j-1}\{dp[i][k]+dp[k][j]\} dp[i][j]=maxk=ij−1​{dp[i][k]+dp[k][j]}
上程式碼

#include<bits/stdc++.h>
using namespace std;
int n,dp[110][110];
char s[110];
int main(){
	gets(s);
	n=strlen(s);
	for(int l=1;l<n;l++){
		for(int i=0,j=l;j<n;i++,j++){
			if((s[i]=='('&&s[j]==')')||(s[i]=='['&&s[j]==']'))dp[i][j]=dp[i+1][j-1]+2;
			for(int k=i;k<j;k++)dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]);
		}
	}
	cout<<n-dp[0][n-1]<<endl;
}

分離與合體

題面
$Solution:$這題題面不太好懂，先看第一問，大概意思就是說一個序列，每兩個數可以合併成一個數，問最後合併的數最大是多少
很顯然的區間$dp$，轉移方程一眼就能看出來
d p [ i ] [ j ] = m a x k = i j − 1 { d p [ i ] [ k ] + d p [ k − 1 ] [ j ] + ( a [ i ] + a [ j ] ) × a [ k ] } dp[i][j]=max_{k=i}^{j-1}\{dp[i][k]+dp[k-1][j]+(a[i]+a[j])×a[k]\} dp[i][j]=maxk=ij−1​{dp[i][k]+dp[k−1][j]+(a[i]+a[j])×a[k]}
但是問題是第二問，如何將每次分裂記下來
設$p[i][j]$是$i$到$j$區間分裂的位置，只需在每次更新$dp[i][j]$時順便維護$p$陣列
即當$dp[i][k]+dp[k-1][j]+(a[i]+a[j])\times a[k]>dp[i][j]$時 讓$p[i][j]=k$即可
輸出時用搜尋來找每一層分裂的位置，因為除第一層外有很多個分裂點，所以用$vector$來儲存每一層分裂的位置，最後再排序輸出
需要注意的是 最後一個數不要輸出空格 不然會格式錯誤…
上程式碼

#include<bits/stdc++.h>
using namespace std;
#define N 330
int n,dep,a[N],dp[N][N],p[N][N];
vector<int> ans[N];
void dfs(int l, int r, int depth){
	if(l==r)return ;
	if(depth>dep)dep=depth;
	ans[depth].push_back(p[l][r]);
	dfs(l,p[l][r],depth+1);
	dfs(p[l][r]+1,r,depth+1);
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int l=1;l<n;l++){
		for(int i=1,j=l+1;j<=n;i++,j++){
			for(int k=i;k<j;k++){
				int now=dp[i][k]+dp[k+1][j]+(a[i]+a[j])*a[k];
				if(now>dp[i][j])dp[i][j]=now,p[i][j]=k;
			}
		}
	}
	cout<<dp[1][n]<<endl;
	dfs(1,n,1);
	for(int i=1;i<=dep;i++)sort(ans[i].begin(),ans[i].end());
	for(int i=1;i<=dep;i++){
		int siz=ans[i].size();
		for(int j=0;j<siz;j++){
			if(j==siz-1&&i==dep)printf("%d",ans[i][j]);
			else printf("%d ",ans[i][j]);
		}
	}
	cout<<endl;
}

矩陣取數遊戲

題面
$Solution:$這題還是個$NOIP$題哈哈
每行取的數只與本行之前的方案有關，所以我們只需要讓每一行都取最優
設$dp[i][j]$表示每行處理$i-j$時，當前的最優方案
則 d p [ i ] [ j ] = m a x { d p [ i − 1 ] [ j ] + 2 m − i − j + 1 , d p [ i ] [ j + 1 ] + 2 m − i − j + 1 } dp[i][j]=max\{dp[i-1][j]+2^{m-i-j+1},dp[i][j+1]+2^{m-i-j+1}\} dp[i][j]=max{dp[i−1][j]+2m−i−j+1,dp[i][j+1]+2m−i−j+1}
預處理出$2^n$，再打個高精 就可以了
程式碼在機房 不想再打一次高精了$($哭哭 週二更程式碼

總結

區間$dp$的複雜度一般都是$O(n^3)$，故資料範圍在$100$左右時可以考慮區間$dp$，區間$dp$的狀態轉移方程好想，總體來說是個不錯的解題方法。