洛谷-馬的遍歷

來源：https://www.luogu.com.cn/problem/P1443

題目描述

有一個n*m的棋盤(1<n,m<=400)，在某個點上有一個馬,要求你計算出馬到達棋盤上任意一個點最少要走幾步

輸入格式

一行四個資料，棋盤的大小和馬的座標

輸出格式

一個n*m的矩陣，代表馬到達某個點最少要走幾步（左對齊，寬5格，不能到達則輸出-1）

樣例

輸入

3 3 1 1

**輸出 **

0    3    2    
3    -1   1    
2    1    4    

看到題目第一想法是~

1：馬是怎麼走的？哈哈哈哈哈。。。

「馬」走動的方法是每步一直一斜，即先橫著或直著走一格，然後再斜著走一個對角線，俗稱「馬走日」。在「日」的對角線上兩點可以一步到達，其他地方不能到達，如圖所示。

	（x-2,y-1）		（x-2,y+1）
（x-1,y-2）				（x-1,y+2）
		(x,y)馬
（x+1,y-2）				（x+1,y+2）
	（x+2,y-1）		（x+2,y+1）

2：左對齊，寬5格咋搞，百度即得 printf("%-5d",a);

3：然後想到了廣度優先搜尋，讓我們先來解釋一下這種搜尋方式。

例如：這棵樹

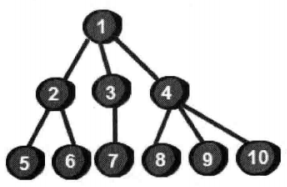
BFS搜尋，假設從1開始，然後遍歷和1相鄰的2,3,4，接著通過2,3,4遍歷5 6 7 8 9 10（注意順序）

實現過程是通過一個佇列：（這裡通過陣列表示的佇列）

1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10

當頭指標等於尾指標時，遍歷完畢，或者說符合條件的點，已經遍歷完畢。

1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10

我們可以發現每一次的遍歷都離原始點1是相同的距離，所以當我們做某些最短路徑的題時候，可以考慮一下bfs。

先來一個模板：

BFS模板（廣度優先搜尋）

void bfs()
{
	 初始化，初始狀態存陣列; 
	 int head=0,tail=1，que[max_size];//構建佇列
	 標記初始點 
	 while(head<tail)
	 {
	 	head++;//指向待擴充套件結點
		for(i=1;i<=maxi;++i)
		{
			if(滿足條件||不重複)
			{
				tail++;
				將新節點存入佇列
			}	
		}
	}
}

具體操作：

1：選擇一個二維陣列res[] [],先全部賦值為-1，裡面存放到最終結果（棋盤上每一點的最短步數）

2： 用一個結構體陣列a來表示馬所在的位置，並充當BFS模板的佇列，head,tail,充當佇列的頭尾指標

3：兩個陣列x[],y[]聯合表示馬可以到達的八個位置，用於判斷是否符合條件，然後就是要注意在判斷的時候不要越界就好啦。

然後是不是感覺來了，那就自己先試一試吧，萬一就AC了呢。

完整程式碼：

 #include<bits/stdc++.h>
int n,m,nx,ny;  
int res[405][405];//res表示最終輸出結果，下標代表棋盤位置，值代表最少步數 
int x[8]={1,2,-1,-2,-1,-2,1,2};
int y[8]={2,1,2,1,-2,-1,-2,-1};

struct queue{
	int x,y;
}a[40010];//構建bfs的佇列（用陣列表示） 

void bfs(int i,int j)
{
     int head=1,tail=2; 
     a[2].x=i,a[2].y=j;
	 res[i][j]=0;//初始位置的最少步數為0 
     while(head<tail)
	 {
        head++;
        for(int q=0;q<8;q++)
		{
			//(xx,yy)表示目前馬走到的位置，還有。。。~~變數名真的好難取~~  
            int xx=a[head].x+x[q]; 
            int yy=a[head].y+y[q];
             
            if((res[xx][yy]==-1) && xx>=1 && xx<=n && yy>=1 && yy<=m)//判斷是否走過，是否越界 
			{
                tail++;
                res[xx][yy]=res[a[head].x][a[head].y]+1;//最少步數加一 
                a[tail].x=xx;
                a[tail].y=yy;
            }
        }
    }
}

int main()
{
	
    scanf("%d%d%d%d",&n,&m,&nx,&ny);
    memset(res,-1,sizeof res);
    bfs(nx,ny);
    
    for(int i=1;i<=n;i++)
	{
        for(int j=1;j<=m;j++)
		{
			printf("%-5d",res[i][j]);
        }
        printf("\n");
    }
}

歡迎大家友好評論呀，有啥問題dd我呀。