Leetcode 二元樹的後序遍歷
0 題目描述
Leetcode原題連結:二元樹的後序遍歷
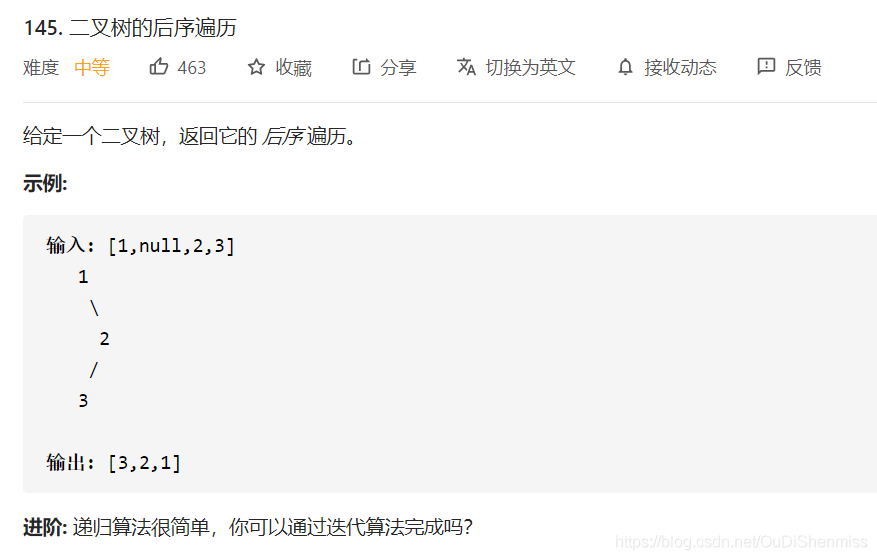
二元樹的後序遍歷:按照存取左子樹——右子樹——根節點的方式遍歷這棵樹,而在存取左子樹或者右子樹的時候,我們按照同樣的方式遍歷,直到遍歷完整棵樹。因此整個遍歷過程天然具有遞迴的性質,我們可以直接用遞迴函數來模擬這一過程。
1 遞迴解法
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
return self.postorderTraversal(root.left) + self.postorderTraversal(root.right) + [root.val]演演算法複雜度
時間複雜度:
O
(
n
)
O(n)
O(n),其中
n
n
n 為二元樹節點的個數。二元樹的遍歷中每個節點會被存取一次且只會被存取一次。
空間複雜度:
O
(
n
)
O(n)
O(n)。空間複雜度取決於遞迴的棧深度,而棧深度在二元樹為一條鏈的情況下會達到
O
(
n
)
O(n)
O(n)的級別。
2 迭代解法(堆疊)
我們也可以用迭代的方式實現方法一的遞迴函數,兩種方式是等價的,區別在於遞迴的時候隱式地維護了一個棧,而我們在迭代的時候需要顯式地將這個棧模擬出來,其餘的實現與細節都相同,具體可以參考下面的程式碼。
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
White, Gray = 0, 1
res = []
stack = [(White, root)]
while stack:
color, node = stack.pop()
if not node: continue
if color == White:
stack.append((Gray, node))
stack.append((White, node.right))
stack.append((White, node.left))
else:
res.append(node.val)
return res演演算法複雜度
時間複雜度:存取每個節點恰好一次,時間複雜度為
O
(
N
)
O(N)
O(N),其中
N
N
N是節點的個數,也就是樹的大小。
空間複雜度:取決於樹的結構,最壞情況儲存整棵樹,因此空間複雜度是
O
(
N
)
O(N)
O(N)。
3 Morris 後序遍歷
有一種巧妙的方法可以線上性時間內,只佔用常數空間來實現後序遍歷。這種方法即Morris遍歷。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def postorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
def addPath(node: TreeNode):
count = 0
while node:
count += 1
res.append(node.val)
node = node.right
i, j = len(res) - count, len(res) - 1
while i < j:
res[i], res[j] = res[j], res[i]
i += 1
j -= 1
if not root: return []
node, res = root, []
while node:
pre = node.left
if pre:
while pre.right and pre.right is not node:
pre = pre.right
if not pre.right:
pre.right = node
node = node.left
continue
else:
pre.right = None
addPath(node.left)
node = node.right
addPath(root)
return res演演算法複雜度
時間複雜度:
O
(
n
)
O(n)
O(n),其中
n
n
n是二元樹的節點數。沒有左子樹的節點只被存取一次,有左子樹的節點被存取兩次。
空間複雜度:
O
(
1
)
O(1)
O(1)。只操作已經存在的指標(樹的空閒指標),因此只需要常數的額外空間。