確定部分分式中待定係數的留數方法
確定部分分式中待定係數的留數方法
在將有理真分式化為確定部分分式和的過程中,可以使用留數對部分分式的係數進行求解。
這裡介紹一篇論文,證明可以在論文中檢視
設有理真分式
f
(
x
)
=
P
m
(
x
)
Q
n
(
x
)
f(x)=\frac{P_m(x)}{Q_n(x)}
f(x)=Qn(x)Pm(x)
其中,
m
≤
n
m\le n
m≤n
分為以下兩種 情況進行討論
a. Q(x)=0的根均為單根
 .
.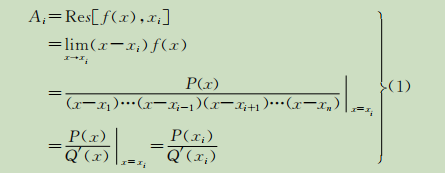
即,此時要確定的係數就是f(x)在對應極點上的留數
b.根中有重根

單根的確定方法同a情況中的確定方法,對於重根,設x1 為r重根,考慮Bk
B
k
=
R
e
s
[
(
x
−
x
1
)
k
−
1
f
(
x
)
,
x
1
]
此
時
x
1
為
(
x
−
x
1
)
k
−
1
f
(
x
)
的
r
−
(
k
−
1
)
=
r
−
k
+
1
級
極
點
B_k=Res[(x-x_1)^{k-1}f(x),x_1 ] \\ 此時x_1為(x-x_1)^{k-1}f(x)的r-(k-1)=r-k+1級極點
Bk=Res[(x−x1)k−1f(x),x1]此時x1為(x−x1)k−1f(x)的r−(k−1)=r−k+1級極點
利用留數極點計算公式 得,
B
k
=
1
(
r
−
k
)
!
lim
x
→
x
1
[
(
x
−
x
1
)
r
f
(
x
)
]
r
−
k
=
1
(
r
−
k
)
!
[
(
x
−
x
1
)
r
f
(
x
)
]
r
−
k
∣
x
=
x
1
B_k=\frac{1}{(r-k)!}\lim_{x \to x_1} [(x-x_1)^{r}f(x)]^{r-k} \\{\color{Blue}=\frac{1}{(r-k)!}[(x-x_1)^rf(x)]^{r-k}|_{x=x_1} }
Bk=(r−k)!1x→x1lim[(x−x1)rf(x)]r−k=(r−k)!1[(x−x1)rf(x)]r−k∣x=x1
注:上述結論雖然是在實根條件下得出的,但經過博主研究,上述結論在根為複數單根,以及複數重根的條件下同樣成立。
c.總結——基本思想
要 將 有 理 真 分 式 f ( x ) = P m ( x ) Q n ( x ) 在 實 數 範 圍 內 化 為 部 分 分 式 和 的 形 式 , 可 將 f ( x ) 視 為 特 殊 的 復 變 函 數 f ( z ) 先 將 f ( z ) 化 為 部 分 分 式 和 的 形 式 , 根 據 復 變 函 數 的 積 分 和 留 數 理 論 可 得 其 待 定 系 數 為 f ( z ) 在 極 點 處 的 留 數 要將有理真分式\\ f(x)=\frac{P_m(x)}{Q_n(x)} \\在實數範圍內化為部分分式和的形式,可將f(x)視為特殊的複變函數f(z) \\先將f(z)化為部分分式和的形式,根據複變函數的積分和留數理論可得 \\其待定係數為f(z)在極點處的留數 要將有理真分式f(x)=Qn(x)Pm(x)在實數範圍內化為部分分式和的形式,可將f(x)視為特殊的復變函數f(z)先將f(z)化為部分分式和的形式,根據復變函數的積分和留數理論可得其待定系數為f(z)在極點處的留數