機器學習——【2】特徵工程
2.1 資料集
2.1.1 可用資料集
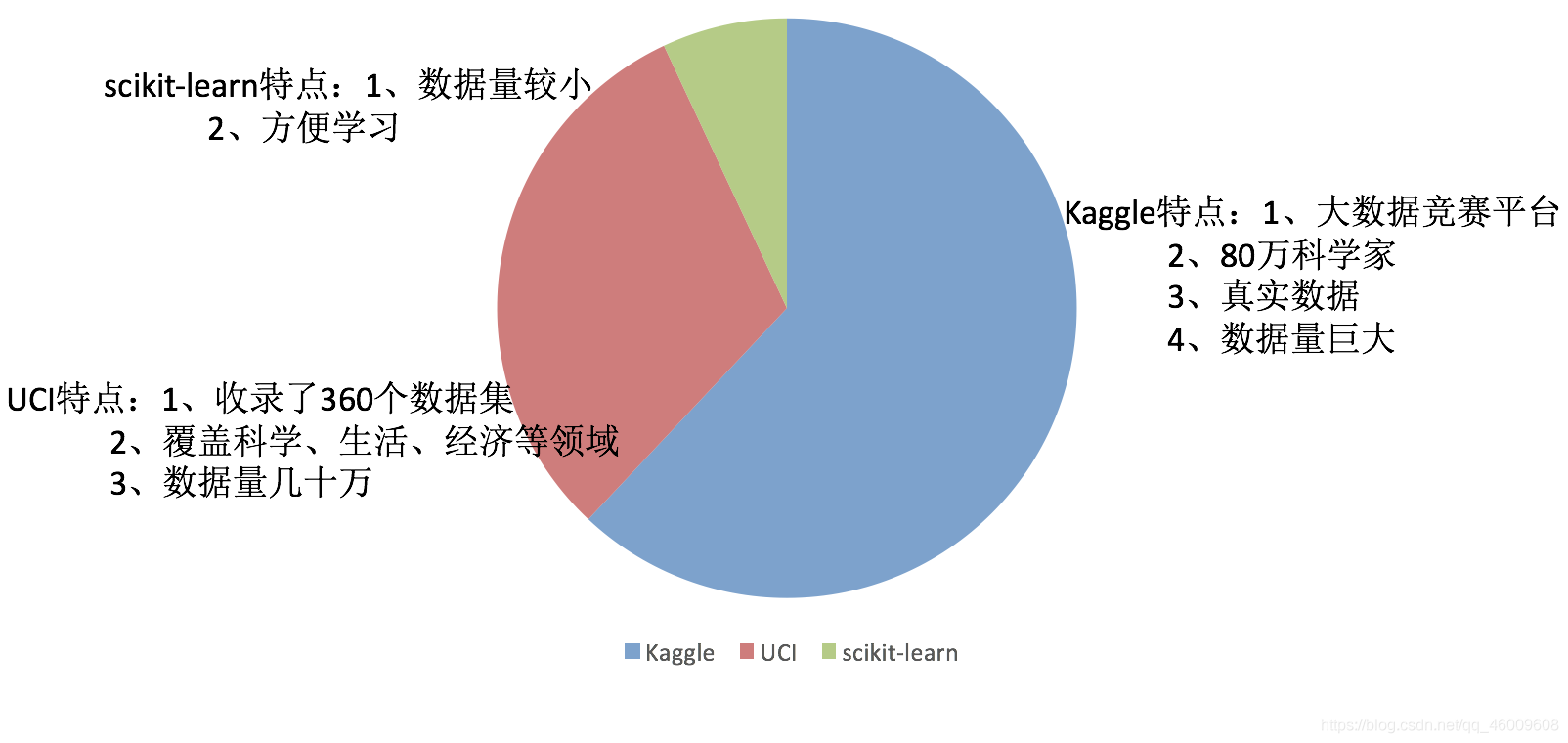
Kaggle網址:https://www.kaggle.com/datasets
UCI資料集網址: http://archive.ics.uci.edu/ml/
scikit-learn網址:http://scikit-learn.org/stable/datasets/index.html#datasets
(1)Scikit-learn工具介紹

Python語言的機器學習工具
Scikit-learn包括許多知名的機器學習演演算法的實現
Scikit-learn檔案完善,容易上手,豐富的API
目前穩定版本0.19.1
(2)Scikit-learn包含的內容:
- 分類、聚類、迴歸
- 特徵工程
- 模型選擇、調優
2.1.2 sklearn資料集
(1)scikit-learn資料集API介紹
sklearn.datasets
載入獲取流行資料集
datasets.load_()
獲取小規模資料集,資料包含在datasets裡
datasets.fetch_(data_home=None)
獲取大規模資料集,需要從網路上下載,函數的第一個引數是data_home,表示資料集下載的目錄,預設是 ~/scikit_learn_data/
(2)sklearn小資料集
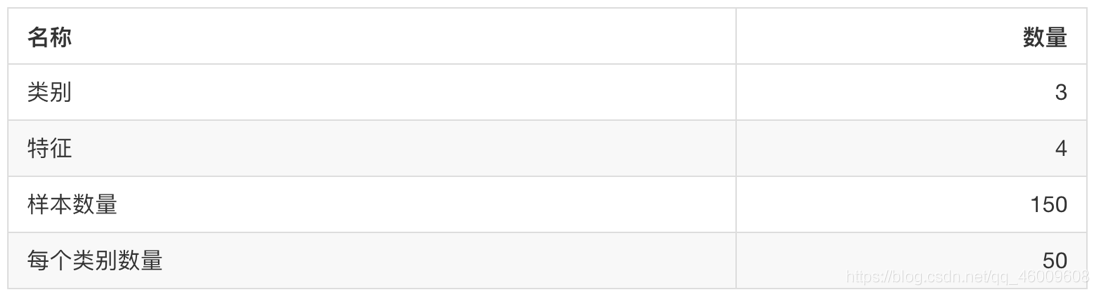
sklearn.datasets.load_iris()
載入並返回鳶尾花資料集
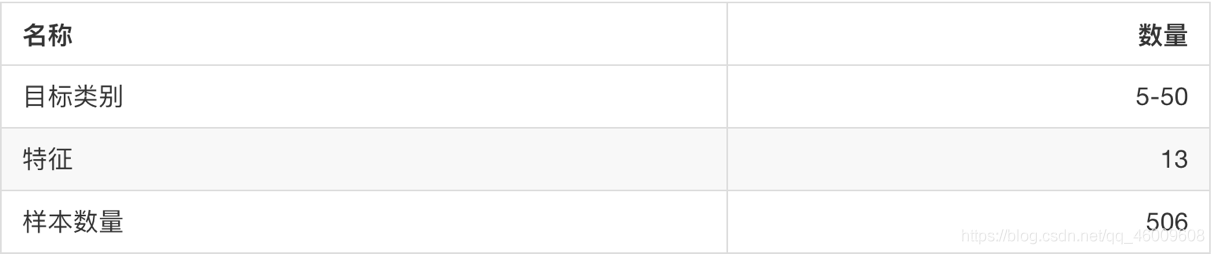
sklearn.datasets.load_boston()
載入並返回波士頓房價資料集
(3)sklearn巨量資料集
sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
subset:‘train’或者’test’,‘all’,可選,選擇要載入的資料集。
訓練集的「訓練」,測試集的「測試」,兩者的「全部」
(4)sklearn資料集的使用
以鳶尾花資料集為例:

sklearn資料集返回值介紹
load和fetch返回的資料型別datasets.base.Bunch(字典格式)
data:特徵資料陣列,是 [n_samples * n_features] 的二維 numpy.ndarray 陣列
target:標籤陣列,是 n_samples 的一維 numpy.ndarray 陣列
DESCR:資料描述
feature_names:特徵名,新聞資料,手寫數位、迴歸資料集沒有
target_names:標籤名
from sklearn.datasets import load_iris
# 獲取鳶尾花資料集
iris = load_iris()
print("鳶尾花資料集的返回值:\n", iris)
# 返回值是一個繼承自字典的Bench
print("鳶尾花的特徵值:\n", iris["data"])
print("鳶尾花的目標值:\n", iris.target)
print("鳶尾花特徵的名字:\n", iris.feature_names)
print("鳶尾花目標值的名字:\n", iris.target_names)
print("鳶尾花的描述:\n", iris.DESCR)
思考:拿到的資料是否全部都用來訓練一個模型?
2.1.3 資料集的劃分
機器學習一般的資料集會劃分為兩個部分:
訓練資料:用於訓練,構建模型
測試資料:在模型檢驗時使用,用於評估模型是否有效
劃分比例:
訓練集:70% 80% 75%
測試集:30% 20% 30%
資料集劃分api
sklearn.model_selection.train_test_split(arrays, *options)
x 資料集的特徵值
y 資料集的標籤值
test_size 測試集的大小,一般為float
random_state 亂數種子,不同的種子會造成不同的隨機取樣結果。相同的種子取樣結果相同。
return 測試集特徵訓練集特徵值值,訓練標籤,測試標籤(預設隨機取)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def datasets_demo():
"""
對鳶尾花資料集的演示
:return: None
"""
# 1、獲取鳶尾花資料集
iris = load_iris()
print("鳶尾花資料集的返回值:\n", iris)
# 返回值是一個繼承自字典的Bench
print("鳶尾花的特徵值:\n", iris["data"])
print("鳶尾花的目標值:\n", iris.target)
print("鳶尾花特徵的名字:\n", iris.feature_names)
print("鳶尾花目標值的名字:\n", iris.target_names)
print("鳶尾花的描述:\n", iris.DESCR)
# 2、對鳶尾花資料集進行分割
# 訓練集的特徵值x_train 測試集的特徵值x_test 訓練集的目標值y_train 測試集的目標值y_test
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
print("x_train:\n", x_train.shape)
# 亂數種子
x_train1, x_test1, y_train1, y_test1 = train_test_split(iris.data, iris.target, random_state=6)
x_train2, x_test2, y_train2, y_test2 = train_test_split(iris.data, iris.target, random_state=6)
print("如果亂數種子不一致:\n", x_train == x_train1)
print("如果亂數種子一致:\n", x_train1 == x_train2)
return None
2.2 特徵工程介紹
2.2.1 為什麼需要特徵工程(Feature Engineering)
機器學習領域的大神Andrew Ng(吳恩達)老師說「Coming up with features is difficult, time-consuming, requires expert knowledge. 「Applied machine learning」 is basically feature engineering. 」
注:業界廣泛流傳:資料和特徵決定了機器學習的上限,而模型和演演算法只是逼近這個上限而已。
2.2.2 什麼是特徵工程
特徵工程是使用專業背景知識和技巧處理資料,使得特徵能在機器學習演演算法上發揮更好的作用的過程。
意義:會直接影響機器學習的效果。
2.2.3 特徵工程的位置與資料處理的比較

pandas:一個資料讀取非常方便以及基本的處理格式的工具;
sklearn:對於特徵的處理提供了強大的介面;
特徵工程包含內容
特徵抽取;
特徵預處理;
特徵降維;
2.3 特徵提取
2.3.1 特徵提取
(1) 將任意資料(如文字或影象)轉換為可用於機器學習的數位特徵
注:特徵值化是為了計算機更好的去理解資料
- 字典特徵提取(特徵離散化)
- 文字特徵提取
- 影象特徵提取(深度學習中會介紹)
(2) 特徵提取API
sklearn.feature_extraction
2.3.2 字典特徵提取
作用:對字典資料進行特徵值化
sklearn.feature_extraction.DictVectorizer(sparse=True,…)
DictVectorizer.fit_transform(X) X:字典或者包含字典的迭代器返回值:返回sparse矩陣
DictVectorizer.inverse_transform(X) X:array陣列或者sparse矩陣 返回值:轉換之前資料格式
DictVectorizer.get_feature_names() 返回類別名稱
(1)應用
我們對以下資料進行特徵提取
[{'city': '北京','temperature':100}
{'city': '上海','temperature':60}
{'city': '深圳','temperature':30}]

(2)流程分析
範例化類DictVectorizer
呼叫fit_transform方法輸入資料並轉換(注意返回格式)
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
"""
對字典型別的資料進行特徵抽取
:return: None
"""
data = [{'city': '北京','temperature':100}, {'city': '上海','temperature':60}, {'city': '深圳','temperature':30}]
# 1、範例化一個轉換器類
transfer = DictVectorizer(sparse=False)
# 2、呼叫fit_transform
data = transfer.fit_transform(data)
print("返回的結果:\n", data)
# 列印特徵名字
print("特徵名字:\n", transfer.get_feature_names())
return None
注意觀察沒有加上sparse=False引數的結果
返回的結果:
(0, 1) 1.0
(0, 3) 100.0
(1, 0) 1.0
(1, 3) 60.0
(2, 2) 1.0
(2, 3) 30.0
特徵名字:
['city=上海', 'city=北京', 'city=深圳', 'temperature']
這個結果並不是我們想要看到的,所以加上引數,得到想要的結果:
返回的結果:
[[ 0. 1. 0. 100.]
[ 1. 0. 0. 60.]
[ 0. 0. 1. 30.]]
特徵名字:
['city=上海', 'city=北京', 'city=深圳', 'temperature']
之前在學習pandas中的離散化的時候,也實現了類似的效果。
我們把這個處理資料的技巧叫做」one-hot「編碼:
轉化為:
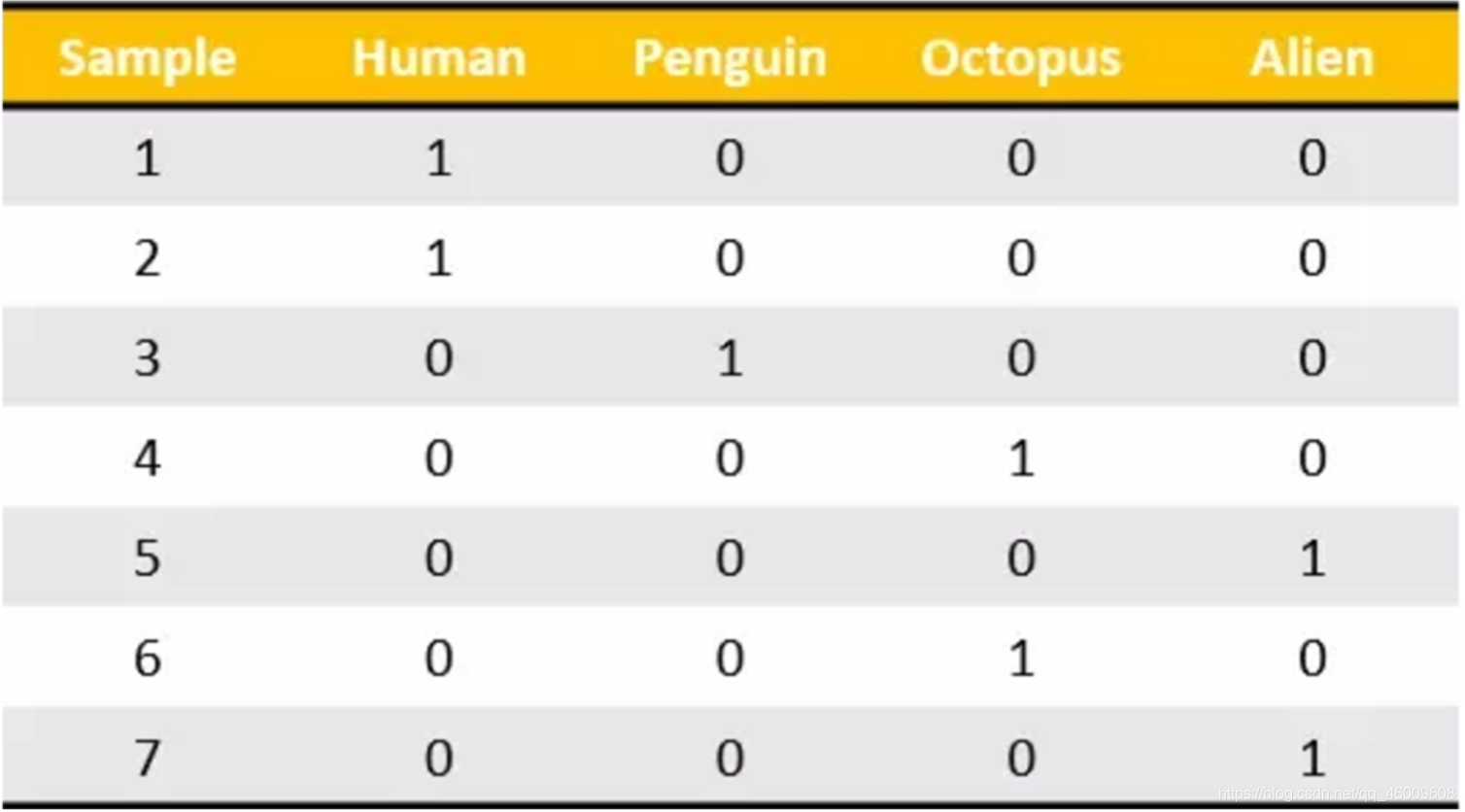
** 總結**
對於特徵當中存在類別資訊的我們都會做one-hot編碼處理
2.3.3 文字特徵提取
作用:對文字資料進行特徵值化
sklearn.feature_extraction.text.CountVectorizer(stop_words=[])
返回詞頻矩陣
CountVectorizer.fit_transform(X) X:文字或者包含文字字串的可迭代物件 返回值:返回sparse矩陣
CountVectorizer.inverse_transform(X) X:array陣列或者sparse矩陣 返回值:轉換之前資料格
CountVectorizer.get_feature_names() 返回值:單詞列表
sklearn.feature_extraction.text.TfidfVectorizer
(1)應用
我們對以下資料進行特徵提取
["life is short,i like python",
"life is too long,i dislike python"]

(2)流程分析
範例化類CountVectorizer
呼叫fit_transform方法輸入資料並轉換 (注意返回格式,利用toarray()進行sparse矩陣轉換array陣列)
from sklearn.feature_extraction.text import CountVectorizer
def text_count_demo():
"""
對文字進行特徵抽取,countvetorizer
:return: None
"""
data = ["life is short,i like like python", "life is too long,i dislike python"]
# 1、範例化一個轉換器類
# transfer = CountVectorizer(sparse=False)
transfer = CountVectorizer()
# 2、呼叫fit_transform
data = transfer.fit_transform(data)
print("文字特徵抽取的結果:\n", data.toarray())
print("返回特徵名字:\n", transfer.get_feature_names())
return None
返回結果:
文字特徵抽取的結果:
[[0 1 1 2 0 1 1 0]
[1 1 1 0 1 1 0 1]]
返回特徵名字:
['dislike', 'is', 'life', 'like', 'long', 'python', 'short', 'too']
問題:如果我們將資料替換成中文?
"人生苦短,我喜歡Python" "生活太長久,我不喜歡Python"
那麼最終得到的結果是:
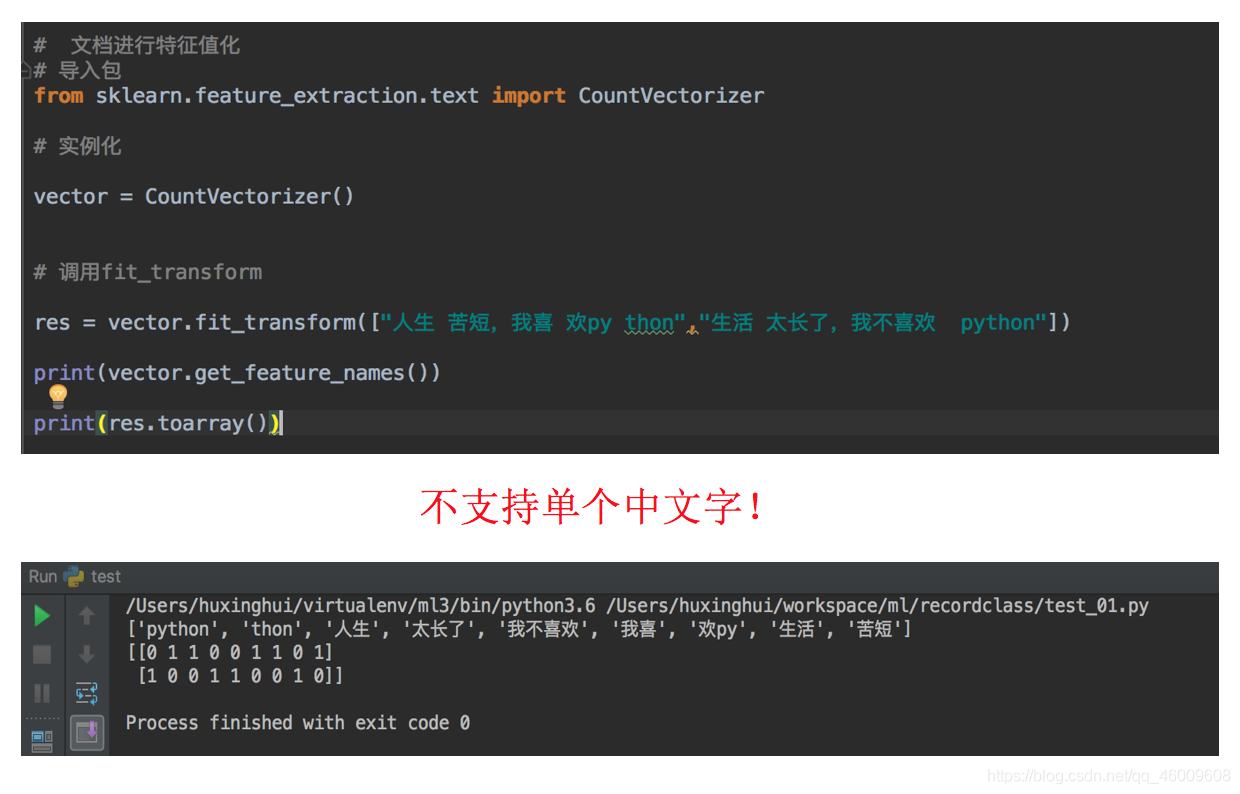
為什麼會得到這樣的結果呢,仔細分析之後會發現英文預設是以空格分開的。其實就達到了一個分詞的效果,所以我們要對中文進行分詞處理。
(3)jieba分詞處理
jieba.cut()
返回詞語組成的生成器
需要安裝下jieba庫
pip3 install jieba
(4)案例分析
對以下三句話進行特徵值化
今天很殘酷,明天更殘酷,後天很美好,
但絕對大部分是死在明天晚上,所以每個人不要放棄今天。
我們看到的從很遠星系來的光是在幾百萬年之前發出的,
這樣當我們看到宇宙時,我們是在看它的過去。
如果只用一種方式瞭解某樣事物,你就不會真正瞭解它。
瞭解事物真正含義的祕密取決於如何將其與我們所瞭解的事物相聯絡。
分析
準備句子,利用jieba.cut進行分詞
範例化CountVectorizer
將分詞結果變成字串當作fit_transform的輸入值

from sklearn.feature_extraction.text import CountVectorizer
import jieba
def cut_word(text):
"""
對中文進行分詞
"我愛北京天安門"————>"我 愛 北京 天安門"
:param text:
:return: text
"""
# 用結巴對中文字串進行分詞
text = " ".join(list(jieba.cut(text)))
return text
def text_chinese_count_demo2():
"""
對中文進行特徵抽取
:return: None
"""
data = ["一種還是一種今天很殘酷,明天更殘酷,後天很美好,但絕對大部分是死在明天晚上,所以每個人不要放棄今天。",
"我們看到的從很遠星系來的光是在幾百萬年之前發出的,這樣當我們看到宇宙時,我們是在看它的過去。",
"如果只用一種方式瞭解某樣事物,你就不會真正瞭解它。瞭解事物真正含義的祕密取決於如何將其與我們所瞭解的事物相聯絡。"]
# 將原始資料轉換成分好詞的形式
text_list = []
for sent in data:
text_list.append(cut_word(sent))
print(text_list)
# 1、範例化一個轉換器類
# transfer = CountVectorizer(sparse=False)
transfer = CountVectorizer()
# 2、呼叫fit_transform
data = transfer.fit_transform(text_list)
print("文字特徵抽取的結果:\n", data.toarray())
print("返回特徵名字:\n", transfer.get_feature_names())
return None
返回結果:
Building prefix dict from the default dictionary ...
Dumping model to file cache /var/folders/mz/tzf2l3sx4rgg6qpglfb035_r0000gn/T/jieba.cache
Loading model cost 1.032 seconds.
['一種 還是 一種 今天 很 殘酷 , 明天 更 殘酷 , 後天 很 美好 , 但 絕對 大部分 是 死 在 明天 晚上 , 所以 每個 人 不要 放棄 今天 。', '我們 看到 的 從 很 遠 星系 來 的 光是在 幾百萬年 之前 發出 的 , 這樣 當 我們 看到 宇宙 時 , 我們 是 在 看 它 的 過去 。', '如果 只用 一種 方式 瞭解 某樣 事物 , 你 就 不會 真正 瞭解 它 。 瞭解 事物 真正 含義 的 祕密 取決於 如何 將 其 與 我們 所 瞭解 的 事物 相 聯絡 。']
Prefix dict has been built succesfully.
文字特徵抽取的結果:
[[2 0 1 0 0 0 2 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 2 0 1 0 2 1 0 0 0 1 1 0 0 1 0]
[0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 3 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 1 0 1]
[1 1 0 0 4 3 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0 1 0 0 0 1 0 0 0 2 1 0 0 1 0 0 0]]
返回特徵名字:
['一種', '不會', '不要', '之前', '瞭解', '事物', '今天', '光是在', '幾百萬年', '發出', '取決於', '只用', '後天', '含義', '大部分', '如何', '如果', '宇宙', '我們', '所以', '放棄', '方式', '明天', '星系', '晚上', '某樣', '殘酷', '每個', '看到', '真正', '祕密', '絕對', '美好', '聯絡', '過去', '還是', '這樣']
但如果把這樣的詞語特徵用於分類,會出現什麼問題?
請看問題:
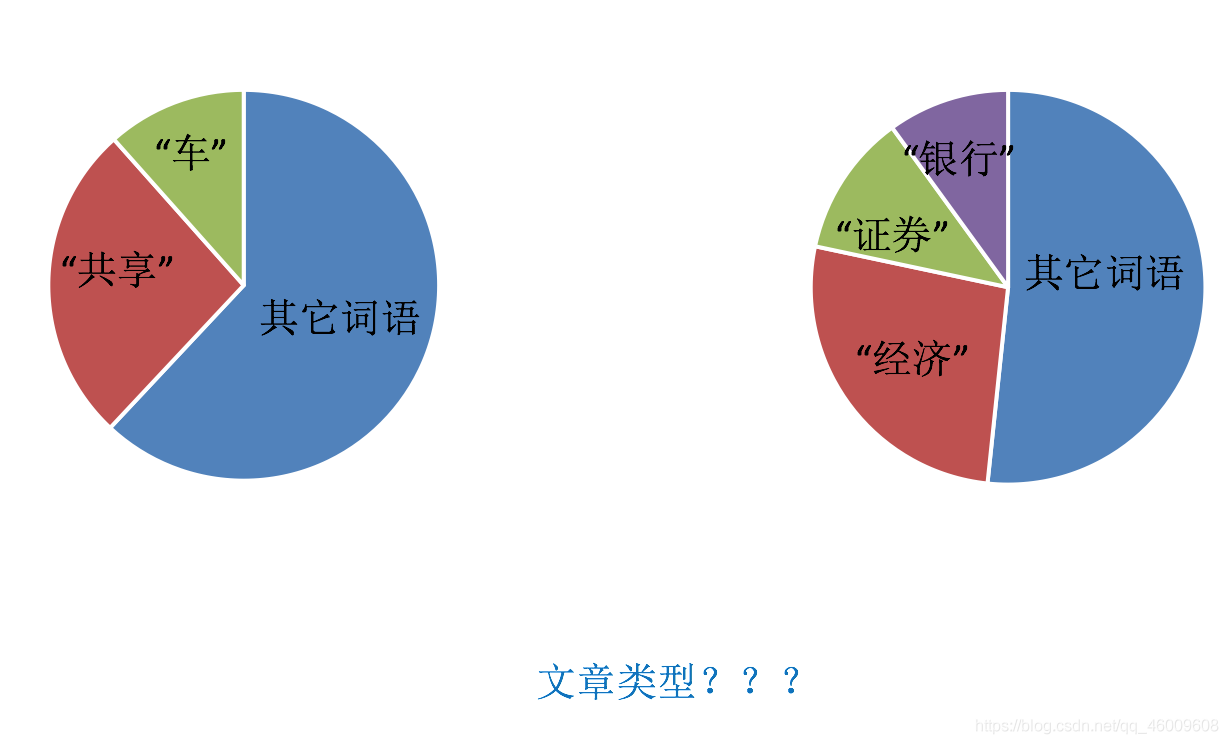
該如何處理某個詞或短語在多篇文章中出現的次數高這種情況?
(5)Tf-idf文字特徵提取
TF-IDF的主要思想是:如果某個詞或短語在一篇文章中出現的概率高,並且在其他文章中很少出現,則認為此詞或者短語具有很好的類別區分能力,適合用來分類。
TF-IDF作用:用以評估一字詞對於一個檔案集或一個語料庫中的其中一份檔案的重要程度。
(5.1)公式
詞頻(term frequency,tf)指的是某一個給定的詞語在該檔案中出現的頻率
逆向檔案頻率(inverse document frequency,idf)是一個詞語普遍重要性的度量。某一特定詞語的idf,可以由總檔案數目除以包含該詞語之檔案的數目,再將得到的商取以10為底的對數得到
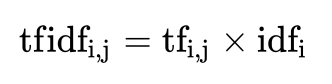
最終得出結果可以理解為重要程度。
注:假如一篇檔案的總詞語數是100個,而詞語"非常"出現了5次,那麼"非常"一詞在該檔案中的詞頻就是5/100=0.05。而計算檔案頻率(IDF)的方法是以檔案集的檔案總數,除以出現"非常"一詞的檔案數。所以,如果"非常"一詞在1,000份檔案出現過,而檔案總數是10,000,000份的話,其逆向檔案頻率就是lg(10,000,000 / 1,0000)=3。最後"非常"對於這篇檔案的tf-idf的分數為0.05 * 3=0.15
(5.2 )案例
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def cut_word(text):
"""
對中文進行分詞
"我愛北京天安門"————>"我 愛 北京 天安門"
:param text:
:return: text
"""
# 用結巴對中文字串進行分詞
text = " ".join(list(jieba.cut(text)))
return text
def text_chinese_tfidf_demo():
"""
對中文進行特徵抽取
:return: None
"""
data = ["一種還是一種今天很殘酷,明天更殘酷,後天很美好,但絕對大部分是死在明天晚上,所以每個人不要放棄今天。",
"我們看到的從很遠星系來的光是在幾百萬年之前發出的,這樣當我們看到宇宙時,我們是在看它的過去。",
"如果只用一種方式瞭解某樣事物,你就不會真正瞭解它。瞭解事物真正含義的祕密取決於如何將其與我們所瞭解的事物相聯絡。"]
# 將原始資料轉換成分好詞的形式
text_list = []
for sent in data:
text_list.append(cut_word(sent))
print(text_list)
# 1、範例化一個轉換器類
# transfer = CountVectorizer(sparse=False)
transfer = TfidfVectorizer(stop_words=['一種', '不會', '不要'])
# 2、呼叫fit_transform
data = transfer.fit_transform(text_list)
print("文字特徵抽取的結果:\n", data.toarray())
print("返回特徵名字:\n", transfer.get_feature_names())
return None
返回結果:
Building prefix dict from the default dictionary ...
Loading model from cache /var/folders/mz/tzf2l3sx4rgg6qpglfb035_r0000gn/T/jieba.cache
Loading model cost 0.856 seconds.
Prefix dict has been built succesfully.
['一種 還是 一種 今天 很 殘酷 , 明天 更 殘酷 , 後天 很 美好 , 但 絕對 大部分 是 死 在 明天 晚上 , 所以 每個 人 不要 放棄 今天 。', '我們 看到 的 從 很 遠 星系 來 的 光是在 幾百萬年 之前 發出 的 , 這樣 當 我們 看到 宇宙 時 , 我們 是 在 看 它 的 過去 。', '如果 只用 一種 方式 瞭解 某樣 事物 , 你 就 不會 真正 瞭解 它 。 瞭解 事物 真正 含義 的 祕密 取決於 如何 將 其 與 我們 所 瞭解 的 事物 相 聯絡 。']
文字特徵抽取的結果:
[[ 0. 0. 0. 0.43643578 0. 0. 0.
0. 0. 0.21821789 0. 0.21821789 0. 0.
0. 0. 0.21821789 0.21821789 0. 0.43643578
0. 0.21821789 0. 0.43643578 0.21821789 0. 0.
0. 0.21821789 0.21821789 0. 0. 0.21821789
0. ]
[ 0.2410822 0. 0. 0. 0.2410822 0.2410822
0.2410822 0. 0. 0. 0. 0. 0.
0. 0.2410822 0.55004769 0. 0. 0. 0.
0.2410822 0. 0. 0. 0. 0.48216441
0. 0. 0. 0. 0. 0.2410822
0. 0.2410822 ]
[ 0. 0.644003 0.48300225 0. 0. 0. 0.
0.16100075 0.16100075 0. 0.16100075 0. 0.16100075
0.16100075 0. 0.12244522 0. 0. 0.16100075
0. 0. 0. 0.16100075 0. 0. 0.
0.3220015 0.16100075 0. 0. 0.16100075 0. 0.
0. ]]
返回特徵名字:
['之前', '瞭解', '事物', '今天', '光是在', '幾百萬年', '發出', '取決於', '只用', '後天', '含義', '大部分', '如何', '如果', '宇宙', '我們', '所以', '放棄', '方式', '明天', '星系', '晚上', '某樣', '殘酷', '每個', '看到', '真正', '祕密', '絕對', '美好', '聯絡', '過去', '還是', '這樣']
(6)Tf-idf的重要性
分類機器學習演演算法進行文章分類中前期資料處理方式
2.4 特徵預處理
2.4.1 什麼是特徵預處理
# scikit-learn的解釋
provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.
翻譯過來:通過一些轉換函數將特徵資料轉換成更加適合演演算法模型的特徵資料過程
可以通過下面那張圖來理解
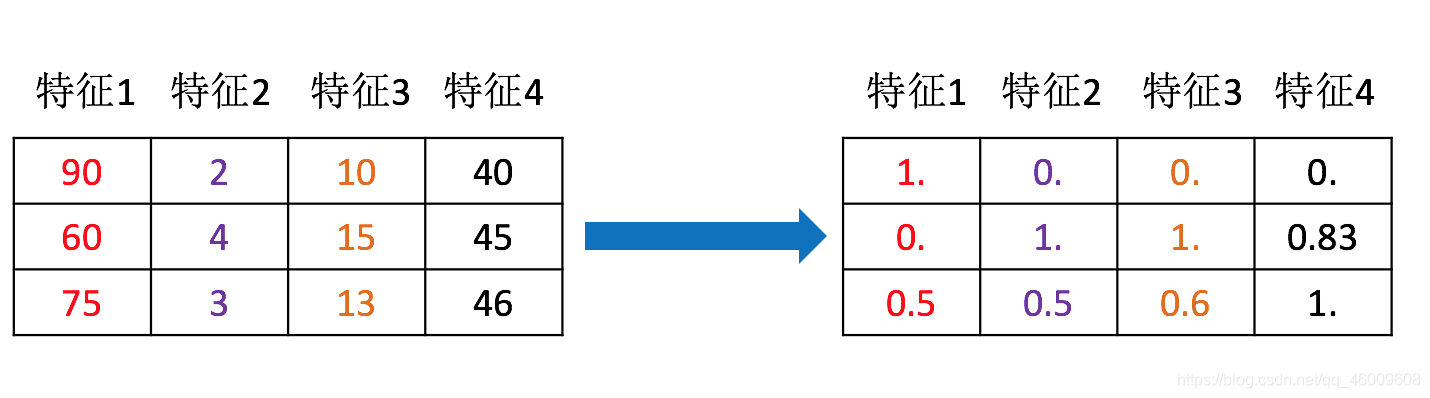
(1)包含內容
數值型資料的無量綱化:
歸一化
標準化
(2)特徵預處理API
sklearn.preprocessing
為什麼我們要進行歸一化/標準化?
特徵的單位或者大小相差較大,或者某特徵的方差相比其他的特徵要大出幾個數量級,容易影響(支配)目標結果,使得一些演演算法無法學習到其它的特徵.
約會物件資料:
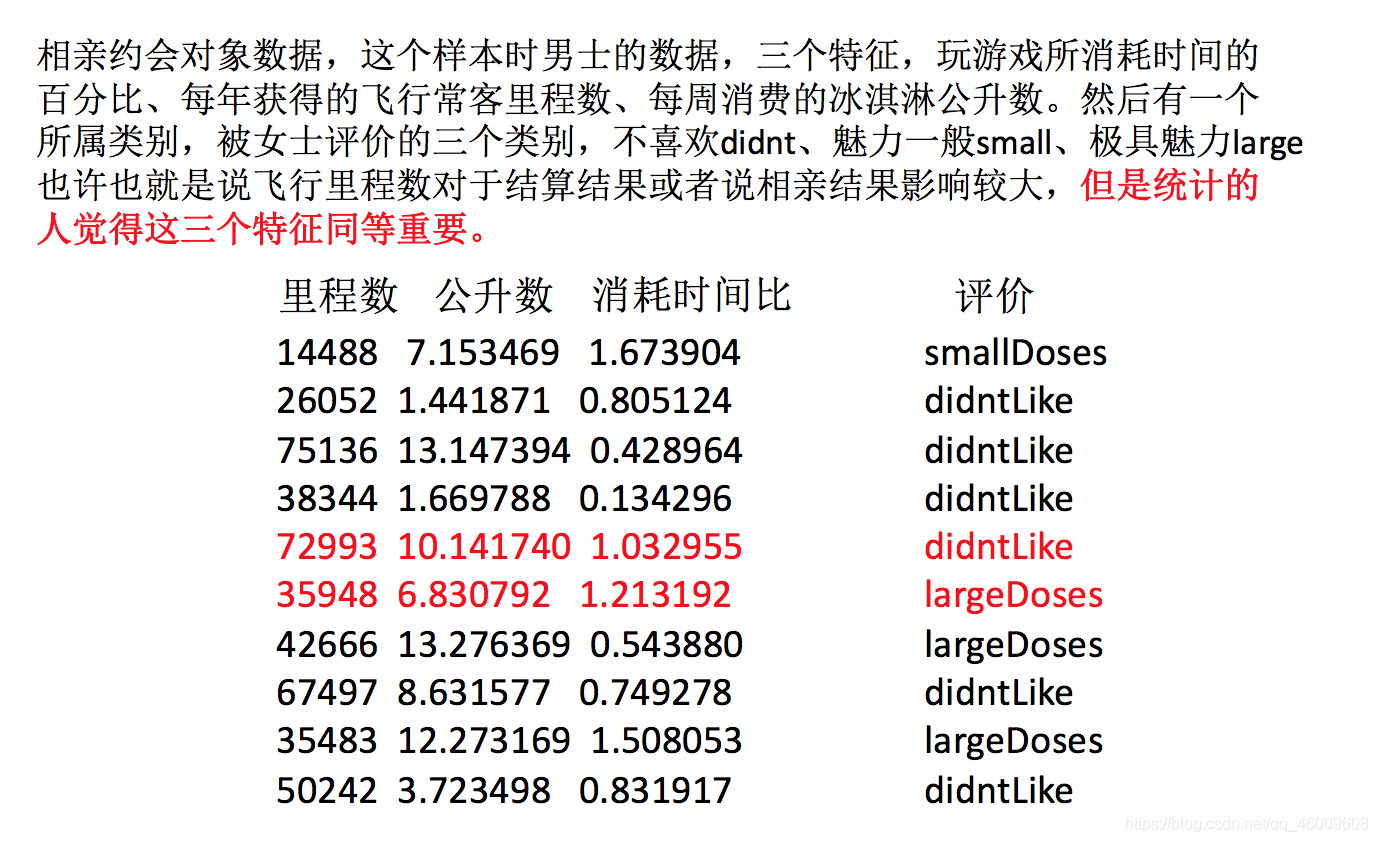
我們需要用到一些方法進行無量綱化,使不同規格的資料轉換到同一規格
2.4.2 歸一化
(1)定義
通過對原始資料進行變換把資料對映到(預設為[0,1])之間
(2)公式
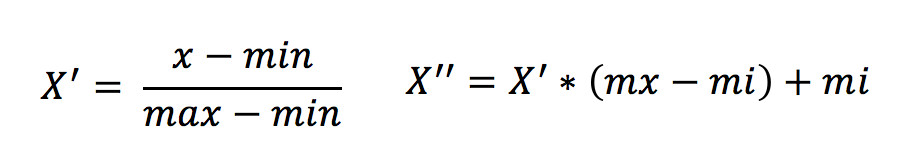
作用於每一列,max為一列的最大值,min為一列的最小值,那麼X’’為最終結果,mx,mi分別為指定區間值預設mx為1,mi為0
那麼怎麼理解這個過程呢?我們通過一個例子
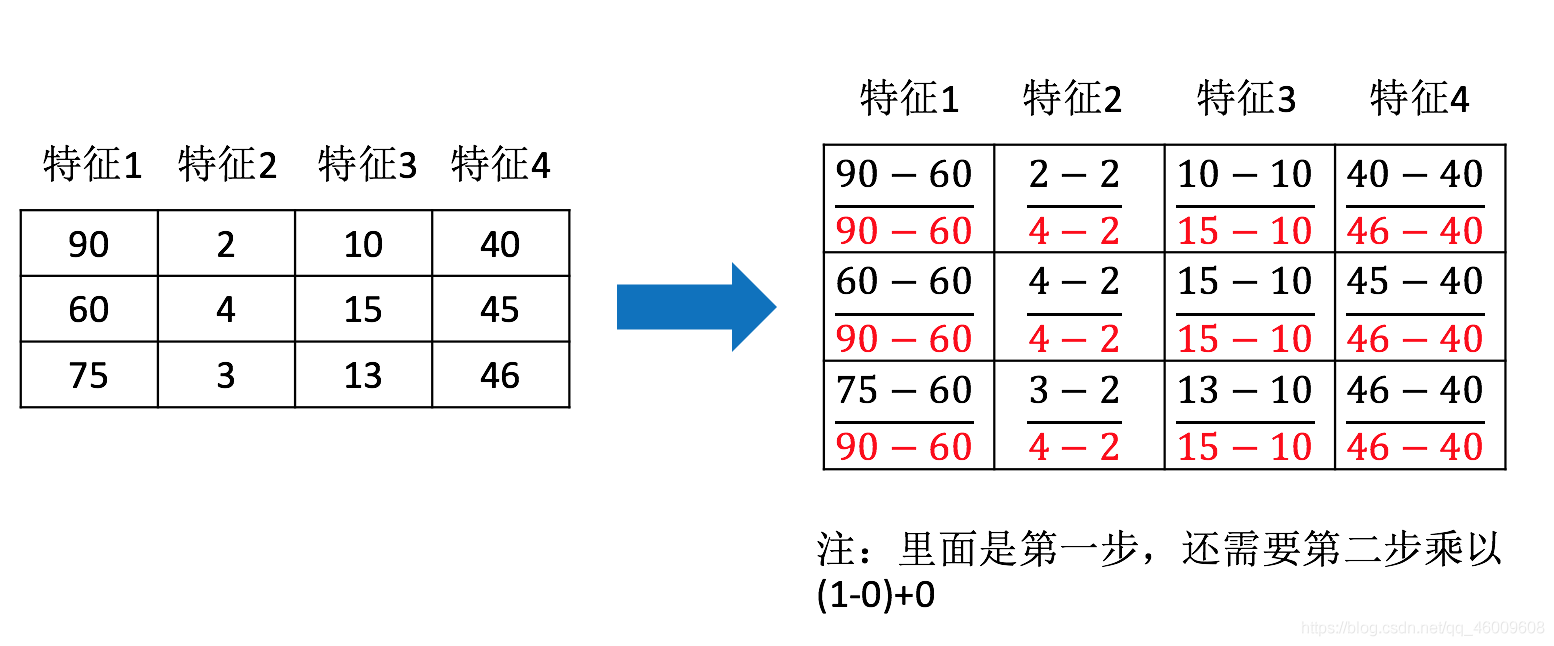
(3)API
sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
MinMaxScalar.fit_transform(X)
X:numpy array格式的資料[n_samples,n_features]
返回值:轉換後的形狀相同的array
(4)資料計算
我們對以下資料進行運算,在dating.txt中。儲存的就是之前的約會物件資料。
milage,Liters,Consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1
38344,1.669788,0.134296,1
分析
1、範例化MinMaxScalar
2、通過fit_transform轉換
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
def minmax_demo():
"""
歸一化演示
:return: None
"""
data = pd.read_csv("dating.txt")
print(data)
# 1、範例化一個轉換器類
transfer = MinMaxScaler(feature_range=(2, 3))
# 2、呼叫fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("最小值最大值歸一化處理的結果:\n", data)
return None
返回結果:
milage Liters Consumtime target
0 40920 8.326976 0.953952 3
1 14488 7.153469 1.673904 2
2 26052 1.441871 0.805124 1
3 75136 13.147394 0.428964 1
.. ... ... ... ...
998 48111 9.134528 0.728045 3
999 43757 7.882601 1.332446 3
[1000 rows x 4 columns]
最小值最大值歸一化處理的結果:
[[ 2.44832535 2.39805139 2.56233353]
[ 2.15873259 2.34195467 2.98724416]
[ 2.28542943 2.06892523 2.47449629]
...,
[ 2.29115949 2.50910294 2.51079493]
[ 2.52711097 2.43665451 2.4290048 ]
[ 2.47940793 2.3768091 2.78571804]]
問題:如果資料中異常點較多,會有什麼影響?
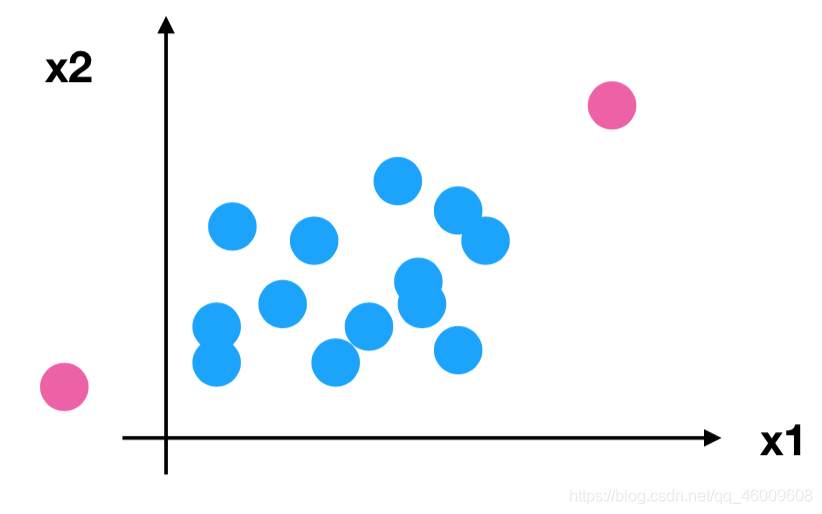
(5)歸一化總結
注意最大值最小值是變化的,另外,最大值與最小值非常容易受異常點影響,所以這種方法魯棒性較差,只適合傳統精確小資料場景。
怎麼辦?
2.4.3 標準化
(1)定義
通過對原始資料進行變換把資料變換到均值為0,標準差為1範圍內
(2) 公式
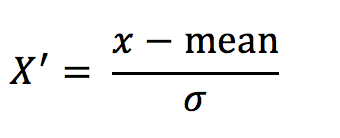
作用於每一列,mean為平均值,σ為標準差
所以回到剛才異常點的地方,我們再來看看標準化
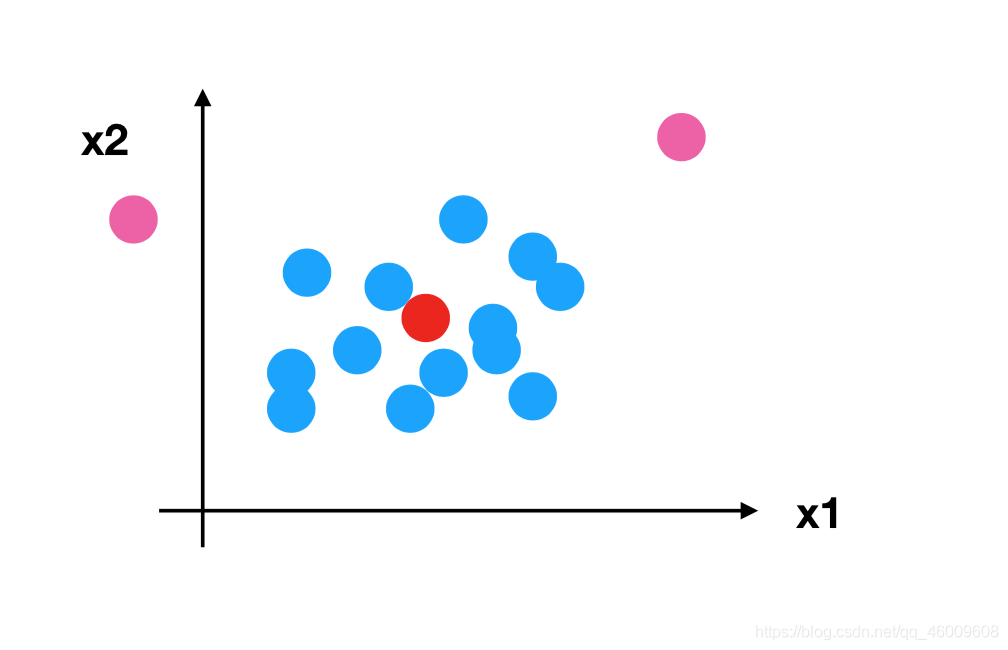
對於歸一化來說:如果出現異常點,影響了最大值和最小值,那麼結果顯然會發生改變
對於標準化來說:如果出現異常點,由於具有一定資料量,少量的異常點對於平均值的影響並不大,從而方差改變較小。
(3)API
sklearn.preprocessing.StandardScaler( )
處理之後每列來說所有資料都聚集在均值0附近標準差差為1
StandardScaler.fit_transform(X)
X:numpy array格式的資料[n_samples,n_features]
返回值:轉換後的形狀相同的array
(4)資料計算
同樣對上面的資料進行處理
分析
1、範例化StandardScaler
2、通過fit_transform轉換
import pandas as pd
from sklearn.preprocessing import StandardScaler
def stand_demo():
"""
標準化演示
:return: None
"""
data = pd.read_csv("dating.txt")
print(data)
# 1、範例化一個轉換器類
transfer = StandardScaler()
# 2、呼叫fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("標準化的結果:\n", data)
print("每一列特徵的平均值:\n", transfer.mean_)
print("每一列特徵的方差:\n", transfer.var_)
return None
返回結果:
milage Liters Consumtime target
0 40920 8.326976 0.953952 3
1 14488 7.153469 1.673904 2
2 26052 1.441871 0.805124 1
.. ... ... ... ...
997 26575 10.650102 0.866627 3
998 48111 9.134528 0.728045 3
999 43757 7.882601 1.332446 3
[1000 rows x 4 columns]
標準化的結果:
[[ 0.33193158 0.41660188 0.24523407]
[-0.87247784 0.13992897 1.69385734]
[-0.34554872 -1.20667094 -0.05422437]
...,
[-0.32171752 0.96431572 0.06952649]
[ 0.65959911 0.60699509 -0.20931587]
[ 0.46120328 0.31183342 1.00680598]]
每一列特徵的平均值:
[ 3.36354210e+04 6.55996083e+00 8.32072997e-01]
每一列特徵的方差:
[ 4.81628039e+08 1.79902874e+01 2.46999554e-01]
(5)標準化總結
在已有樣本足夠多的情況下比較穩定,適合現代嘈雜巨量資料場景。
2.5 特徵降維
2.5.1 降維
降維是指在某些限定條件下,降低隨機變數(特徵)個數,得到一組「不相關」主變數的過程
降低隨機變數的個數
相關特徵(correlated feature)
相對溼度與降雨量之間的相關
等等
正是因為在進行訓練的時候,我們都是使用特徵進行學習。如果特徵本身存在問題或者特徵之間相關性較強,對於演演算法學習預測會影響較大
2.5.2 降維的兩種方式
特徵選擇
主成分分析(可以理解一種特徵提取的方式)
2.5.3 什麼是特徵選擇
(1)定義
資料中包含冗餘或無關變數(或稱特徵、屬性、指標等),旨在從原有特徵中找出主要特徵。

(2)方法
Filter(過濾式):主要探究特徵本身特點、特徵與特徵和目標值之間關聯
方差選擇法:低方差特徵過濾
相關係數
Embedded (嵌入式):演演算法自動選擇特徵(特徵與目標值之間的關聯)
決策樹:資訊熵、資訊增益
正則化:L1、L2
深度學習:折積等
對於Embedded方式,只能在講解演演算法的時候在進行介紹,更好的去理解
(3)模組
sklearn.feature_selection
(4)過濾式
(4.1) 低方差特徵過濾
刪除低方差的一些特徵,前面講過方差的意義。再結合方差的大小來考慮這個方式的角度。
特徵方差小:某個特徵大多樣本的值比較相近
特徵方差大:某個特徵很多樣本的值都有差別
(4.1.1) API
sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
刪除所有低方差特徵
Variance.fit_transform(X)
X:numpy array格式的資料[n_samples,n_features]
返回值:訓練集差異低於threshold的特徵將被刪除。預設值是保留所有非零方差特徵,即刪除所有樣本中具有相同值的特徵。
(4.1.2) 資料計算
我們對某些股票的指標特徵之間進行一個篩選,資料在"factor_regression_data/factor_returns.csv"檔案當中,除去’index,‘date’,'return’列不考慮(這些型別不匹配,也不是所需要指標)
一共這些特徵
pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense
index,pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense,date,return
0,000001.XSHE,5.9572,1.1818,85252550922.0,0.8008,14.9403,1211444855670.0,2.01,20701401000.0,10882540000.0,2012-01-31,0.027657228229937388
1,000002.XSHE,7.0289,1.588,84113358168.0,1.6463,7.8656,300252061695.0,0.326,29308369223.2,23783476901.2,2012-01-31,0.08235182370820669
2,000008.XSHE,-262.7461,7.0003,517045520.0,-0.5678,-0.5943,770517752.56,-0.006,11679829.03,12030080.04,2012-01-31,0.09978900335112327
3,000060.XSHE,16.476,3.7146,19680455995.0,5.6036,14.617,28009159184.6,0.35,9189386877.65,7935542726.05,2012-01-31,0.12159482758620697
4,000069.XSHE,12.5878,2.5616,41727214853.0,2.8729,10.9097,81247380359.0,0.271,8951453490.28,7091397989.13,2012-01-31,-0.0026808154146886697
分析
1、初始化VarianceThreshold,指定閥值方差
2、呼叫fit_transform
def variance_demo():
"""
刪除低方差特徵——特徵選擇
:return: None
"""
data = pd.read_csv("factor_returns.csv")
print(data)
# 1、範例化一個轉換器類
transfer = VarianceThreshold(threshold=1)
# 2、呼叫fit_transform
data = transfer.fit_transform(data.iloc[:, 1:10])
print("刪除低方差特徵的結果:\n", data)
print("形狀:\n", data.shape)
return None
返回結果:
index pe_ratio pb_ratio market_cap \
0 000001.XSHE 5.9572 1.1818 8.525255e+10
1 000002.XSHE 7.0289 1.5880 8.411336e+10
... ... ... ... ...
2316 601958.XSHG 52.5408 2.4646 3.287910e+10
2317 601989.XSHG 14.2203 1.4103 5.911086e+10
return_on_asset_net_profit du_return_on_equity ev \
0 0.8008 14.9403 1.211445e+12
1 1.6463 7.8656 3.002521e+11
... ... ... ...
2316 2.7444 2.9202 3.883803e+10
2317 2.0383 8.6179 2.020661e+11
earnings_per_share revenue total_expense date return
0 2.0100 2.070140e+10 1.088254e+10 2012-01-31 0.027657
1 0.3260 2.930837e+10 2.378348e+10 2012-01-31 0.082352
2 -0.0060 1.167983e+07 1.203008e+07 2012-01-31 0.099789
... ... ... ... ... ...
2315 0.2200 1.789082e+10 1.749295e+10 2012-11-30 0.137134
2316 0.1210 6.465392e+09 6.009007e+09 2012-11-30 0.149167
2317 0.2470 4.509872e+10 4.132842e+10 2012-11-30 0.183629
[2318 rows x 12 columns]
刪除低方差特徵的結果:
[[ 5.95720000e+00 1.18180000e+00 8.52525509e+10 ..., 1.21144486e+12
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 1.58800000e+00 8.41133582e+10 ..., 3.00252062e+11
2.93083692e+10 2.37834769e+10]
[ -2.62746100e+02 7.00030000e+00 5.17045520e+08 ..., 7.70517753e+08
1.16798290e+07 1.20300800e+07]
...,
[ 3.95523000e+01 4.00520000e+00 1.70243430e+10 ..., 2.42081699e+10
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 2.46460000e+00 3.28790988e+10 ..., 3.88380258e+10
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 1.41030000e+00 5.91108572e+10 ..., 2.02066110e+11
4.50987171e+10 4.13284212e+10]]
形狀:
(2318, 8)
4.2 相關係數
皮爾遜相關係數(Pearson Correlation Coefficient)
反映變數之間相關關係密切程度的統計指標
4.2.2 公式計算案例(瞭解,不用記憶)
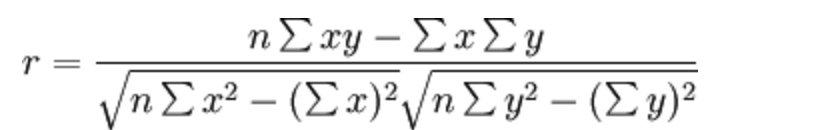
比如說我們計算年廣告費投入與月均銷售額
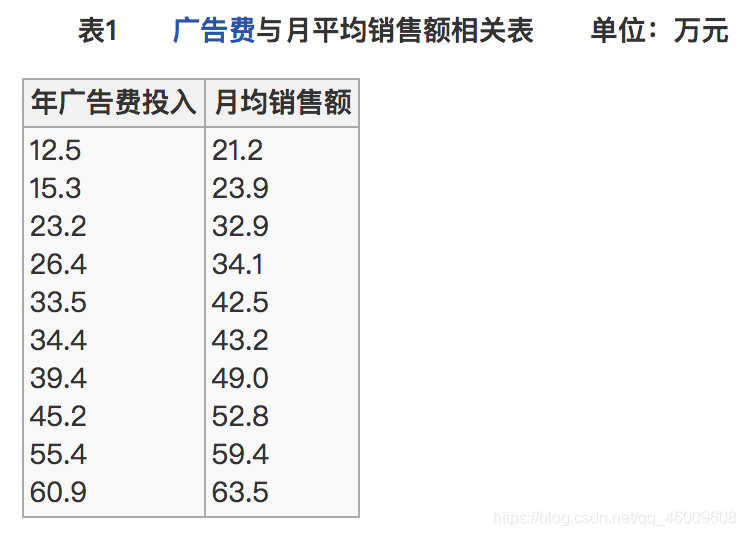
那麼之間的相關係數怎麼計算
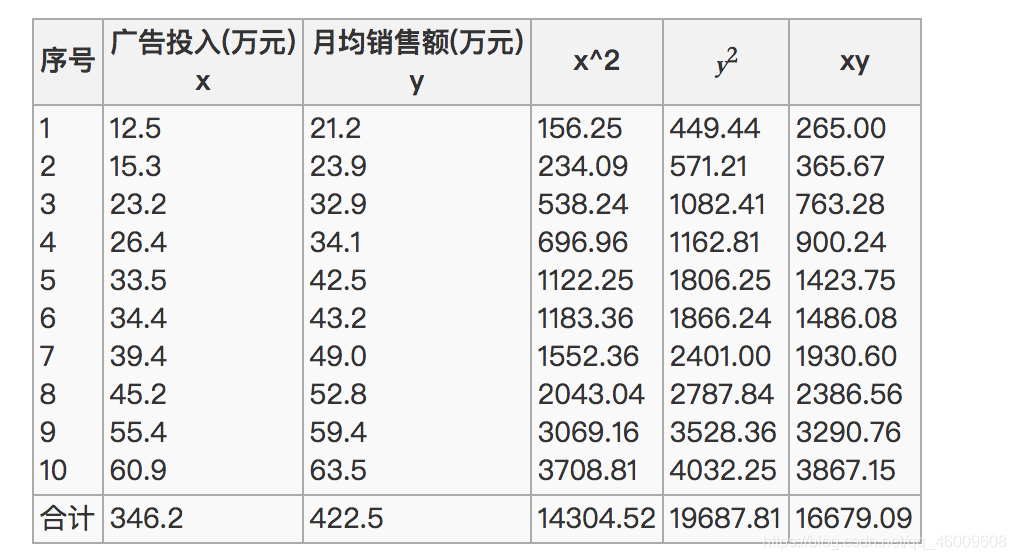
最終計算:
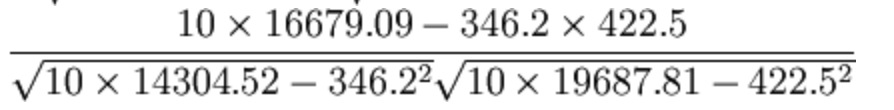
= 0.9942
所以我們最終得出結論是廣告投入費與月平均銷售額之間有高度的正相關關係。
4.2.3 特點
相關係數的值介於–1與+1之間,即–1≤ r ≤+1。其性質如下:
- 當r>0時,表示兩變數正相關,r<0時,兩變數為負相關
- 當|r|=1時,表示兩變數為完全相關,當r=0時,表示兩變數間無相關關係
- 當0<|r|<1時,表示兩變數存在一定程度的相關。且|r|越接近1,兩變數間線性關係越密切;|r|越接近於0,表示兩變數的線性相關越弱
- 一般可按三級劃分:|r|<0.4為低度相關;0.4≤|r|<0.7為顯著性相關;0.7≤|r|<1為高度線性相關
這個符號:|r|為r的絕對值, |-5| = 5
4.2.4 API
from scipy.stats import pearsonr
x : (N,) array_like
y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)
4.2.5 案例:股票的財務指標相關性計算
我們剛才的股票的這些指標進行相關性計算, 假設我們以
factor = ['pe_ratio','pb_ratio','market_cap','return_on_asset_net_profit','du_return_on_equity','ev','earnings_per_share','revenue','total_expense']
這些特徵當中的兩兩進行計算,得出相關性高的一些特徵
分析
兩兩特徵之間進行相關性計算
import pandas as pd
from scipy.stats import pearsonr
def pearsonr_demo():
"""
相關係數計算
:return: None
"""
data = pd.read_csv("factor_returns.csv")
factor = ['pe_ratio', 'pb_ratio', 'market_cap', 'return_on_asset_net_profit', 'du_return_on_equity', 'ev',
'earnings_per_share', 'revenue', 'total_expense']
for i in range(len(factor)):
for j in range(i, len(factor) - 1):
print(
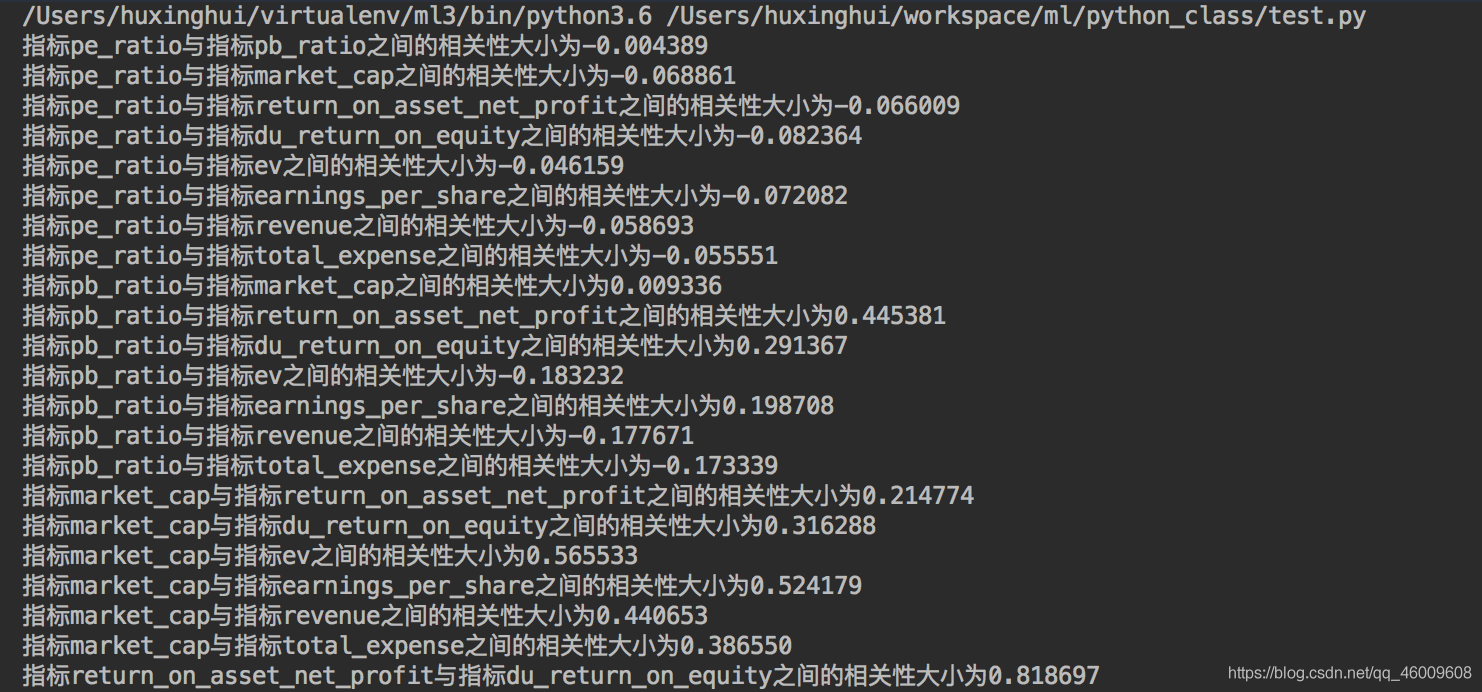
"指標%s與指標%s之間的相關性大小為%f" % (factor[i], factor[j + 1], pearsonr(data[factor[i]], data[factor[j + 1]])[0]))
return None
返回結果:
指標pe_ratio與指標pb_ratio之間的相關性大小為-0.004389
指標pe_ratio與指標market_cap之間的相關性大小為-0.068861
指標pe_ratio與指標return_on_asset_net_profit之間的相關性大小為-0.066009
指標pe_ratio與指標du_return_on_equity之間的相關性大小為-0.082364
指標pe_ratio與指標ev之間的相關性大小為-0.046159
指標pe_ratio與指標earnings_per_share之間的相關性大小為-0.072082
指標pe_ratio與指標revenue之間的相關性大小為-0.058693
指標pe_ratio與指標total_expense之間的相關性大小為-0.055551
指標pb_ratio與指標market_cap之間的相關性大小為0.009336
指標pb_ratio與指標return_on_asset_net_profit之間的相關性大小為0.445381
指標pb_ratio與指標du_return_on_equity之間的相關性大小為0.291367
指標pb_ratio與指標ev之間的相關性大小為-0.183232
指標pb_ratio與指標earnings_per_share之間的相關性大小為0.198708
指標pb_ratio與指標revenue之間的相關性大小為-0.177671
指標pb_ratio與指標total_expense之間的相關性大小為-0.173339
指標market_cap與指標return_on_asset_net_profit之間的相關性大小為0.214774
指標market_cap與指標du_return_on_equity之間的相關性大小為0.316288
指標market_cap與指標ev之間的相關性大小為0.565533
指標market_cap與指標earnings_per_share之間的相關性大小為0.524179
指標market_cap與指標revenue之間的相關性大小為0.440653
指標market_cap與指標total_expense之間的相關性大小為0.386550
指標return_on_asset_net_profit與指標du_return_on_equity之間的相關性大小為0.818697
指標return_on_asset_net_profit與指標ev之間的相關性大小為-0.101225
指標return_on_asset_net_profit與指標earnings_per_share之間的相關性大小為0.635933
指標return_on_asset_net_profit與指標revenue之間的相關性大小為0.038582
指標return_on_asset_net_profit與指標total_expense之間的相關性大小為0.027014
指標du_return_on_equity與指標ev之間的相關性大小為0.118807
指標du_return_on_equity與指標earnings_per_share之間的相關性大小為0.651996
指標du_return_on_equity與指標revenue之間的相關性大小為0.163214
指標du_return_on_equity與指標total_expense之間的相關性大小為0.135412
指標ev與指標earnings_per_share之間的相關性大小為0.196033
指標ev與指標revenue之間的相關性大小為0.224363
指標ev與指標total_expense之間的相關性大小為0.149857
指標earnings_per_share與指標revenue之間的相關性大小為0.141473
指標earnings_per_share與指標total_expense之間的相關性大小為0.105022
指標revenue與指標total_expense之間的相關性大小為0.995845
從中我們得出
指標revenue與指標total_expense之間的相關性大小為0.995845
指標return_on_asset_net_profit與指標du_return_on_equity之間的相關性大小為0.818697
我們也可以通過畫圖來觀察結果
import matplotlib.pyplot as plt
plt.figure(figsize=(20, 8), dpi=100)
plt.scatter(data['revenue'], data['total_expense'])
plt.show()
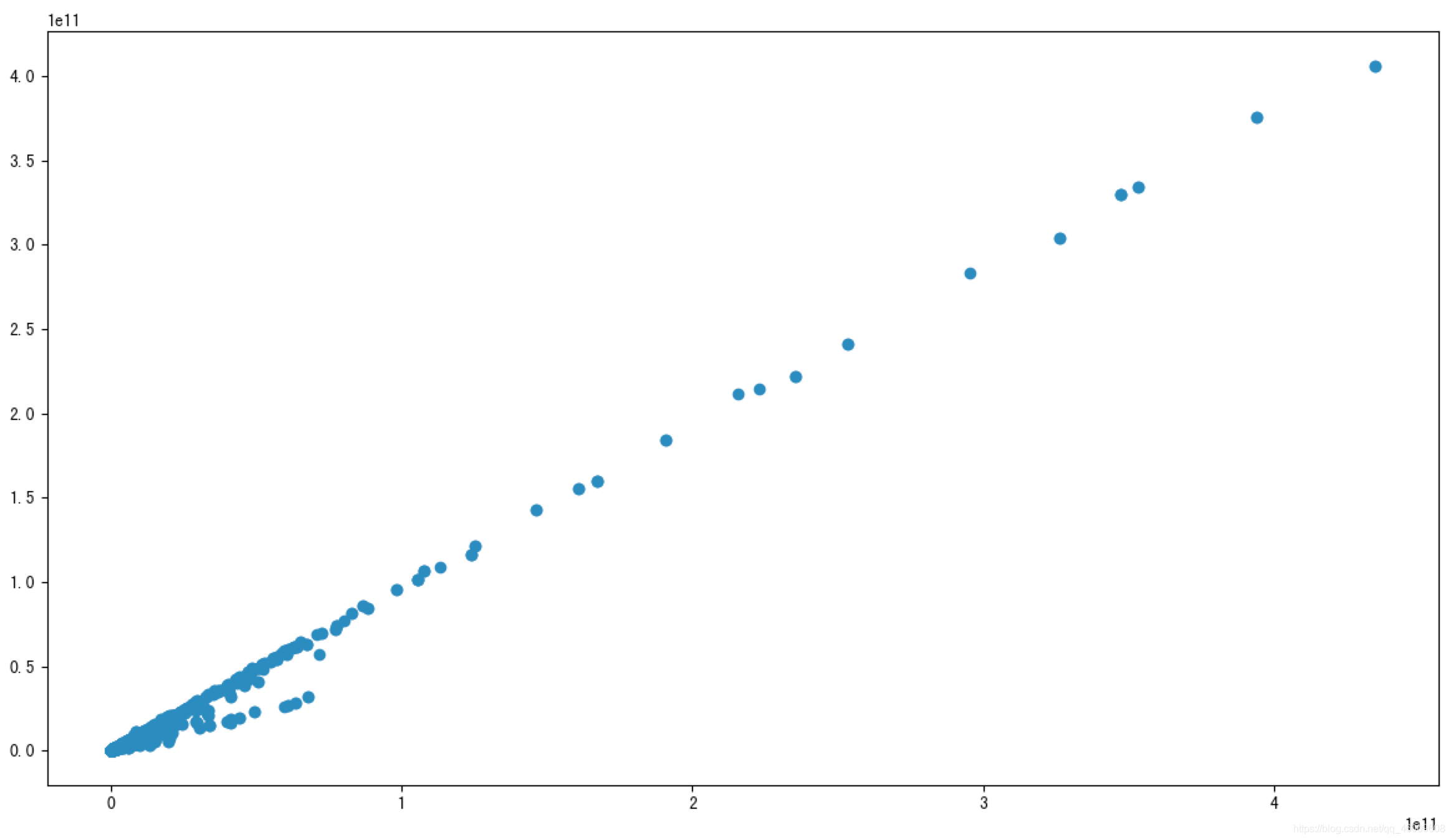
這兩對指標之間的相關性較大,可以做之後的處理,比如合成這兩個指標。
2.6 主成分分析
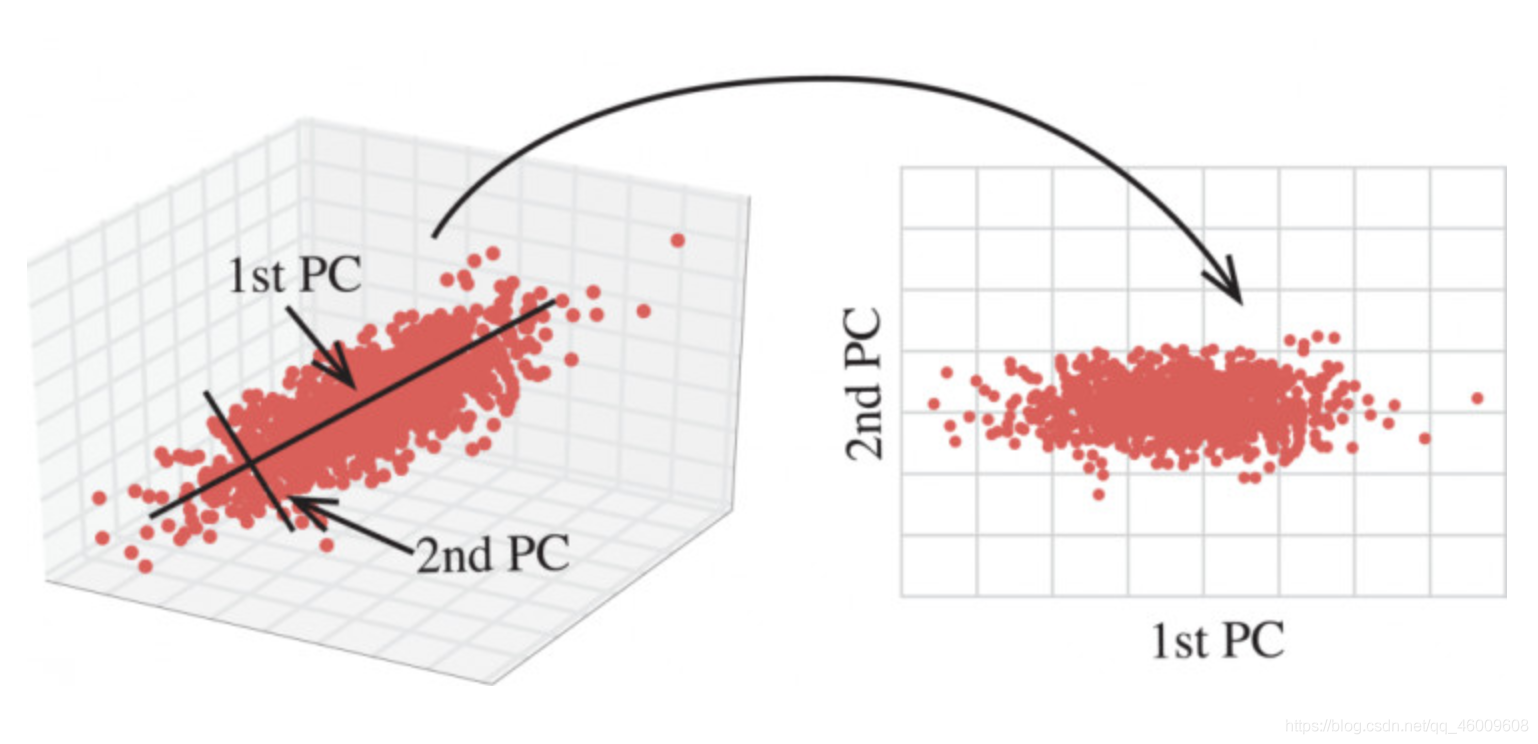
2.6.1 什麼是主成分分析(PCA)
- 定義:高維資料轉化為低維資料的過程,在此過程中可能會捨棄原有資料、創造新的變數
- 作用:是資料維數壓縮,儘可能降低原資料的維數(複雜度),損失少量資訊。
- 應用:迴歸分析或者聚類分析當中
那麼更好的理解這個過程呢?我們來看一張圖

(1)計算案例理解(瞭解,無需記憶)
假設對於給定5個點,資料如下
(-1,-2)
(-1, 0)
( 0, 0)
( 2, 1)
( 0, 1)
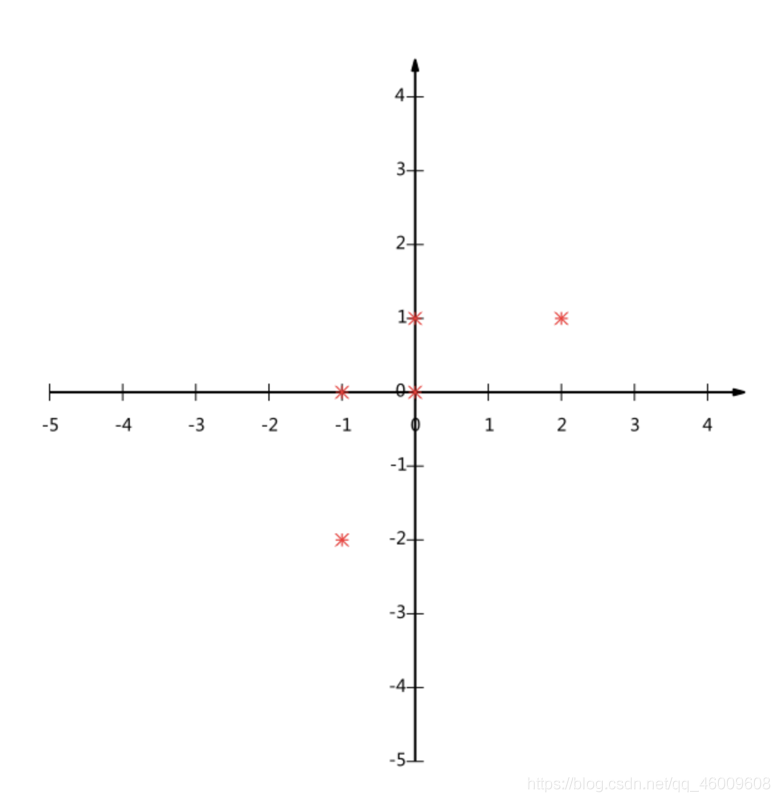
要求:將這個二維的資料簡化成一維? 並且損失少量的資訊
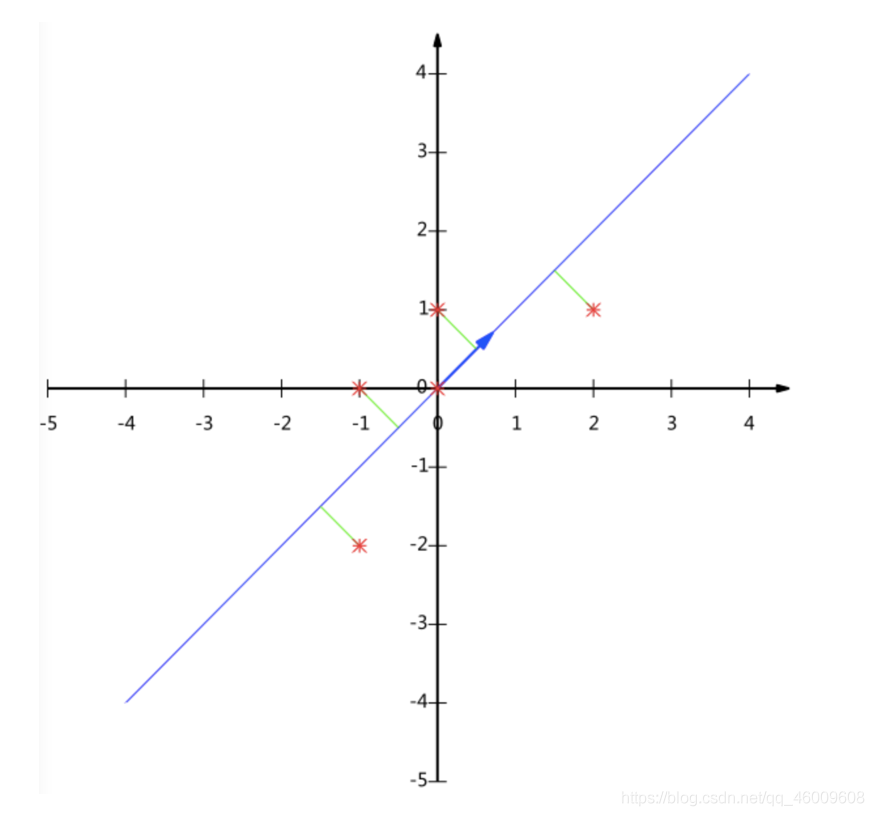
這個過程如何計算的呢?找到一個合適的直線,通過一個矩陣運算得出主成分分析的結果(不需要理解)

(2)API
sklearn.decomposition.PCA(n_components=None)
將資料分解為較低維數空間
n_components:
小數:表示保留百分之多少的資訊;
整數:減少到多少特徵。
PCA.fit_transform(X) X:numpy array格式的資料[n_samples,n_features]
返回值:轉換後指定維度的array
(3)資料計算
先拿個簡單的資料計算一下
[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]
from sklearn.decomposition import PCA
def pca_demo():
"""
對資料進行PCA降維
:return: None
"""
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
# 1、範例化PCA, 小數——保留多少資訊
transfer = PCA(n_components=0.9)
# 2、呼叫fit_transform
data1 = transfer.fit_transform(data)
print("保留90%的資訊,降維結果為:\n", data1)
# 1、範例化PCA, 整數——指定降維到的維數
transfer2 = PCA(n_components=3)
# 2、呼叫fit_transform
data2 = transfer2.fit_transform(data)
print("降維到3維的結果:\n", data2)
return None
返回結果:
保留90%的資訊,降維結果為:
[[ -3.13587302e-16 3.82970843e+00]
[ -5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
降維到3維的結果:
[[ -3.13587302e-16 3.82970843e+00 4.59544715e-16]
[ -5.74456265e+00 -1.91485422e+00 4.59544715e-16]
[ 5.74456265e+00 -1.91485422e+00 4.59544715e-16]]
2.6.2 案例:探究使用者對物品類別的喜好細分降維

資料如下:
order_products__prior.csv:訂單與商品資訊
欄位:order_id, product_id, add_to_cart_order, reordered
products.csv:商品資訊
欄位:product_id, product_name, aisle_id, department_id
orders.csv:使用者的訂單資訊
欄位:order_id,user_id,eval_set,order_number,….
aisles.csv:商品所屬具體物品類別
欄位: aisle_id, aisle
(1)需求
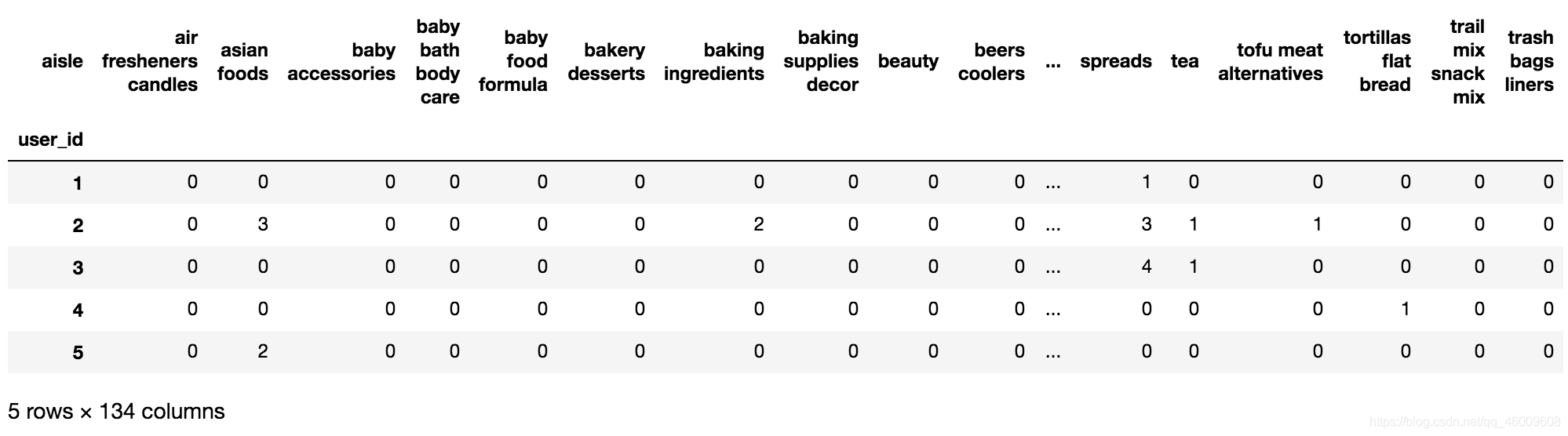
(2)分析
- 合併表,使得user_id與aisle在一張表當中
- 進行交叉表變換
- 進行降維
(3)完整程式碼
import pandas as pd
from sklearn.decomposition import PCA
# 1、獲取資料集
# ·商品資訊- products.csv:
# Fields:product_id, product_name, aisle_id, department_id
# ·訂單與商品資訊- order_products__prior.csv:
# Fields:order_id, product_id, add_to_cart_order, reordered
# ·使用者的訂單資訊- orders.csv:
# Fields:order_id, user_id,eval_set, order_number,order_dow, order_hour_of_day, days_since_prior_order
# ·商品所屬具體物品類別- aisles.csv:
# Fields:aisle_id, aisle
products = pd.read_csv("./instacart/products.csv")
order_products = pd.read_csv("./instacart/order_products__prior.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")
# 2、合併表,將user_id和aisle放在一張表上
# 1)合併orders和order_products on=order_id tab1:order_id, product_id, user_id
tab1 = pd.merge(orders, order_products, on=["order_id", "order_id"])
# 2)合併tab1和products on=product_id tab2:aisle_id
tab2 = pd.merge(tab1, products, on=["product_id", "product_id"])
# 3)合併tab2和aisles on=aisle_id tab3:user_id, aisle
tab3 = pd.merge(tab2, aisles, on=["aisle_id", "aisle_id"])
# 3、交叉表處理,把user_id和aisle進行分組
table = pd.crosstab(tab3["user_id"], tab3["aisle"])
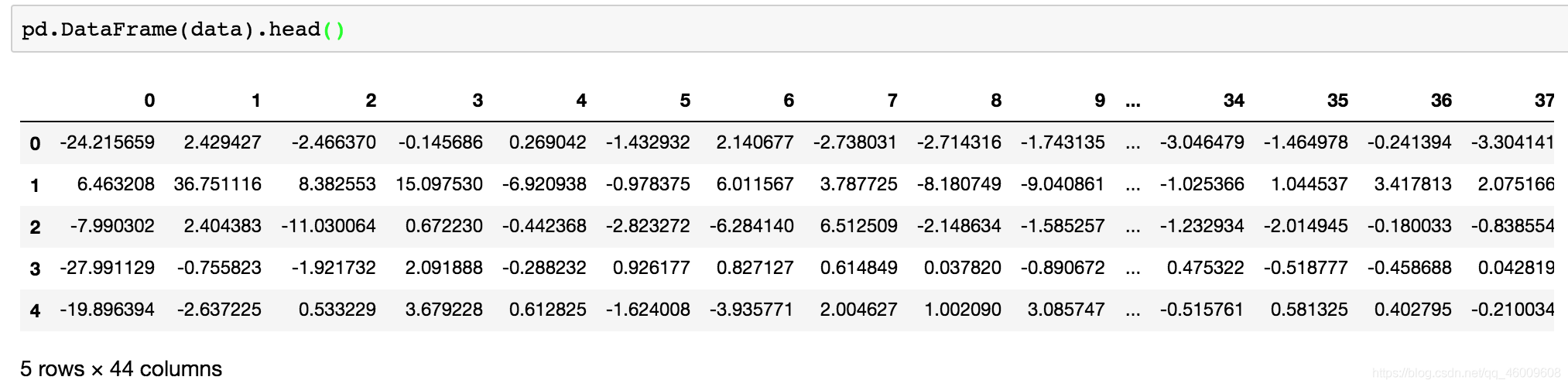
# 4、主成分分析的方法進行降維
# 1)範例化一個轉換器類PCA
transfer = PCA(n_components=0.95)
# 2)fit_transform
data = transfer.fit_transform(table)
data.shape
返回結果:
(206209, 44)
總結:
1、資料集的結構是什麼?
答案: 特徵值+ 目標值
2、機器學習演演算法分成哪些類別? 如何分類
答案: 根據是否有目標值分為 監督學習和非監督學習監督學習
根據目標值的資料型別:目標值為離散值就是分類問題
目標值為連續值就是迴歸問題
3、什麼是標準化? 和歸一化相比有什麼優點?
答案: 標準化是通過對原始資料進行變換把資料變換到均值為0,方差為1範圍內
優點: 少量異常點, 不影響平均值和方差, 對轉換影響小