2020 CCPC 秦皇島站 Promble G. Good number

2020 CCPC 秦皇島站 Promble G. Good number

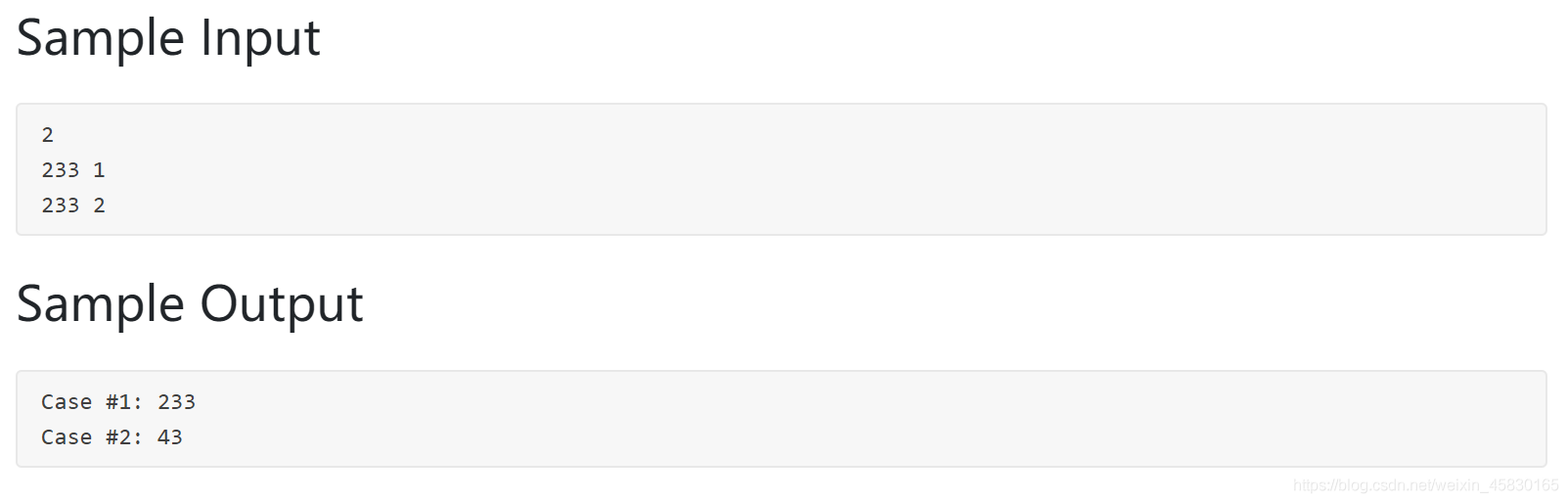
題意：

一個正整數x，當且僅當x開k次方（向下取整）整除x時，即x/x^1/k，x為一個good number。現給定一個整數n，求1到n之間有多少個good number？

分析：

這道題運用到了分塊，
通過判斷得出，k分為三種情況：

1.當k=1時，即x除以x本身，1到n間所有數位都能滿足good number,輸出n

2.當k<=31時（以k=2為例）
我們可以把x分為多個塊，劃分依據為x開k次方後向下取整的結果是否相同

當x∈[1,3]時，開k次方後向下取整，結果都為1，能被1整除的數：1，2，3 即數目為：3
當x∈[4,8]時，開k次方後向下取整，結果都為2，能被2整除的數：4，6，8 即數目為3
當x∈[9,15]時，開k次方後向下取整，結果都為3，能被3整除的數：9，12，15 即數目為3
當x∈[16,24]時，開k次方後向下取整，結果都為4，能被4整除的數：16，20，24 即數目為3
當x∈[25,35]時，開k次方後向下取整，結果都為5，能被5整除的數：25，30，35 即數目為3
……
我們可以發現規律，
數目=（塊的最後一個數-塊的第一個數）/x開方取整後的數+1

3.當k>32時, 因為2³²=4294967296>10⁹, x開k次方後為1,所以1到n間所有數位都滿足good number,輸出n

程式碼：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//快速冪
ll fun(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans*=a;
        a*=a;
        b>>=1;
    }
    return ans;
}
int main()
{
    int t,arr,brr;
    ll n,k;
    cin>>t;
    for(int i=1;i<=t;i++)
    {
        ll ans=0;
        scanf("%lld%lld",&n,&k);
        if(k==1||k>=31)//當k=1,或k>=31時，開k次方後只能為1，所有數都可以整除
        {
            printf("Case #%d: %lld\n",i,n);
            continue;
        }
        else
        {
            for(int j=1;fun(j,k)<=n;j++)//j:x開方向下取整後的數
            {
                 arr=fun(j,k);//次方數，即每個塊的第一個數
                 brr=min(n,fun(j+1,k));//判斷塊是否越界，brr:下一個塊的第一個數
                 ans+=(brr-1-arr)/j+1;//brr-1:每塊的最後一個數，j~arr間的數為底數相同的塊
            }
            printf("Case #%d: %lld\n",i,ans);
        }
    }
    return 0;
}

結果：