杭電 oj 1006 Tick and Tick 個人題解

首先貼上官網原題

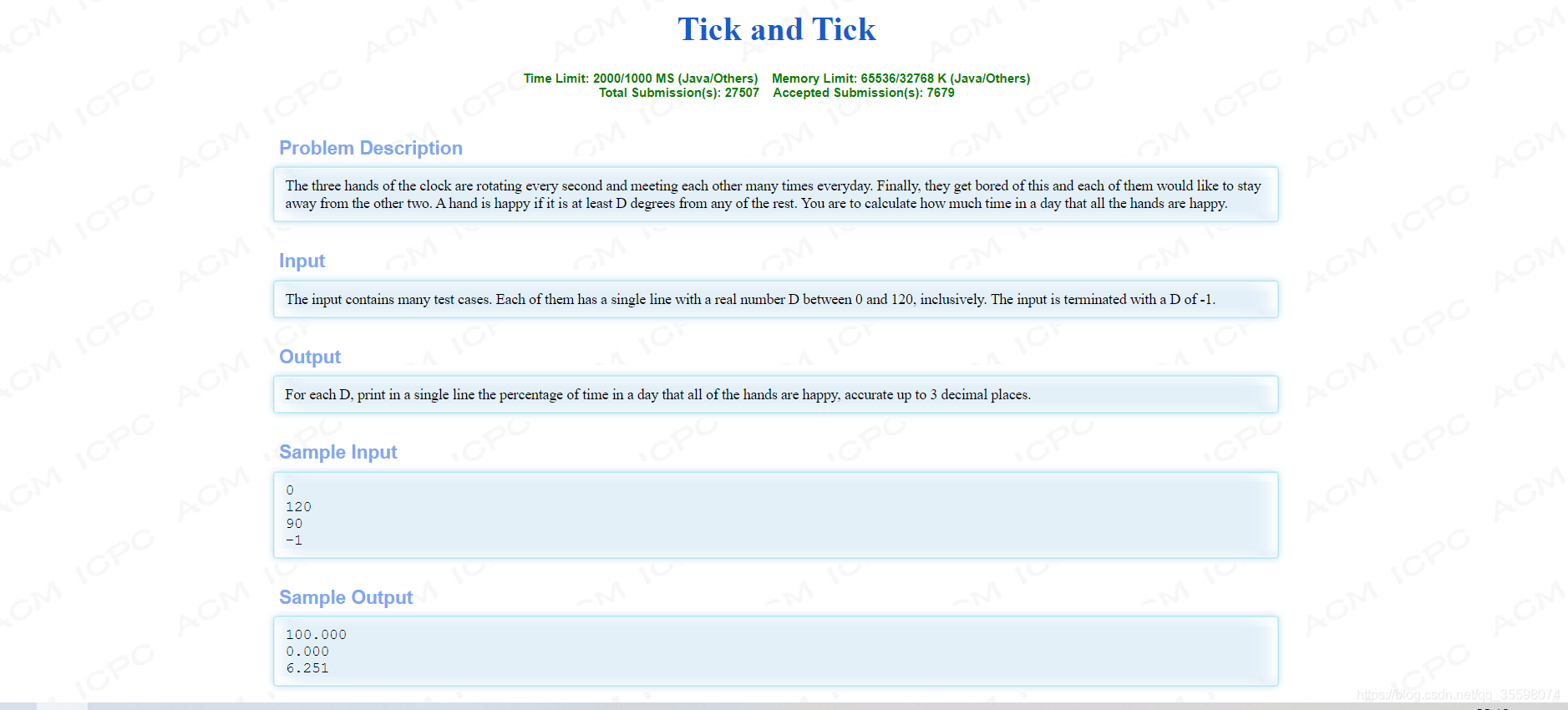
剛開始看到這道題覺得又是一道水題，後面仔細看了一下題目後才知道這道題更加考數學，確實讓我糾結了很久。以下是我的一些思路：

思路一：暴力模擬法

可能一般人都會用秒數來模擬時鐘，然後根據秒數來確定時針和分針的位置，然後累加時間，這裡可以用1s,0.1s，0.01s,甚至是0.001s來作為單位時間模擬，但其實有兩大缺點：
1. 單位時間小，要模擬的次數多。
2. 精度不夠，要保留小數點後3位。
我用的不是秒數模擬，而是用秒針所走過的度數來模擬，這樣可以省去時間與度數的轉換。
需要知道的是：秒針的速度=60×分針的速度=720×時針的速度
這裡先貼上我寫的程式碼（作為第一種思路提交的，oj上失敗了）：

#include<bits/stdc++.h>//這個標頭檔案也稱萬能頭,包括c和c++的很多標頭檔案
using namespace std;
int main()
{
    int n;
    double a=0,t=0,miao,fen,shi;
    cin>>n;
    while(n<=120&&n>=0)
    {
        //模擬時鐘
        while(shi<360)
        {
            t+=0.45;//t是計算總時間，以0.45°為單位累加
            miao=t-(int)t/360*360;//這裡因為t為double型，用不了%，所以自己寫了一個類似與%的東西。
            fen=t/60-(int)t/60/360*360;
            shi=t/720;
            if(abs(miao-fen)>=n&&miao-fen+360>=n&&fen+360-miao>=n)//這裡的判斷略顯繁瑣，其實可以用define宏來簡化程式碼。
               if(abs(miao-shi)>=n&&miao-shi+360>=n&&shi+360-miao>=n)
                  if(abs(fen-shi)>=n&&fen-shi+360>=n&&shi+360-fen>=n)
                     a+=0.45;//a用來統計開心時間
        }
        printf("%.3lf\n",a/t*100);//c++的小數點控制不大會用，方便起見用了c的printf函數
        cin>>n;
        a=t=shi=0;//這裡需要重置資料
    }
    cin.get();
    cin.get();//這裡用兩個cin.get();來暫停介面,保留視窗,不影響oj的判斷
}

這裡其實有很多細節處理過程，
如：3個if的寫法，舉其中一例，abs(miao-fen)>=n,是判斷miao和fen的度數之差，這裡用abs是因為fen的度數有可能超過miao(相對與起始位置)。還有就是後面的(miao-fen+360)>=n和fen-miao+360是用來算另一個夾角的。

然後這個0.45也是偵錯過好幾遍，剛開始用的是0.01，執行後發現執行時間太長了，就把它改大了一些，變成1，雖然測試樣例對了，但是提交上去的時候就錯了(精度不夠）。
貼上提交的圖：

這裡可以看到答案錯誤，而且執行時間還不小。
所以我嘗試著用時間來換精度。
結果如圖所示：


然後嘗試著調大一些，調成0.5:

在調小一些（心累），0.45：

事實證明：沒有好的演演算法oj不認！
所以我就開始百度，發現很多其他博主用的是解方程的形式, 但也都是程式碼一貼，看不懂，或者太長了不想看，本來想著要放棄，但是後來想想不會的題目不去做永遠不會，還不如再試試。
今天費了整天，終於死磕出來，也就是思路2。

思路2:解方程,算符合條件的兩兩之間的區間,最後取交集,合併區間。

閒談:

先說說我的整個掙扎的過程(不想看的可以直接跳過,博主個人的廢話):
開始,我想的是用做數學題的想法,就是先讓分針和時針先產生一個n的夾角,算出此時的時間,然後再在此基礎之上去確定秒針的位置,這裡貼一下我半途而廢的程式碼:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,q=0;
    double miao=0,fen,shi,t1,t2,t3,t4,ans=0;
    cin>>n;
    while(n<=120&&n>=0)
    {
        //解多次方程
        while(720/11*(n+q*360)<259200)//用度數來解方程
        {
           t1=720/11*(n+q*360);q++;//解出分針與時針滿足條件時的時間
           t2=720/11*(q*360-n);//t1,t2用來確定分針和時針開心的邊界,t3,t4用來確定秒針分別與時針和分針的開心邊界
           //用for迴圈尋找在t1-t2該區間的miao的範圍
           t3=t4=0;
           
 
           for(int i=0;t3<259200;i++)
           {
               t3=(n+(i*360))*720/719;
               if(t1<t3&&t3<t2)break;
           }
           for(int i=0;t4<259200;i++)
           {
               t4=(360*(i+1)-n)*720/719;
           }      
        }
        
    }
    cin.get();
    cin.get();
}

但後來才發現不對,t3和t4那個在前面,那個後面呢?t3和t4還要去公共部分,可能會與上一個t3或者上一個t4 時間有重疊等等…
所以,我決定用計算機特性:能夠儲存大量資料,來解決所有頭疼的問題

正題:

其實回過頭來看這道題會發現,無非他讓我們做的不就是算出所有滿足條件的時間區間,然後相加,最後計算佔總時間的比例.
因為一天24小時前12個小時和後12個小時情況相同,所以就用12個小時為總時間.
首先,對於這道題總的框架應該是先計算兩兩直接滿足條件的區間(你也不可能一次性把三個條件全滿足的區間算出來)
所以應當是算時針和秒針的區間,時針和分針的區間,以及分針和時針的區間,最後取交集.
先貼上程式碼再說明:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,s1=0,s2=0,s3=0,s4=0;
    double ms[2000],fs[30],fm[2000],h1[2000],ans=0;
    cin>>n;
    while(n<=120&&n>=0)
    {
        for(int i=0;(n+360*i)*720.0/719<259200;i++)
        {
            ms[s1++]=(n+360*i)*720.0/719;
            ms[s1++]=((i+1)*360-n)*720.0/719;
        }

        for(int i=0;(n+360*i)*720.0/11<259200;i++)
        {
            fs[s2++]=(n+360*i)*720.0/11;
            fs[s2++]=((i+1)*360-n)*720.0/11;
        }

        for(int i=0;(n+360*i)*60.0/59<259200;i++)
        {
            fm[s3++]=(n+360*i)*60.0/59;
            fm[s3++]=((i+1)*360-n)*60.0/59;
        }
        //合併fs和fm,併入h1之中
        for(int i=0;i<s2;i+=2)
          for(int j=0;j<s3&&fm[j]<fs[i+1];j+=2)
          {
              if(fm[j+1]>fs[i])
              {
                  h1[s4++]=max(fm[j],fs[i]);
                  h1[s4++]=min(fm[j+1],fs[i+1]);
              }
          }
        //合併h1和ms,併入fm
        s3=0;
        for(int i=0;i<s4;i+=2)
        for(int j=0;j<s1&&ms[j]<h1[i+1];j+=2)
        {
            if(ms[j+1]>h1[i])
            {
                fm[s3++]=max(ms[j],h1[i]);
                fm[s3++]=min(ms[j+1],h1[i+1]);
            }
        }
        for(int i=0;i<s3;i+=2)ans+=fm[i+1]-fm[i];
        printf("%.3f\n",ans/259200*100);
        s1=s2=s3=s4=ans=0;
        cin>>n;
    }
    cin.get();
    cin.get();
}

1.
int型:
n 用來儲存輸入資料
s1 用來儲存ms陣列的元素個數(預計有1440,保險起見用2000個)
s2 儲存fs陣列的元素個數(預計24個,用30)
s3 儲存fm陣列的元素個數(預計1440個,用2000)
s4 儲存h1陣列的元素個數(預計1440個,用2000)
2.
double陣列:
ms陣列存的是秒針和時針滿足條件的區間(ms是秒時的縮寫)
以此類推
h1陣列用來存第一次合併的區間(兩兩合併要2次,本來要有2個陣列來存合併區間,但是我是先把fs和fm合併的,所以第二次合併的時候fm陣列沒用,可以空出來當最終的區間陣列,另外主要是fs陣列的值很少,先合併fs陣列可以少迴圈幾次)
double ans用來儲存開心時間.
3.(最核心的部分)
如何算即如何解方程?

其實很簡單,我們先以n=90°,秒針和時針為例,我這裡用的是度數列的方程,即設秒針走過的度數為x,則第一次滿足條件時:
x-x/720=90
那秒針再超過時針一圈呢?
x-x/720=90+360
再來一圈呢?
x-x/720=90+360×2
…
x-x/720=90+360×i
那麼解得x=(90+360×i)×720/719.

其實還有一種情況:
還是時針和秒針
當秒針超過時針並去追時針時,第一次滿足條件時有:
x/720+360-x=90
同理i圈後:
x/720+360×i-x=90
解得x=(360×i-90)×720/719.

那麼可以以此類推秒針和分針,分針和時針的情況.
最後再兩兩合併,累加時間ans.然後輸出比例後記得重置資料,以便下一次的運算.

(PS:評論支援一下博主,深夜12:30了,有點困了~ )

附上我的草稿(亂的一)