AC自動機:如何實現敏感詞過濾?
敏感詞過濾
在一些社交平臺如微博、微信、網路遊戲等地方,難免會有一些不法分子散播色情、反動等內容,亦或是網友們的互相謾罵、騷擾等。為了淨化網路環境,各大社交平臺中都會有敏感詞過濾的機制,將那些不好的詞彙遮蔽或者替換掉
那你是否有想過,這個功能是如何實現的呢?
在我之前的部落格中,介紹了四種單模式字串匹配演演算法,分別是BF、RK、BM、KMP,以及一種多模式字串匹配演演算法,Trie樹。
對於單模式字串匹配演演算法來說,如果我們要進行匹配,就需要針對每一個查詢詞來對我們輸入的主串進行匹配,而隨著詞庫的增大,匹配的次數也會變得越來越大,很顯然,這種做法是行不通的。
那麼我們再看看多模式字串匹配演演算法,Trie樹。對於Trie樹來說,我們可以一次性將所有的敏感詞都加入其中,然後再遍歷主串,在樹中查詢匹配的字串,如果找不到,則使Trie樹重新回到根節點,再從主串的下一個位置開始找起。
Trie樹的這種方法,就有點像BF中的暴力匹配,因為它沒有一個合理的減少比較的機制,每當我們不匹配就需要從頭開始查,大大的降低了執行的效率,對於一個高流量的社交平臺來說這是不能容許的,畢竟沒有人希望自己輸入了一句話後要隔上一大段時間才能發出去。那麼我們是否可以效仿KMP演演算法,新增一個類似next陣列的機制來減少不必要的匹配呢?這也就是AC自動機的由來
AC自動機
AC自動機全程是Aho-CorasickAutoMaton,和Trie樹一樣是多模式字串匹配演演算法。並且它與Trie樹的關係就相當於KMP與BF演演算法的關係一樣,AC自動機的效率要遠遠超出Trie樹
AC自動機對Trie進行了改進,在Trie的基礎上結合了KMP演演算法的思想,在樹中加入了類似next陣列的失效指標。
struct ACNode
{
char _data; //當前字元
bool _isEnd; //標記當前是否能構成一個單詞
int _length; //當前模式串長度
ACNode* _fail; //失敗指標
unordered_map<char, ACNode*> _subNode; //子節點
};
AC自動機的構建主要包含以下兩個操作
- 將多個模式串構建成Trie樹
- 為Trie樹中每個節點構建失敗指標
上述兩個步驟看起來簡單,但是理解起來十分複雜,如果不瞭解KMP演演算法和Trie樹的話很難搞懂,所以如果對這兩方面知識不熟的可以看看我往期的部落格
在本篇部落格中不會再次介紹KMP和Trie,如果需要了解的可以看看我的往期部落格
Trie(字典樹) : 如何實現搜尋引擎的關鍵詞提示功能?
字串匹配演演算法(三):KMP(KnuthMorrisPratt)演演算法
失效指標
例如我們具有這麼一棵樹
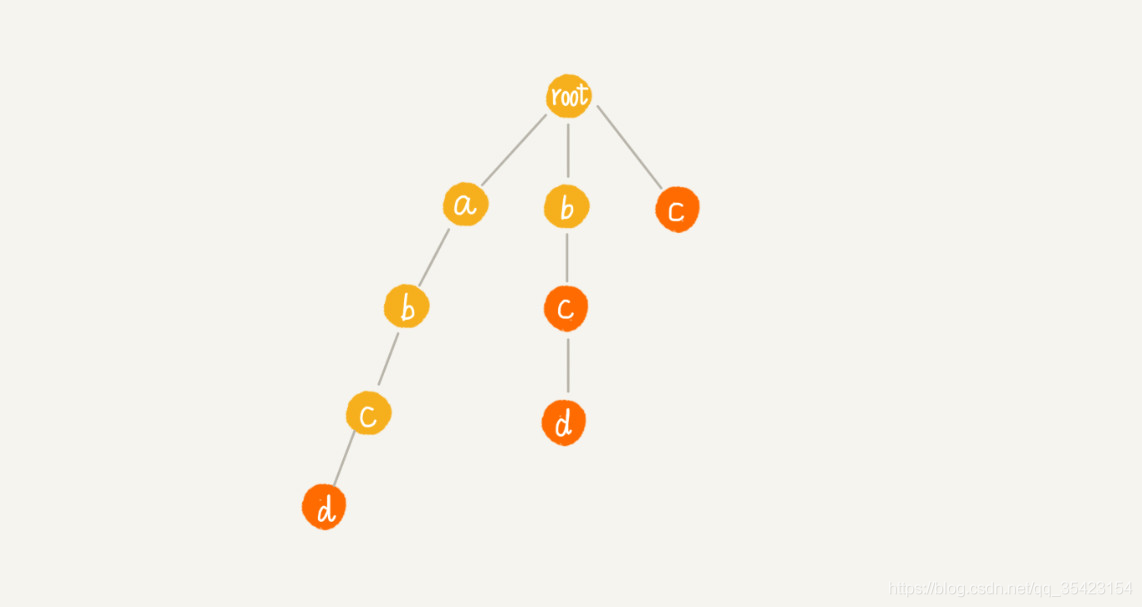
如果要儘量減少匹配,我們就可以藉助之前KMP的思想,通過找到可匹配的字尾子串或者字首子串,將其對其,就可以減少中間多餘的比對。
又由於Trie樹是通過字元來劃分子樹,所以基於字首的匹配不太容易理想(同一字首的在同一條路徑下,滑動效率不高),那麼我們就可以選擇通過字尾來進行比對。
所以我們失敗節點即為我們對其的位置,它的值與本節點值相同,並且失敗指標指向的節點所構成的單詞就是我們的字尾
首先,由於根節點不存資料,並且其沒有父節點,所以它的失敗指標為空。而我們又是基於字元劃分的,所以在同一層中不可能有相同的節點,相同節點只能出現在相鄰層中,並且我們又需要保證具有相同的字尾,所以得出結論,某個節點的失敗指標只可能存在它的上層中。
基於以上兩個特點,我們就可以直接推匯出第一層節點的失敗指標都為root。接著繼續思考,如何構建下面的失敗節點。
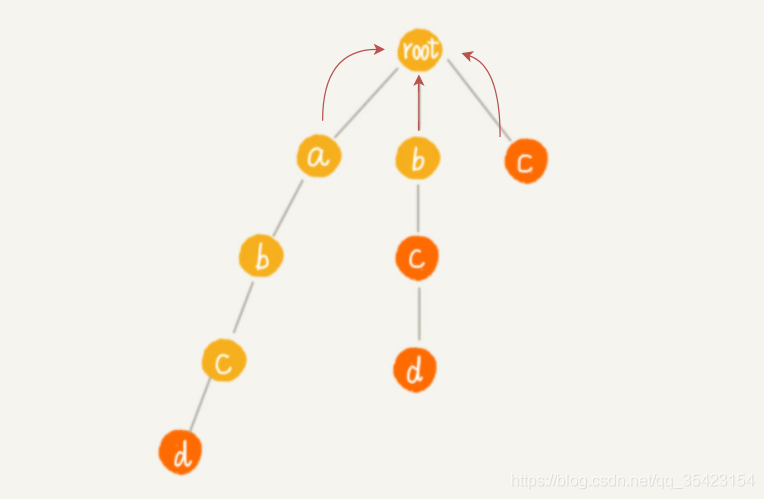
那麼如何求出子節點的失敗指標呢?為保證失敗指標指向的位置往上即為匹配的字尾,所以要使得字尾匹配,我們就需要到我們的失敗指標中尋找與子節點匹配的節點,如果找不到,則沿著失敗指標繼續往它的失敗指標繼續尋找,如果到了最頂上還沒有找到,則認為根節點為它的失敗指標。
總結一下
- 根節點的失敗指標為空
- 一個節點的失敗指標只能在它的上層
- 需要在父節點的失敗節點中找到與子節點匹配的節點,如果找不到則沿著失敗節點繼續向上,找它的失敗節點是否存在匹配節點,如果存在,則該節點就是子節點的失敗節點。
- 如果沒有上層沒有任何可匹配的節點,則失敗指標指向根節點
為了方便理解過程,我一層一層往下進行構建
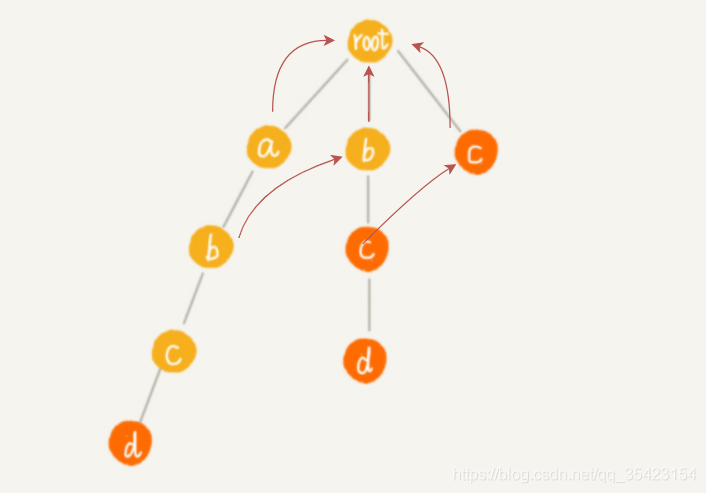
由於前往a的失敗節點root,可以找到匹配b的節點,所以將第二層的b作為子節點b的失敗指標,c同理
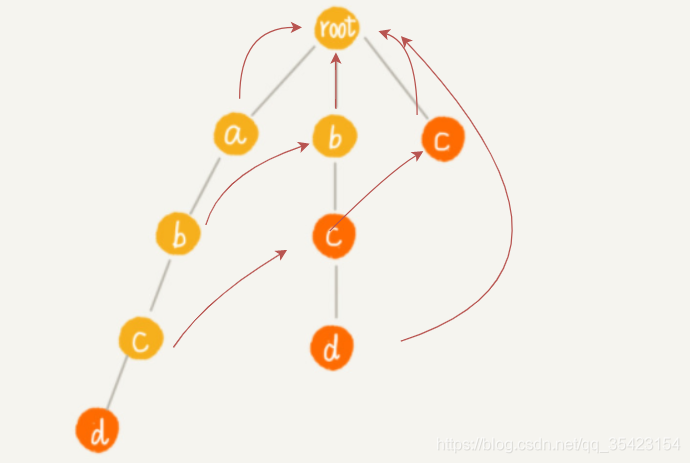
c與上層同理,這裡看d。由於d的父節點c的失敗指標c中並不存在匹配節點,所以向c的失敗指標繼續尋找,由於c的失敗指標為根節點,且也不存在匹配節點,此時已經到頭,所以d的失敗指標為根節點
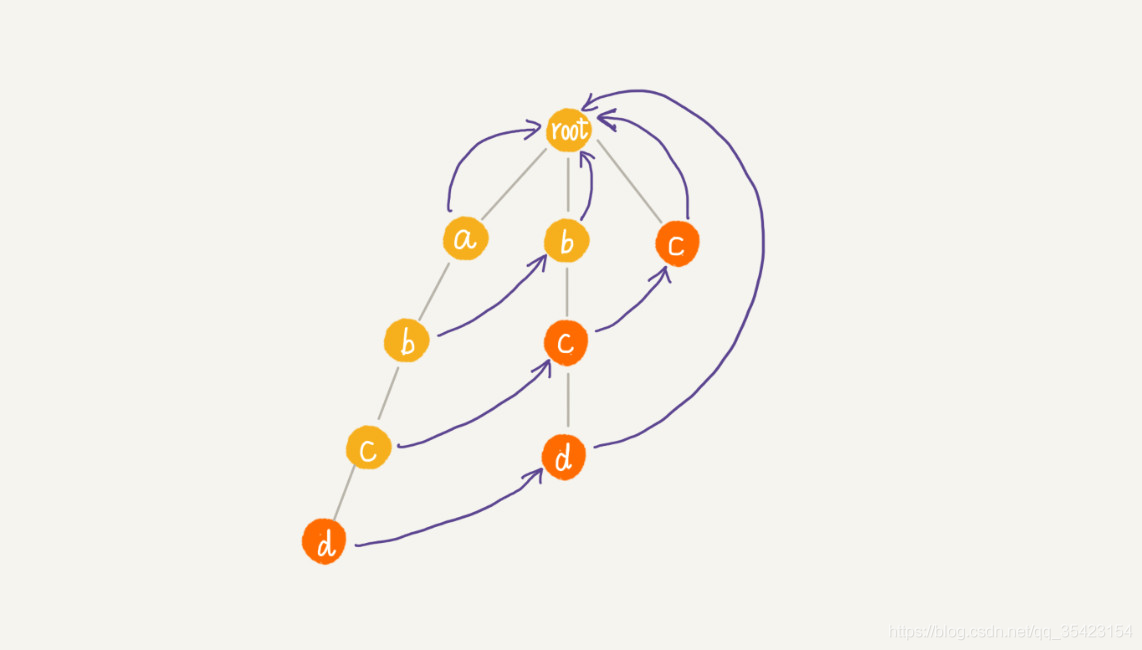
最終構建結果
程式碼如下,詳細思路都寫在註釋中
//構建失敗指標
void AC::buildFailurePointer()
{
//藉助佇列來完成層序遍歷
queue<ACNode*> q;
q.push(_root);
while (!q.empty())
{
ACNode* parent = q.front();
q.pop();
//遍歷所有孩子節點
for (auto& sub : parent->_subNode)
{
//如果父節點節點為根節點,則將孩子節點的失效指標全部設定為根節點
if (parent == _root)
{
sub.second->_fail = _root;
}
else
{
ACNode* failParent = parent->_fail; //父節點的失敗指標
while (failParent != nullptr)
{
auto failChild = failParent->_subNode.find(sub.second->_data); //尋找失敗指標中是否存在一個子節點能與我們的子節點匹配
if (failChild != failParent->_subNode.end()) //如果存在,則這個子節點就是我們子節點的失敗指標
{
sub.second->_fail = failChild->second;
break;
}
//如果找不到,則繼續向上,尋找失敗指標的失敗指標是否有這麼一個節點
failParent = failParent->_fail;
}
//如果一直找到最頂上也找不到,則將失敗指標設定為根節點
if (failParent == nullptr)
{
sub.second->_fail = _root;
}
}
//將子節點加入佇列中
q.push(sub.second);
}
}
}
匹配
講了那麼多原理,接下來就直接看看AC自動機是如何完成匹配的,此時主串為abcd,模式串為abcd,bc,bcd,c。
匹配主要包含以下兩種規則
- 匹配成功時,如果當前並不是一個完整的模式串,則繼續往下進行匹配。如果是一個完整的模式串,此節點匹配完成。但是匹配完成並不意味著中斷,此時我們還要利用失敗指標繼續去匹配下一個查詢詞,所以直到我們的結果指標回到根節點之前,都會一直通過失敗指標查詢匹配的模式串
- 如果匹配失敗,則前往失敗指標中繼續匹配,不斷重複這一過程
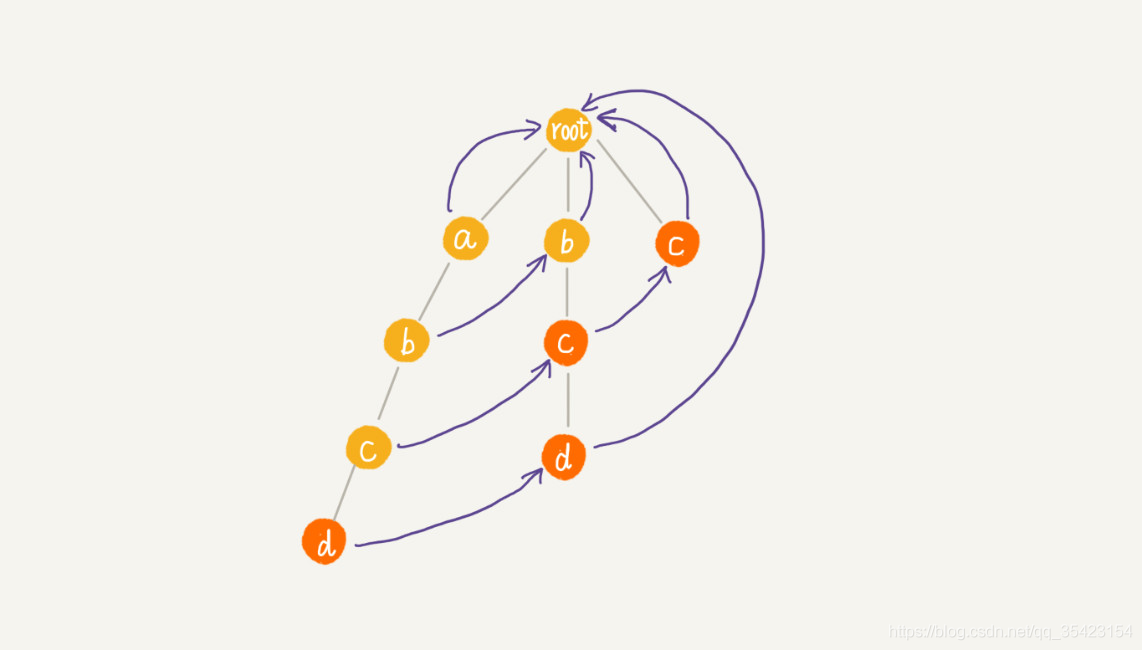
簡單描述上圖的查詢流程
- 第一輪查詢a,進入最左邊的模式串,此時不夠成單詞,失敗指標指向root,查詢不到
- 第二輪查詢b,ab不構成單詞,進入失敗指標b,b也不構成單詞
- 第三輪查詢c,abc不構成單詞,進入失敗指標c,此時bc匹配成功。接著進入失敗指標c,此時c也匹配成功。
- 第四輪查詢,abcd構成單詞,查詢成功,接著進入失敗指標d,bcd也成功匹配。
所以結果cd,abcd,bcd,c全部匹配成功
AC自動機的演演算法流程十分複雜,文字很難描述,所以我直接給出程式碼,並在其中寫明瞭註釋,如果還是搞不懂的可以一步一步進行偵錯。
//匹配模式串
void AC::match(const string& str) const
{
if (str.empty())
{
return;
}
ACNode* parent = _root;
for (int i = 0; i < str.size(); i++)
{
ACNode* sub = parent->_subNode[str[i]];
//如果子節點中找不到,則前往失敗指標中尋找
while (sub == nullptr && parent != _root)
{
parent = parent->_fail;
}
sub = parent->_subNode[str[i]];
//如果還是找不到,則說明已經沒有任何匹配的了,直接回到根節點
if (sub == nullptr)
{
parent = _root;
}
else
{
parent = sub; //繼續查詢下一個字元
}
ACNode* result = parent;
while (result != _root)
{
//如果當前構成一個單詞
if (result->_isEnd == true)
{
//輸出匹配的模式串
cout << str.substr(i - result->_length + 1, result->_length) << endl;
}
result = result->_fail; //如果無法構成一個單詞,則繼續前往失敗指標中繼續尋找
}
}
}
完整程式碼
除了匹配和失敗指標的構建,其他步驟都和Trie樹一樣,所以可以直接複用之前的程式碼。
需要注意的是,每次插入和刪除之後都必須重新構建失敗指標
#include<unordered_map>
#include<string>
#include<vector>
#include<queue>
#include<iostream>
using namespace std;
namespace lee
{
struct ACNode
{
ACNode(char data = '\0')
: _data(data)
, _isEnd(false)
, _length(-1)
, _fail(nullptr)
{}
char _data; //當前字元
bool _isEnd; //標記當前是否能構成一個單詞
int _length; //當前模式串長度
ACNode* _fail; //失敗指標
unordered_map<char, ACNode*> _subNode; //子節點
};
class AC
{
public:
AC()
: _root(new ACNode())
{}
~AC()
{
delete _root;
}
//防拷貝
AC(const AC&) = delete;
AC& operator=(const AC&) = delete;
void buildFailurePointer(); //構建失敗指標
void match(const string& str) const; //匹配模式串
void insert(const string& str); //插入字串
private:
ACNode* _root; //根節點
};
//插入字串
void AC::insert(const string& str)
{
if (str.empty())
{
return;
}
ACNode* cur = _root;
for (size_t i = 0; i < str.size(); i++)
{
//如果找不到該字元,則在對應層中插入
if (cur->_subNode.find(str[i]) == cur->_subNode.end())
{
cur->_subNode.insert(make_pair(str[i], new ACNode(str[i])));
}
cur = cur->_subNode[str[i]];
}
cur->_isEnd = true; //標記該單詞存在
cur->_length = str.size(); //標記該單詞長度
}
//構建失敗指標
void AC::buildFailurePointer()
{
//藉助佇列來完成層序遍歷
queue<ACNode*> q;
q.push(_root);
while (!q.empty())
{
ACNode* parent = q.front();
q.pop();
//遍歷所有孩子節點
for (auto& sub : parent->_subNode)
{
//如果父節點節點為根節點,則將孩子節點的失效指標全部設定為根節點
if (parent == _root)
{
sub.second->_fail = _root;
}
else
{
ACNode* failParent = parent->_fail; //父節點的失敗指標
while (failParent != nullptr)
{
auto failChild = failParent->_subNode.find(sub.second->_data); //尋找失敗指標中是否存在一個子節點能與我們的子節點匹配
if (failChild != failParent->_subNode.end()) //如果存在,則這個子節點就是我們子節點的失敗指標
{
sub.second->_fail = failChild->second;
break;
}
//如果找不到,則繼續向上,尋找失敗指標的失敗指標是否有這麼一個節點
failParent = failParent->_fail;
}
//如果一直找到最頂上也找不到,則將失敗指標設定為根節點
if (failParent == nullptr)
{
sub.second->_fail = _root;
}
}
//將子節點加入佇列中
q.push(sub.second);
}
}
}
//匹配模式串
void AC::match(const string& str) const
{
if (str.empty())
{
return;
}
ACNode* parent = _root;
for (int i = 0; i < str.size(); i++)
{
ACNode* sub = parent->_subNode[str[i]];
//如果子節點中找不到,則前往失敗指標中尋找
while (sub == nullptr && parent != _root)
{
parent = parent->_fail;
}
sub = parent->_subNode[str[i]];
//如果還是找不到,則說明已經沒有任何匹配的了,直接回到根節點
if (sub == nullptr)
{
parent = _root;
}
else
{
parent = sub; //繼續查詢下一個字元
}
ACNode* result = parent;
while (result != _root)
{
//如果當前構成一個單詞
if (result->_isEnd == true)
{
//輸出匹配的模式串
cout << str.substr(i - result->_length + 1, result->_length) << endl;
}
result = result->_fail; //如果無法構成一個單詞,則繼續前往失敗指標中繼續尋找
}
}
}
};
這裡我給出幾個敏感詞進行測試,檢視是否能夠全部匹配出來
int main()
{
lee::AC ac;
ac.insert("ass");
ac.insert("fuck");
ac.insert("shit");
ac.insert("cao");
ac.insert("sb");
ac.insert("nmsl");
ac.insert("dead");
ac.buildFailurePointer();
ac.match("fuckyou,nmslsb");
return 0;
}
匹配成功,這裡的匹配功能其實就已經是敏感詞過濾的一個原型程式碼了,我們只需要將匹配到的詞替換成遮蔽符號*即可,為了方便演示所以我才改成輸出模式串
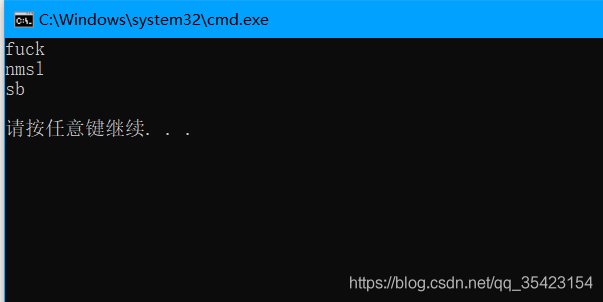
效能計算
AC自動機的構建包含兩個步驟,Trie樹的構建以及失敗指標的構建。
Trie樹構建的時間複雜度
假設模式串平均長度為M,個數為Z,則構建Trie樹的時間複雜度為O(M * Z)
失敗指標構建的時間複雜度
假設Trie樹中總節點數為K,模式串平均長度為M
失敗指標構建的時間複雜度為O(M * K)
匹配的時間複雜度
匹配需要遍歷主串,所以這一部分的時間複雜度為O(N),N為主串長度。
我們需要去匹配各個模式串,假設模式串平均長度為M,則匹配的時間複雜度為O(N * M)。
並且由於敏感詞一般不會很長,所以在實際情況下,這個時間複雜度可以近似於O(N)
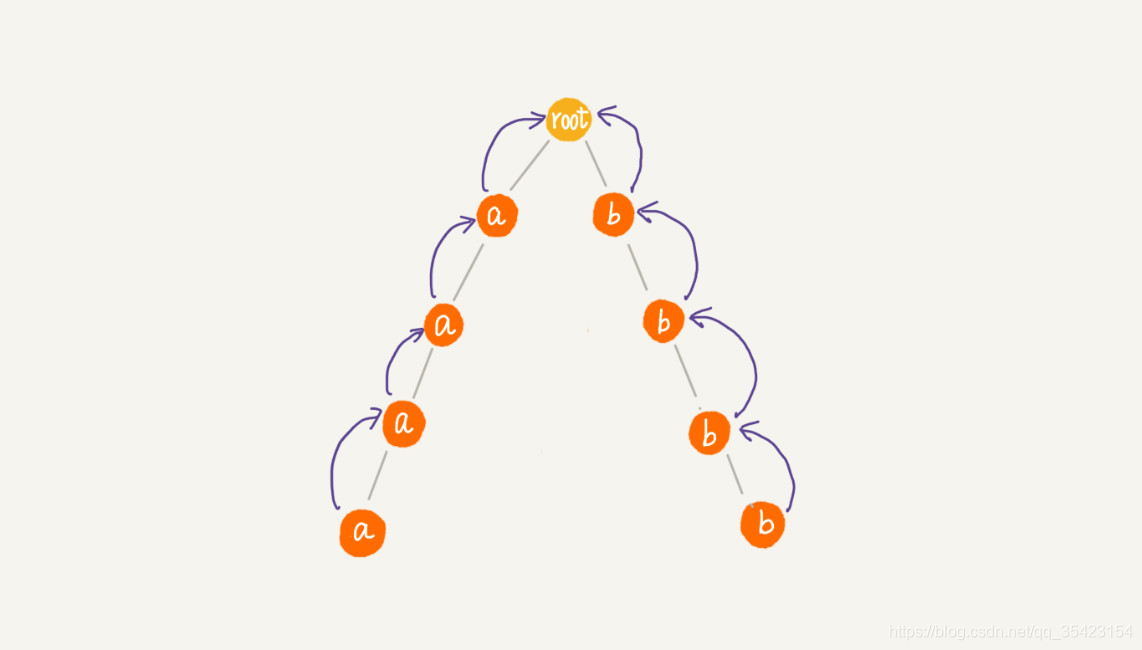
但是在下圖這種大部分的失效指標都指向根節點時,AC自動機的效能會退化的跟Trie樹一樣、