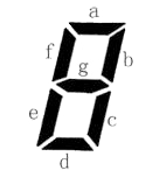試題 A: 門牌製作本題總分：5 分

【問題描述】
小藍要為一條街的住戶製作門牌號。這條街一共有 2020 位住戶，門牌號從 1 到 2020 編號。小藍製作門牌的方法是先製作 0 到 9 這幾個數位字元，最後根據需要將字符貼上到門牌上，例如門牌 1017 需要依次貼上字元 1、0、1、7，即需要 1 個字元 0，2 個字元 1，1 個字元 7。請問要製作所有的 1 到 2020 號門牌，總共需要多少個字元 2？
【答案提交】
這是一道結果填空的題，你只需要算出結果後提交即可。本題的結果為一個整數，在提交答案時只填寫這個整數，填寫多餘的內容將無法得分。

題解

直接手推，100以內個位數有10個2，十位數有10個2，所以100以內共有20個2；1000以內有10個100，所以有1020=200個2，在百位上有100個2，所以1000以內共有300個2；2000以內有2個1000，所以有2300個2，共有600個2；2020以內有21個千位的2以及1個十位的2和2個個位上的2，共24個2；綜上，一共有624個2。

程式碼

略

試題 B: 既約分數本題總分：5 分

【問題描述】
如果一個分數的分子和分母的最大公約數是 1，這個分數稱為既約分數。例如， $\frac{3 }{4}, \frac{5} {2}, \frac{1}{ 8}, \frac{7}{ 1}$ 都是既約分數。請問，有多少個既約分數，分子和分母都是 1 到 2020 之間的整數（包括 1 和 2020）？
【答案提交】
這是一道結果填空題，你只需要算出結果後提交即可。本題的結果為一個整數，在提交答案時只填寫這個整數，填寫多餘的內容將無法得分。

題解

資料不大，直接列舉並求GCD統計合法的方案即可。

答案：2481215

程式碼

#include <bits/stdc++.h>

using namespace std;

int gcd(int a, int b) {
	if (b == 0) return a;
	return gcd(b, a%b);
}

int main() {
	int ans = 0;
	for (int i = 1; i <= 2020; i++) {
		for (int j = 1; j <= 2020; j++) {
			if (gcd(i, j) == 1) {
				ans ++;
			}
		}
	}
  printf("%d\n", ans);
  return 0;
}

試題 C: 蛇形填數本題總分：10 分

【問題描述】
如下圖所示，小明用從 1 開始的正整數「蛇形」填充無限大的矩陣。

容易看出矩陣第二行第二列中的數是 5。請你計算矩陣中第 20 行第 20 列的數是多少？
【答案提交】
這是一道結果填空的題，你只需要算出結果後提交即可。本題的結果為一個整數，在提交答案時只填寫這個整數，填寫多餘的內容將無法得分。

題解

直接模擬，可以利用每條直線內的點截距相同，相鄰的直線截距差1的特徵進行模擬；

找規律會快點，對於處在對角線的點所在的左上三角的邊長為 $2 (n - 1) + 1$ ，即 $2 n - 1$ 。我們把這個上三角的規模為 $Sn=\frac{t(t+1)}{2}$ ，其中， $t = 2 n - 1$ 。我們計算前 $t - 1$ 層的規模，然後加上第 $t$ 層的規模的一半上取整即可，上取整的原因是對角線層一定為奇數。
$s1=\frac{38*(38+1)}{2}=741，s2=\lceil \frac{39}{2} \rceil=20，ans=s1+s2=761$

答案：761

程式碼

略

試題 D: 跑步鍛鍊本題總分：10 分

【問題描述】
小藍每天都鍛鍊身體。正常情況下，小藍每天跑 1 千米。如果某天是週一或者月初（1 日），為了激勵自己，小藍要跑 2 千米。如果同時是週一或月初，小藍也是跑 2 千米。小藍跑步已經堅持了很長時間，從 2000 年 1 月 1 日週六（含）到 2020 年 10 月 1 日週四（含）。請問這段時間小藍總共跑步多少千米？
【答案提交】
這是一道結果填空的題，你只需要算出結果後提交即可。本題的結果為一個整數，在提交答案時只填寫這個整數，填寫多餘的內容將無法得分。

題解

模擬即可，注意閏年的情況。

答案：8879

程式碼

#include <bits/stdc++.h>

using namespace std;

int month[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int main() {
  int y = 2000, m = 1, d = 1, w = 6, ans = 0;
  while(true) {
    ans += (d == 1 || w == 1) + 1;
    if (y == 2020 && m == 10 && d == 1) {
			break;
		}
    w = (w + 1) % 7;
    d = d + 1;
    if((y % 400 == 0 || y % 4 == 0 && y % 100 != 0) && m == 2) {
    	if (d > month[m] + 1) {
				d = 1;
				m += 1;
			}
    } else if (d > month[m]) {
			d = 1;
      m += 1;
		}
    if(m == 13) {
      y += 1;
      m = 1;
    }
  }
  printf("%d\n", ans);
	return 0;
}

試題 E: 七段碼本題總分：15 分

【問題描述】
小藍要用七段碼數碼管來表示一種特殊的文字。

上圖給出了七段碼數碼管的一個圖示，數碼管中一共有 7 段可以發光的二極管，分別標記為 a, b, c, d, e, f, g。小藍要選擇一部分二極體（至少要有一個）發光來表達字元。在設計字元的表達時，要求所有發光的二極體是連成一片的。例如：b 發光，其他二極體不發光可以用來表達一種字元。例如：c 發光，其他二極體不發光可以用來表達一種字元。這種方案與上一行的方案可以用來表示不同的字元，儘管看上去比較相似。例如：a, b, c, d, e 發光，f, g 不發光可以用來表達一種字元。例如：b, f 發光，其他二極體不發光則不能用來表達一種字元，因為發光的二極體沒有連成一片。
請問，小藍可以用七段碼數碼管表達多少種不同的字元？
【答案提交】
這是一道結果填空的題，你只需要算出結果後提交即可。本題的結果為一個整數，在提交答案時只填寫這個整數，填寫多餘的內容將無法得分。

題解

列舉子集，一共有 $2^7$ 種方案。當方案中聯通塊大於等於2時，非法。判斷聯通塊可以用並查集或者dfs。建圖的時候可以根據 7 管碼的鄰接情況建鄰接矩陣或鄰接表。

答案：80

程式碼

#include <bits/stdc++.h>

using namespace std;

int G[8][8], vis[8];
int pack[8], sz;
int ans;

void init() {
	G[1][2] = 1; G[1][6] = 1;
	G[2][3] = 1; G[2][7] = 1;
	G[3][4] = 1; G[3][7] = 1;
	G[4][5] = 1;
	G[5][6] = 1; G[5][7] = 1;
	G[6][7] = 1;

	for (int i = 1; i <= 7; i++) {
		for (int j = 1; j <= i; j++) {
			G[i][j] = G[j][i];
		}
	}
}

void dfs1(int u) {
	vis[u] = 0;
	for (int i = 1; i <= 7; i++) {
		if (i != u && G[u][i] == 1 && vis[i] == 1) {
			dfs1(i);
		}
	}
}

void dfs2(int index) { //列舉子集
	if (index == 8) {
		if (sz > 0) {
			dfs1(pack[1]); //處理連通塊
			int flag = 1;
			for (int i = 1; i <= sz; i++) {
				if (vis[pack[i]] == 1) {
					flag = 0;
				} else {
					vis[pack[i]] = 1; //還原
				}
			}
			if (flag == 1) {
				ans ++;
			}
		}
		return ;
	}
	vis[index] = 1;
	pack[++sz] = index;
	dfs2(index + 1);
	vis[index] = 0;
	--sz;
 	dfs2(index + 1);
	return ;
}

int main() {
	init();
	dfs2(1);
	printf("%d\n", ans);
	return 0;
}

試題 F: 成績統計時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：15 分

【問題描述】
小藍給學生們組織了一場考試，卷面總分為 100 分，每個學生的得分都是一個 0 到 100 的整數。如果得分至少是 60 分，則稱為及格。如果得分至少為 85 分，則稱為優秀。
請計算及格率和優秀率，用百分數表示，百分號前的部分四捨五入保留整
數。
【輸入格式】
輸入的第一行包含一個整數 n，表示考試人數。接下來 n 行，每行包含一個 0 至 100 的整數，表示一個學生的得分。
【輸出格式】
輸出兩行，每行一個百分數，分別表示及格率和優秀率。百分號前的部分四捨五入保留整數。
【樣例輸入】
7
80
92
56
74
88
100
0
【樣例輸出】
71%
43%
【評測用例規模與約定】
對於 50% 的評測用例，1≤n≤100。對於所有評測用例，1≤n≤10000。

題解

簡單題，先統計及格和優秀的人數，再計算相應的比例，注意四捨五入以及百分比的條件。還有就是優秀一定及格。

程式碼

#include <bits/stdc++.h>

using namespace std;

int main() {
	int n, pass = 0, excellent = 0;
	int score;
	double ans1, ans2;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &score);
		if (score >= 85) {
			pass ++;
			excellent ++;
		} else if (score >= 60) {
			pass ++;
		}
	}
	ans1 = (100.0*pass/n+0.5);
	ans2 = (100.0*excellent/n+0.5);
	printf("%d%%\n%d%%\n", (int)ans1, (int)ans2);
	return 0;
}

試題 G: 迴文日期時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：20 分

【問題描述】
2020 年春節期間，有一個特殊的日期引起了大家的注意：2020 年 2 月 2 日。因為如果將這個日期按「yyyymmdd」的格式寫成一個 8 位數是 20200202，恰好是一個迴文數。我們稱這樣的日期是迴文日期。有人表示 20200202 是「千年一遇」的特殊日子。對此小明很不認同，因為不到 2 年之後就是下一個迴文日期：20211202 即 2021 年 12 月 2 日。也有人表示 20200202 並不僅僅是一個迴文日期，還是一個 ABABBABA 型的迴文日期。對此小明也不認同，因為大約 100 年後就能遇到下一個 ABABBABA 型的迴文日期：21211212 即 2121 年 12 月 12 日。算不上「千年一遇」，頂多算「千年兩遇」。給定一個 8 位數的日期，請你計算該日期之後下一個迴文日期和下一個 ABABBABA 型的迴文日期各是哪一天。
【輸入格式】
輸入包含一個八位整數 N，表示日期。
【輸出格式】
輸出兩行，每行 1 個八位數。第一行表示下一個迴文日期，第二行表示下一個 ABABBABA 型的迴文日期。
【樣例輸入】
20200202
【樣例輸出】
20211202
21211212
【評測用例規模與約定】
對於所有評測用例，10000101 ≤ N ≤ 89991231，保證 N 是一個合法日期的 8 位數表示。

題解

兩種思路，第一種，直接模擬日期遞增，然後再判斷該日期是否為迴文串，找到最近日期即可。直觀地感覺日期地規模為 $8*10^7$ ，但題目有提示規模在一千以內，所以放心模擬即可。

這裡主要講第二種，由於題目輸出提示，我們可以得到年份一定為四位數，所以把所有可能的年份列舉處理，規模是 $10^4$ 。年份一出來，日期就已固定，然後把非法日期篩掉。最後去找最近的日期即可。注意，這裡迴文的型別有兩種，分別存到不同的表中即可，當然『ABABBABA』型是迴文的子集。

這裡似乎有個坑點，當 n 是最後一個 8 位的 ABABBABA 日期或者最後一個迴文日期怎麼辦？不要怕，注意：10000101 ≤ N ≤ 89991231，所以兩個答案均有解。

程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = (int)1e4+5;

int month[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

struct node {
	int y, m, d;
	bool operator < (const node& B) const{
		if (y == B.y) {
			if (m == B.m) return d < B.d;
			return m < B.m;
		}
		return y < B.y;
	}
	
	bool operator == (const node& B) const{
		return y == B.y && m == B.m && d == B.d;
	}
	
}tab1[N], tab2[N];

int n1, n2; //合法迴文日期和ABABBABA迴文的規模

//判斷日期是否合法
bool judge(node& d) {
  if (d.m < 1 || d.m > 12) return false;
	int mlimit = month[d.m];
	if (d.m == 2 && (d.y % 400 == 0 || d.y % 4 ==0 && d.y % 100 != 0)) mlimit ++; //閏年
	if (d.d < 1 || d.d > mlimit) return false;
  return true;
}

int main() {
	int idx;
	char str[8];
	node in, cur;
	scanf("%s", str);
	in.y = (str[0]-'0')*1000+(str[1]-'0')*100+(str[2]-'0')*10+(str[3]-'0');
	in.m = (str[4]-'0')*10+(str[5]-'0');
	in.d = (str[6]-'0')*10+(str[7]-'0');
	n1 = n2 = 0;
	
	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 10; j++) {
			cur.y = i*1000+j*100+i*10+j;
			cur.m = cur.d = j*10+i;
			if (judge(cur)) tab2[n2++] = cur;
			for (int z = 0; z < 10; z++) {
				for (int k = 0; k < 10; k++) {
					cur.y = i*1000+j*100+z*10+k;
					cur.m = k*10+z; cur.d = j*10+i;
					if (judge(cur)) tab1[n1++] = cur;
				}
			}
		}
	}
	
	sort(tab1, tab1+n1);
	sort(tab2, tab2+n2);
	
	for (int i = 0; i < n1; i++) {
		if (tab1[i] == in) {
			printf("%d%d%d%d%d%d%d%d\n",
				tab1[i+1].y/1000,
				tab1[i+1].y/100 % 10,
				tab1[i+1].y/10 % 10,
				tab1[i+1].y % 10,
				tab1[i+1].m/10,
				tab1[i+1].m % 10,
				tab1[i+1].d/10,
				tab1[i+1].d % 10);
			break;
		}
	}
	for (int i = 0; i < n2; i++) {
		if (tab2[i] == in) {
			printf("%d%d%d%d%d%d%d%d\n",
				tab2[i+1].y/1000,
				tab2[i+1].y/100 % 10,
				tab2[i+1].y/10 % 10,
				tab2[i+1].y % 10,
				tab2[i+1].m/10,
				tab2[i+1].m % 10,
				tab2[i+1].d/10,
				tab2[i+1].d % 10);
			break;
		}
	}
	return 0;
}

試題 H: 子串分值和時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：20 分

【問題描述】
對於一個字串 S，我們定義 S 的分值 f(S) 為 S 中出現的不同的字元個數。例如 f(」aba」) = 2，f(」abc」) = 3, f(」aaa」) = 1。現在給定一個字串 S[0…n−1]（長度為 n），請你計算對於所有 S 的非空子串 S[i…j](0≤i≤ j < n)，f(S[i…j]) 的和是多少。
【輸入格式】
輸入一行包含一個由小寫字母組成的字串 S。
【輸出格式】
輸出一個整數表示答案。
【樣例輸入】
ababc
【樣例輸出】
28
【評測用例規模與約定】
對於 20% 的評測用例，1≤n≤10；對於 40% 的評測用例，1≤n≤100；對於 50% 的評測用例，1≤n≤1000；對於 60% 的評測用例，1≤n≤10000；對於所有評測用例，1≤n≤100000。

【樣例說明】

子串	f值
a	1
ab	2
aba	2
abab	2
ababc	3
b	1
ba	2
bab	2
babc	3
a	1
ab	2
abc	3
b	1
bc	2
c	1

題解

求 $\frac{n(n+1)}{2}$ 個非空子區間的區間種類數之和，直接列舉區間端點後計算區間種類數複雜度會比較高。我們換種思路，直接計算每個點對於它存在區間的貢獻。對於一個區間多個相同的數位，其貢獻歸為第一個出現的數位或者最後一個出現的數位，如果是前者則要維護一個類似 序列自動機 中的索引陣列，用來得到當前數位字首中該數位只出現 1 次的區間長度，記為 prenum ；包括該字首區間任意字尾的串的種類就可以直接計算出來，這是個分步乘法，字尾串的長度為 n-idx+1，記為 sufnum。綜上，每個點的貢獻我們就可以 $O (1)$ 時間內計算出來，所以總的複雜度為 $O (n)$ 。如果維護字尾第一次出現的位置則同理。

極限大小計算：
$ans=\sum_{i=1}^{n}i*(n-i+1)=n*\sum_{i=1}^{n}i-\sum_{i=1}^{n}i^2+\sum_{i=1}^{n}i=\frac{n(n+1)(n+2)}{6}$

注意，根據這個算式我們可以得出答案量級在 $10^{15}$ ，所以用長整型儲存足夠。

程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = (int)1e5 + 5;

char str[N];

int next[26]; //前索引

int main() {
	int n;
	long long ans = 0;
  scanf("%s", str);
  n = strlen(str);
	memset(next, -1, sizeof next);
  for(int i = 0; i < n; i++) {
      ans += 1LL * (i - next[str[i] - 'a']) * (n - i);
      next[str[i] - 'a'] = i;
  }
  printf("%lld\n", ans);
  return 0;
}

拓展

多次查詢的區間種類數：經典區間計數問題，用兩次樹狀陣列或者主席樹就可以離線解決
因為一開始審題有誤，看出區間如果一種字母出現多於 1 次，則不造成貢獻。如果設問是這樣的話還要預處理一個字尾第一次出現該數位的位置，答案就是：
$ans=\sum_{i=1}^{n}(i-pre\_index(val(i)))*(suf\_index(val(i))-i+1)$

試題 I: 平面切分時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：25 分

【問題描述】
平面上有 N 條直線，其中第 i 條直線是 y = Ai ·x + Bi。請計算這些直線將平面分成了幾個部分。
【輸入格式】
第一行包含一個整數 N。以下 N 行，每行包含兩個整數 Ai,Bi。
【輸出格式】
一個整數代表答案。
【樣例輸入】
3
1 1
2 2
3 3
【樣例輸出】
6
【評測用例規模與約定】
對於 50% 的評測用例，1≤ N ≤4, −10≤ Ai,Bi ≤10。對於所有評測用例，1≤ N ≤1000, −100000≤ Ai,Bi ≤100000。

題解

觀察結果，我們發現這樣一個規律，每次新增一條新的直線進來，一定會多一個平面。如果與之前的直線產生一個新的交點，則又會多出一個平面出來，如果多兩個交點則多兩個平面，以此類推。故當新增一條直線則產生的新的平面數為：新增的交點數 + 1。這裡的 1 可以理解為和無限遠的一個邊界所圍成的。綜上，總的平面數就是依次新增多條線的交點變化情況。當然，我們需要預先做一個去重的操作，因為兩條重合的直線只能算一條。

對於新增的一條直線最多會產生當前的直線數 - 1 個交點，所以如果純暴力操作地話則時間複雜度為 $O(n^3)$ ，顯然會超時，我們可以對於交點的維護搞一個 set 集合優化。時間複雜度將為 $O(n^2logn)$ ，臨界情況則只會到達 $1 e 7$ 。

在判斷交點的時候，為了避免浮點數帶來的誤差，直接記分子和分母，但這樣判斷大小的時候可能會乘爆 int ，用 long long 存一下即可，根據交點範圍顯然不會乘爆 long long。

程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = (int)1e3 + 5;

struct line {
	int A, B;
	bool operator < (const line& V) const{
		if (A == V.A) {
			return B < V.B;
		}
		return A < V.A;
	}
	bool operator == (const line& V) {
		return A == V.A && B == V.B;
	}
}arr[N];

struct ver {
	//x = (B2-B1)/(A1-A2)
	//y = A1x+B1
	int B2, B1;
	int A1, A2;
	
	bool operator < (const ver& V) const{ //左下到右上
		if (1ll*(B2-B1)*(V.A1-V.A2)==1ll*(V.B2-V.B1)*(A1-A2)) { //x1==x2
			//y1 < y2
			if (1ll*(V.A1-V.A2)*(A1-A2) > 0ll)
				return 1ll*(A1*B2-A2*B1)*(V.A1-V.A2) < 1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2);
			else
				return 1ll*(A1*B2-A2*B1)*(V.A1-V.A2) > 1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2);
		} else {
			//x1<x2
			if (1ll*(V.A1-V.A2)*(A1-A2)>0ll)
				return 1ll*(B2-B1)*(V.A1-V.A2) < 1ll*(V.B2-V.B1)*(A1-A2);
			else
				return 1ll*(B2-B1)*(V.A1-V.A2) > 1ll*(V.B2-V.B1)*(A1-A2);
		}
	}
	/*
	bool operator == (const ver& V) {
		if (1ll*(B2-B1)*(V.A1-V.A2)==1ll*(V.B2-V.B1)*(A1-A2) &&
				1ll*(A1*B2-A2*B1)*(V.A1-V.A2)==1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2))
				return true;
		return false;
	}
	*/
};

int n, cn; //原始線的數目 去重線數的目
long long ans = 2;
set<ver> s;

int main() {
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d%d", &arr[i].A, &arr[i].B);
	}

	sort(arr, arr+n);

	cn = 1;
	for (int i = 1; i < n; i++) { //去重
		if (arr[cn - 1] == arr[i]) continue;
		if (cn != i) arr[cn] = arr[i];
		cn ++;
	}
	
	ver cur;
	for(int i = 1; i < cn; i++) {
		s.clear();
		for (int j = 0; j < i; j++) {
			if (arr[i].A == arr[j].A) continue; //平行
			cur.A1 = arr[i].A; cur.B1 = arr[i].B;
			cur.A2 = arr[j].A; cur.B2 = arr[j].B;
      		if (!s.count(cur)) s.insert(cur); //出現新的交點
		}
		ans += s.size() + 1;
	}
	
	printf("%lld\n", ans);
  return 0;
}

試題 J: 字串排序時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：25 分

【問題描述】
小藍最近學習了一些排序演演算法，其中氣泡排序讓他印象深刻。
在氣泡排序中，每次只能交換相鄰的兩個元素。
小藍髮現，如果對一個字串中的字元排序，只允許交換相鄰的兩個字元，則在所有可能的排序方案中，氣泡排序的總交換次數是最少的。例如，對於字串 lan 排序，只需要 1 次交換。對於字串 qiao 排序，總共需要 4 次交換。小藍的幸運數位是 V，他想找到一個只包含小寫英文字母的字串，對這個串中的字元進行氣泡排序，正好需要 V 次交換。請幫助小藍找一個這樣的字符串。如果可能找到多個，請告訴小藍最短的那個。如果最短的仍然有多個，請告訴小藍字典序最小的那個。請注意字串中可以包含相同的字元。
【輸入格式】
輸入一行包含一個整數 V，為小藍的幸運數位。
【輸出格式】
輸出一個字串，為所求的答案。
【樣例輸入】
4
【樣例輸出】
bbaa
【樣例輸入】
100
【樣例輸出】
jihgfeeddccbbaa
【評測用例規模與約定】
對於 30% 的評測用例，1≤V ≤20。對於 50% 的評測用例，1≤V ≤100。對於所有評測用例，1≤V ≤10000。

題解

由於限定的的合法字元只有 26 個字母，假設沒有這個約束可以直接按完全逆序排序使得長度最小，然後在消去部分逆序數。而對於這題，首先字母是可以重複的，並且在長度相同若要保證字典序更小顯然要讓較大的字母數量較少，此時只要讓較小的字母較多即可。

這裡可能會陷入一個可貪心的思維誤區：這也是我下面展示的一個假演演算法的例子：錯誤點在字典序最優是一個全域性的特性，區域性字典序最優不能保證全域性字典序最優，所以正解應該是搜尋+剪枝。

程式碼

假演演算法：

#include <bits/stdc++.h>

using namespace std;

const int N = (int)1e4+5;

int num[N];

int main() {
	int n, m;
	int _max, id, len, sum;
	scanf("%d", &n);
	
	sum = 0; len = 0;
	while (sum < n) {
		id = 1;
		for (int i = 2; i <= 26; i++) { //找到s最小的點, 如果存在多個取字典序更小的
      if (num[i] < num[id]) id = i;
		}
		sum = sum + len - num[id];
		len ++;
		num[id] ++;
	}
	
	m = sum - n; //注意更新逆序數差值
	for (int i = 1; i <= 26; i++) {
		if (num[i]) {
			_max = i;
		}
	}
	
	for (int i = _max; i >= 1; i--) {
		for (int j = 0; j < num[i]; j++) {
			printf("%c", 'a'+i-1);
		}
	}
	printf("\n");
	
	for (int i = 1; i <= m; i++) {
		/*
		//儘量消去最大的數位，並且逆序數變化得最少，如果變化量相同則選擇字典序較小的方案
		id = 0; sum = INT_MAX;
		for (int j = 1; j <= 26; j++) {
			if (m - i + num[_max] - num[j] >= 0) {
				if (sum > num[j] - num[_max] + 1) {
					sum = num[j] - num[_max] + 1;
					id = j;
				}
			}
		}
		if (id) {
			num[id] ++;
			num[_max] --;
			if (!num[_max]) _max--;
			i += sum - 1;
			printf("~%d\n", id);
			continue;
		}
		*/
		
		for (int j = _max; j >= 1; j--) {
			id = 0;
			while(num[++id]!= num[j]);
			if (id != j) {
				num[id] ++;
				num[j] --;
				break;
			}
		}

		if (!num[_max]) {
			_max--;
		}
	}
	
	for (int i = _max; i >= 1; i--) {
		for (int j = 0; j < num[i]; j++) {
			printf("%c", 'a'+i-1);
		}
	}
	printf("\n");
  return 0;
}

搜尋+剪枝

#include <bits/stdc++.h>

using namespace std;

const int N = (int)1e4+5;

int num[N], res[N];
int n, m, _max, len;

bool judge(int letter) {
	int i = 26, j = letter;
	while (!res[i]) i--;
	if (i == j) {
		while (i > 0 && j > 0) {
			if (res[i] != num[j]) {
				return res[i] > num[j];
			} else {
				i--; j--;
			}
		}
	}
	return i > j;
}

void dfs(int letter, int curlen, int cursum, int l) {
	if (cursum > n) return ;
	if (letter > _max) return ;
	if (curlen > len) return ;
	
	if (curlen == len && cursum != n) return ;
	if (letter == _max && cursum != n) return ;
	
	if (cursum == n) {
		if (curlen < len || judge(letter)) { //長度減小或字典序減小更新結果
			len = curlen;
			for (int i = 1; i <= 26; i++) {
				res[i] = num[i];
			}
		}
		return ;
	}

	for (int i = 1; i <= l; i++) {
		num[letter + 1] = i;
		dfs(letter + 1, curlen + i, cursum + i * curlen, i);
	}
	num[letter + 1] = 0;
}

int main() {
	
	scanf("%d", &n);

	m = 0; len = 0;
	while (m < n) {
		int id = 1;
		for (int i = 2; i <= 26; i++) { //找到s最小的點, 如果存在多個取字典序更小的
      if (res[i] < res[id]) id = i;
		}
		m += len - res[id];
		_max = max(_max, id);
		len ++; res[id] ++;
	}
	
	dfs(0, 0, 0, 10);
	
	for (int i = _max; i >= 1; i--) {
		for (int j = res[i]; j > 0; j--) {
			printf("%c", i-1+'a');
		}
	}
	printf("\n");

  return 0;
}

第十一屆藍橋杯大賽軟體類省賽第二場 C/C++ 大學 B 組

試題 A: 門牌製作 本題總分：5 分

題解

程式碼

試題 B: 既約分數 本題總分：5 分

題解

程式碼

試題 C: 蛇形填數 本題總分：10 分

題解

程式碼

試題 D: 跑步鍛鍊 本題總分：10 分

題解

程式碼

試題 E: 七段碼 本題總分：15 分

題解

程式碼

試題 F: 成績統計 時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：15 分

題解

程式碼

試題 G: 迴文日期 時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：20 分

題解

程式碼

試題 H: 子串分值和 時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：20 分

題解

程式碼

拓展

試題 I: 平面切分 時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：25 分

題解

程式碼

試題 J: 字串排序 時間限制: 1.0s 記憶體限制: 256.0MB 本題總分：25 分

題解

程式碼