2020CCPC(秦皇島) - Kingdom‘s Power(樹形dp+貪心)

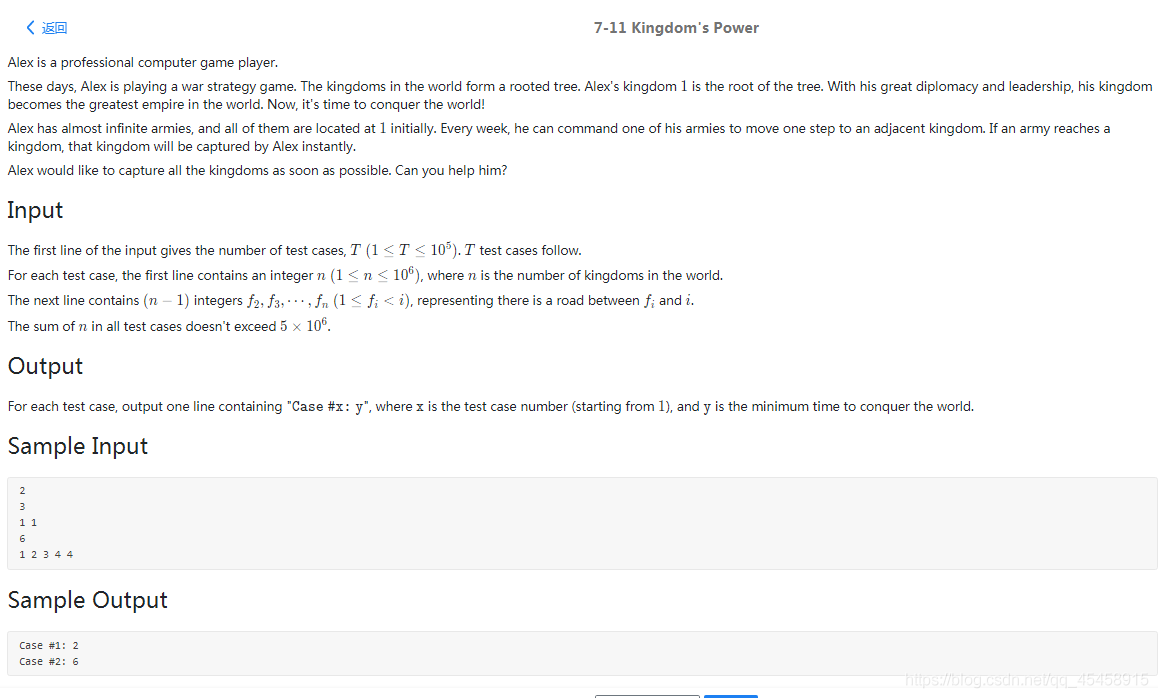
題目大意：給出一棵 n 個節點的有根樹，點 1 為根節點，現在在根節點有無窮多個士兵，每一秒可以控制任意一個士兵向任意一個單位移動一步，士兵移動到的點會被永久佔領，現在問最少需要經過多少秒，才能將所有的點都佔領

題目分析：首先不難看出的兩個小結論是：

如果所有的葉子節點都被佔領，那麼沿途的所有點也會被佔領，所以問題轉換為了到每個葉子節點的最短時間
第一步肯定是需要從根節點到其中一個葉子節點的，貪心去想，到深度最低的那個葉子節點一定是最優的

樹形dp維護一下從根節點過來更優還是從相鄰的葉子結點更優，然後更新答案即可，這裡參考了網上的解法，形式引數維護一個變數表示到達當前節點時的最短距離，遞迴的返回值是自底向上的最短距離，也就是從相鄰的葉子節點過來的距離，這個距離和深度取個最小值就是答案了

最後還有一點需要貪心去考慮，感覺這個就是本題的難點了，假設只有一個士兵，從根節點出發若想遍歷整棵樹的話，最短的路線一定是：對於每個子樹而言，最長的鏈只遍歷一次，其餘的鏈都會被遍歷兩次

基於此，對於每個子樹而言，我們只需要將其按照最長鏈進行排序即可，因為最後去遍歷的話一定只需要走一遍

程式碼：

//#pragma GCC optimize(2)
//#pragma GCC optimize("Ofast","inline","-ffast-math")
//#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<iostream>
#include<cstdio>
#include<string>
#include<ctime>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<stack>
#include<climits>
#include<queue>
#include<map>
#include<set>
#include<sstream>
#include<cassert>
#include<bitset>
#include<unordered_map>
using namespace std;
     
typedef long long LL;
     
typedef unsigned long long ull;
     
const int inf=0x3f3f3f3f;

const int N=1e6+100;

vector<pair<int,int>>node[N];

int deep[N],val[N];

int dfs1(int u,int dep)
{
	if(node[u].empty())
		return 1;
	deep[u]=dep;
	for(auto &it:node[u])
	{
		int v=it.second;
		it.first=max(it.first,dfs1(v,dep+1));
	}
	sort(node[u].begin(),node[u].end());
	return node[u].back().first+1;
}

int dfs2(int u,int dis)//返回值為自底向上的最短距離,dis儲存的是到達當前點的最短距離 
{
	val[u]=dis;
	if(node[u].empty())
		return 1;
	int mmin=dis;//到當前節點的最近距離 
	for(auto it:node[u])
	{
		int v=it.second;
		mmin=min(deep[u],dfs2(v,mmin+1));
	}
	return mmin+1;
}

int main()
{
#ifndef ONLINE_JUDGE
//  freopen("data.in.txt","r",stdin);
//  freopen("data.out.txt","w",stdout);
#endif
//  ios::sync_with_stdio(false);
	int w;
	cin>>w;
	int kase=0;
	while(w--)
	{
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			node[i].clear();
		for(int i=2;i<=n;i++)
		{
			int fa;
			scanf("%d",&fa);
			node[fa].push_back(make_pair(0,i));
		}
		dfs1(1,0);
		dfs2(1,0);
		LL ans=0;
		for(int i=1;i<=n;i++)
			if(node[i].empty())
				ans+=val[i];
		printf("Case #%d: %lld\n",++kase,ans);
	}



















    return 0;
}