Chapter02 演演算法分析

參考書本：
Data Structure and Algorithm Analysis in C

參考課程：
浙江大學-資料結構 陳越姥姥

幾個概念：
Def： T(N) <= cf(N) 記為 T(N) = O(f(N))
T(N) >= cf(N) 記為 T(N) = Ω(f(N))

在演演算法分析中，比較函數值的大小是沒有意義的，於是比較它們的相對增長率（relative rate of growth)

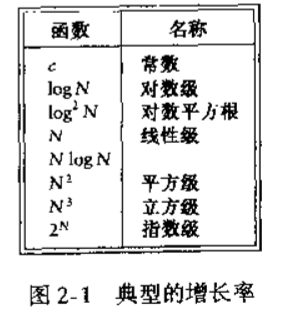
注意：
不要將低階項或常數放入大O。不要寫T(N) = O( 2N² ) 或 T(N) = O( N²+ N )， 這兩種的正確寫法都是T( N ) = O ( N² )。

法則：如果一個演演算法用的常數時間O( 1 )將問題的大小削減為其一部分（通常是1/2），那麼該演演算法就是O( logN )的。另一方面，如果只減少了一個常數（問題減少1）那麼這種演演算法就是O( N )的。

舉例：
對分查詢（binary search）

int BinarySearch(const int A[ ], int X, int N)
{
    int Low, Mid, High;

    Low = 0; High = N - 1;

    while (Low <= High )
    {
        Mid = ( Low + High ) / 2;
        if( A[Mid] < X )
            Low = Mid + 1;
        else if( A[Mid] > X)
            High = Mid - 1;
        else
            return Mid;     //Found
    }
    return -1;      //Not Found
}

int main()
{
    int A[10 + 5] = {0, 3, 5, 12, 23, 29, 47, 50, 72, 99};
    int X = 29;     //Target
    int N = 10;     //Number of numbers
	int index;
	
    index = BinarySearch(A, X, N);
	
	cout << index;	//Display 2	

    return 0;
}

只需要講mid與target去比較一次，就可以講問題縮短一半。因此，執行時間是O ( logN )。

歐幾里得演演算法
計算兩個整數的最大公因數（Gcd）

int Gcd(int M, int N)
{
    int Rem;

    while( N > 0 )
    {
        Rem = M % N;
        M = N;
        N = Rem;
    }
    return M;
}

int main()
{
    int M, N;
    int ans;

    M = 1989;
    N = 1590;

    ans = Gcd(M, N);

    cout << ans << endl;

    return 0;
}

由定理，如果M > N, 則 M mod N < M / 2，可知，一次M mod N的操作，使問題大小縮減一半，故執行時間是O( log N )