前言

前情提要：Lattice Planner從學習到放棄
盲目激情的移植apollo的lattice，體會到了痛苦，當時為了先儘快讓lattice演演算法在自己的框架裡跑起來，在摘用原始碼的時候做了很多欠考慮的改動，雖然快速實現了通過lattice planner規劃軌跡，然後達到循跡的效果，但是在隨後引入障礙物，產生了大量的坑，深深的被教育，也給帶頭大哥添了不少麻煩。

看懂流程==>理解原理 ==>成功實現

最終通過planner中的二次規劃實現了單車道內低速障礙物的避讓規劃。
簡明扼要：新增靜態障礙物→產生單車道內目標軌跡→繞行或停止

最近節奏比較撕裂，下午或晚上才能搞lattice的復現，但這個「重複造輪子」的過程真的獲益良多，和大哥們交流也多起來，知道好的輪子是什麼樣的，才能嘗試去改進或完善，一瓶不響半瓶咣噹，半瓶正是在下～保持積極與熱情，也期待大佬們各種指導....

一.靜態障礙物的引入

1.障礙物的格式

暫時不使用Apollo的那套，先用自有結構體接收障礙物資訊，然後壓入Obstacle類中即可。

對於靜態或低速障礙物，無非就是id、長寬高、位置以及朝向，動態障礙物暫時沒有進行。

2.自車sl的建立和障礙物的建立

自車相對於參考線起點裡程和橫向偏移量，以及障礙物的ST、SL資訊都是要計算的，對於動態障礙物，SL已經不足以滿足需求了吧？後續學習EM再拎出來分析。

二.單車道場景中面向靜態障礙物的避讓

1.軌跡規劃原理

軌跡=縱向軌跡+橫向軌跡，之前已經分析了縱向速度規劃的過程，以及橫縱向軌跡是如何combine成一條完整軌跡的。在lattice中，橫向軌跡生成有兩種方法：撒點取樣法、二次規劃法。

1.1基於取樣點的軌跡規劃

撒點法前邊也有記錄，知道了起始點和取樣點的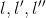 l,l{}',l{}'' ，然後求解對應的五次多項式的係數，便可得到對應的橫向軌跡，不重複了。

1.2基於二次規劃的軌跡規劃

Apollo原始碼中FLAGS_lateral_optimization預設是開啟的，即橫向規劃預設使用二次規劃進行，由於個人魯莽認為撒點會更直觀簡潔，所以關了這個標誌位，採用的是撒點取樣，隨後在實車偵錯時發現耗時很大，尤其是自車接近障礙物時，耗時飆升——軌跡數太多，障礙物碰撞檢測遍歷軌跡。額，設定比較低的工控機雪上加霜...然後試用一下二次規劃唄，wtf，超nice。

學習了程十三的軌跡規劃綜述。

Apollo中二次規劃求解使用的是OSQP求解器，官網：OSQP官網點這裡，二次規劃求解有很多方法，關於為何選取OSQP，速度快～為何這麼快，數學系的大佬們的戰場。標準的二次規劃形式：

下來要做的就很明確了：

搞清楚路徑規劃的約束；
搞清楚優化目標，即如何評價計算結果的優劣
轉換成osqp求解器需要的形式，呼叫求解器
坐等結果～

考慮車寬以及和障礙物的距離buffer，車輛的中心的橫向可移動範圍大概就是如下圖，Apollo中，前探60m，取樣點間隔1m，所以有60個取樣點，也可以根據實際情況調整。

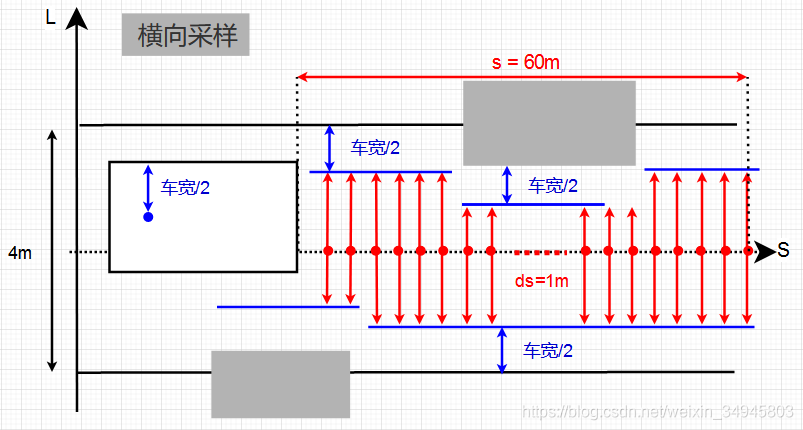
1.2.1 車輛橫向狀態量設計

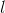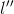橫向偏移量作為基本量，跑不掉，作為橫向速度變化率，當然也跑不掉； l{}'' 作為橫向加加速度，是控制乘坐舒適性的重要指標，也不能放掉；對於 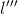l{}''' ，把軌跡看作可拉伸的彈力繩，三階導意味著其可拉伸的程度，可以用 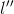l{}'' 差分計算。so，需要的量齊全了。狀態量可以得到：

$x=[l_{59}, l_{58} ,..., l_{0}, l_{59}', l_{58}' ,..., l_{0}', l_{59}'', l_{58}'' ,..., l_{0}'' ]^{T}$

1.2.2 車輛橫向軌跡約束的建立

整個約束建立主要考慮到：

1.自車不能與障礙物碰撞或駛出邊界，即 $l_{i}\in [l_{i_{left}} , l_{i_{right}}]$

2.軌跡應該保持連續，即相鄰兩個取樣點的 $l_{i+1}= l_{i}+{l_{i}}'\cdot \Delta s+\frac{1}{2}\cdot {{l_{i}}}''\cdot \Delta s^{2}+\frac{1}{6}\cdot {{l_{i}}}'''\cdot \Delta s^{3}$

3.軌跡應該保持光滑，即導數連續相鄰兩個取樣點的斜率 $l_{i+1}'=l_{i}'+l_{i}''\cdot \Delta s+\frac{1}{2}\cdot l_{i}'''\cdot \Delta s^{2}$

4.橫向加加速度(相對於s的二階偏導)應在一定範圍內，即 $\small l_{i}'''=\frac{\Delta l_{i}''}{\Delta s}=\frac{l_{i+1}''-l_{i}''}{\Delta s}\in [-0.1,0.1]$

公式2、3直接用的泰勒公式進行的2階和3階展開，將 $l_{i}'''=\frac{l_{i+1}''-l_{i}''}{\Delta s}$ 代入，可得到公式2和3的最終形式：

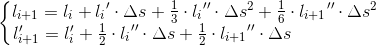
$\left\{\begin{matrix} l_{i+1}= l_{i}+{l_{i}}'\cdot \Delta s+\frac{1}{3}\cdot {{l_{i}}}''\cdot \Delta s^{2}+\frac{1}{6}\cdot {{l_{i+1}}}''\cdot \Delta s^{2} \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \\ l_{i+1}'= l_{i}'+\frac{1}{2}\cdot {l_{i}}''\cdot \Delta s+\frac{1}{2}\cdot {{l_{i+1}}}''\cdot \Delta s \end{matrix}\right.$

到這一步，基本上約束的內容已經很清晰了，整理後如下：

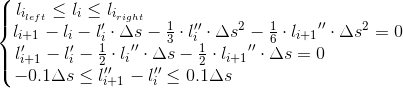
$\left\{\begin{matrix} l_{i_{left}}\leq l_{i}\leq l_{i_{right}} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \\ l_{i+1}- l_{i}-l_{i}'\cdot \Delta s-\frac{1}{3}\cdot l_{i}''\cdot \Delta s^{2}-\frac{1}{6}\cdot {{l_{i+1}}}''\cdot \Delta s^{2} =0 \\ l_{i+1}'- l_{i}'-\frac{1}{2}\cdot {l_{i}}''\cdot \Delta s-\frac{1}{2}\cdot {{l_{i+1}}}''\cdot \Delta s=0 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,\\ -0.1\Delta s\leq l_{i+1}''- l_{i}''\leq 0.1\Delta s \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \end{matrix}\right.$

即對於每一個取樣點，存在兩個不等式和兩個等式約束，一共60個取樣點，那麼約束至少應該為60x4=240個約束條件。

根據狀態量的形式，約束矩陣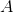也就定了（這裡不一定準確，若有不對求指導額..）：

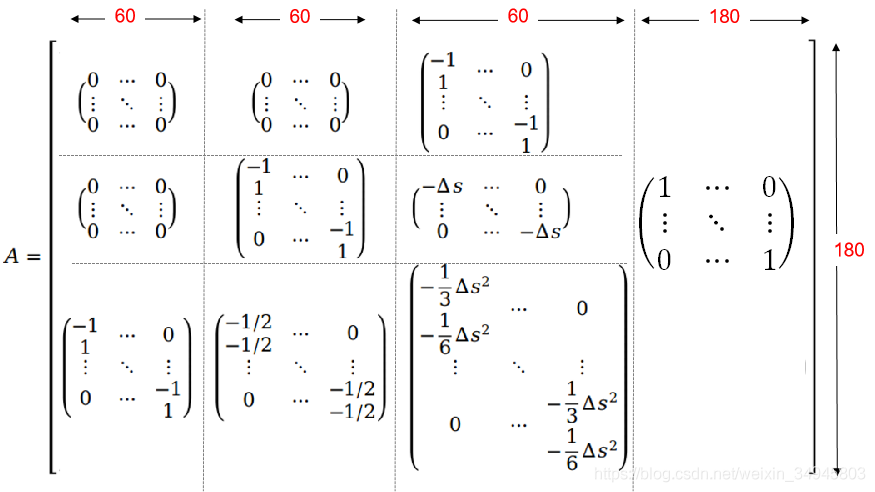
這裡使用的話貌似應該是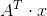 $A^{^{T}}\cdot x$ ，行列貌似反了...不管了，原理不變。

1.2.3 約束邊界的建立

前邊已經描述了約束的建立依據，根據障礙物對車道的侵佔情況，更新橫向位移 $l_{i}$ 的範圍，最終約束的上下邊界分別為：

$bound_{up}=[0.1, 0.1, ...,0.1,0,0,...,0,0,0,...,0,1.45,1.45,...,1.45,2,2,...,2]^{T}$

$bound_{low}=[-0.1, -0.1, ...,-0.1,0,0,...,0,0,0,...,0,-1.45,-1.45,...,-1.45,-2,-2,...,-2]^{T}$

其中-2,2作為預設值不充值，湊夠矩陣運算數量，最終用於：

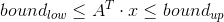
$bound_{low}\leq A^{T}\cdot x \leq bound_{up}$

1.2.3 目標函數的建立

二次規劃的目標為

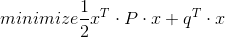
$minimize \frac{1}{2}x^{T}\cdot P\cdot x+q^{T}\cdot x$

其中，將權重作為P項對角陣傳入，左右邊界作為偏差項q用以控制軌跡和參考線的偏離程度，如下：

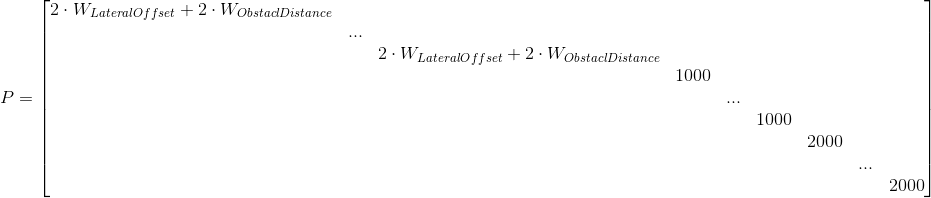
$P=\begin{bmatrix} 2\cdot W_{LateralOffset}+2\cdot W_{ObstaclDistance} & & & & & & & & \\ &... & & & & & & & \\ & &2\cdot W_{LateralOffset}+2\cdot W_{ObstaclDistance} & & & & & & \\ & & &1000 & & & & & \\ & & & &... & & & & \\ & & & & &1000 & & & \\ & & & & & &2000 & & \\ & & & & & & &... & \\ & & & & & & & &2000 \end{bmatrix}$

$q=[-2W_{LateralOffset}(l_-bound[0].first+l_-bound[0].second),...,-2W_{LateralOffset}(l_-bound[59].first+l_-bound[59].second)]$

至此，整個二次規劃建立所需要的材料，全部齊全。在二次規劃中，對於矩陣P，以目前形式來看一定是正定的額，是否意味著此問題是凸優化問題，且一定有可行解？求大佬指點。。。

1.2.5 約束矩陣的壓縮CSC

從上邊已經可以看到，建立起來的矩陣基本都非常稀疏，在運算過程中是非常不方便的，常見的稀疏矩陣壓縮方法主要有：

CSR—Compressed sparse row
CSC—Compressed sparse column

之前在學習apollo時，發現其採用的csc矩陣，當時並不瞭解，也是擴充套件後才知道，可見總結：csc_matrix稀疏矩陣理解至於為何選擇csc的原因可能是osqp官方使用的是csc？呼叫osqp建立workspace，需要以csc矩陣形式傳入求解器。

閒話一大堆，下面上程式碼。

2.Lattice planning二次規劃程式碼實現

lattice planner中通過呼叫Trajectory1dGenerator範例化後的成員函數，生成橫縱向軌跡，我們要看的常規撒點法和二次規劃都在其中，

// 5. generate 1d trajectory bundle for longitudinal and lateral respectively.
  Trajectory1dGenerator trajectory1d_generator(
      init_s, init_d, ptr_path_time_graph, ptr_prediction_querier);
  std::vector<std::shared_ptr<Curve1d>> lon_trajectory1d_bundle;
  std::vector<std::shared_ptr<Curve1d>> lat_trajectory1d_bundle;
  trajectory1d_generator.GenerateTrajectoryBundles(
      planning_target, &lon_trajectory1d_bundle, &lat_trajectory1d_bundle);

進入函數後，很清晰沒啥說的：縱向規劃+橫向規劃。

void Trajectory1dGenerator::GenerateTrajectoryBundles(
    const PlanningTarget& planning_target,
    Trajectory1DBundle* ptr_lon_trajectory_bundle,
    Trajectory1DBundle* ptr_lat_trajectory_bundle) {
  //縱向速度規劃
  GenerateLongitudinalTrajectoryBundle(planning_target,
                                       ptr_lon_trajectory_bundle);
  //橫向軌跡規劃
  GenerateLateralTrajectoryBundle(ptr_lat_trajectory_bundle);
}

在橫向規劃內，通過宏定義FLAGS_lateral_optimization，決定是否採用二次規劃，如下：

void Trajectory1dGenerator::GenerateLateralTrajectoryBundle(
    Trajectory1DBundle* ptr_lat_trajectory_bundle) const {
  //是否使用優化軌跡，true，採用五次多項式規劃
  if (!FLAGS_lateral_optimization) {
    auto end_conditions = end_condition_sampler_.SampleLatEndConditions();

    // Use the common function to generate trajectory bundles.
    GenerateTrajectory1DBundle<5>(init_lat_state_, end_conditions,
                                  ptr_lat_trajectory_bundle);
  } else {
    double s_min = init_lon_state_[0];
    double s_max = s_min + FLAGS_max_s_lateral_optimization;//FLAGS_max_s_lateral_optimization = 60

    double delta_s = FLAGS_default_delta_s_lateral_optimization;//規劃間隔為1m
    //橫向邊界
    auto lateral_bounds =
        ptr_path_time_graph_->GetLateralBounds(s_min, s_max, delta_s);

    // LateralTrajectoryOptimizer lateral_optimizer;
    std::unique_ptr<LateralQPOptimizer> lateral_optimizer(
        new LateralOSQPOptimizer);

    // 採用的是OSQP求解器
    lateral_optimizer->optimize(init_lat_state_, delta_s, lateral_bounds);

    auto lateral_trajectory = lateral_optimizer->GetOptimalTrajectory();

    ptr_lat_trajectory_bundle->push_back(
        std::make_shared<PiecewiseJerkTrajectory1d>(lateral_trajectory));
  }
}

流程很直白，通過GetLateralBounds函數獲取包含障礙物資訊的橫向邊界分佈，然後傳入lateral_optimizer->optimize()中開始osqp短暫愉快的一生，

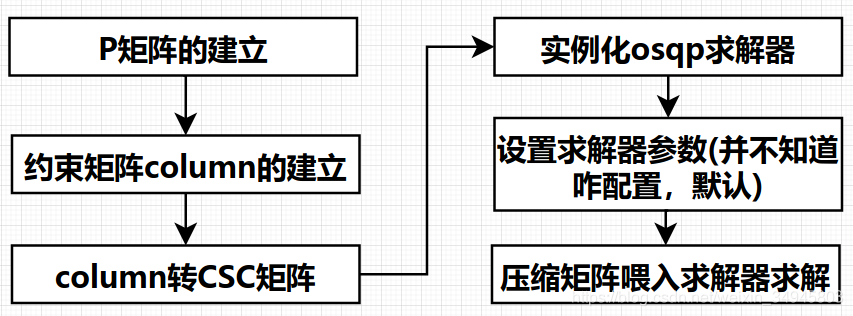
完整原始碼可看apollo：

bool LateralOSQPOptimizer::optimize(
    const std::array<double, 3>& d_state, const double delta_s,
    const std::vector<std::pair<double, double>>& d_bounds) {
  std::vector<c_float> P_data;
  std::vector<c_int> P_indices;
  std::vector<c_int> P_indptr;
  //建立目標函數中的P矩陣，主要包括權重分配
  CalculateKernel(d_bounds, &P_data, &P_indices, &P_indptr);
  delta_s_ = delta_s; //1m
  const int num_var = static_cast<int>(d_bounds.size());
  const int kNumParam = 3 * static_cast<int>(d_bounds.size());
  const int kNumConstraint = kNumParam + 3 * (num_var - 1) + 3; 
  c_float lower_bounds[kNumConstraint];
  c_float upper_bounds[kNumConstraint];

  const int prime_offset = num_var;
  const int pprime_offset = 2 * num_var;//=6？

  std::vector<std::vector<std::pair<c_int, c_float>>> columns;
  columns.resize(kNumParam);

  int constraint_index = 0;

  //constraint_index:0~2
  // d_i+1'' - d_i''
  for (int i = 0; i + 1 < num_var; ++i) {
    columns[pprime_offset + i].emplace_back(constraint_index, -1.0);
    columns[pprime_offset + i + 1].emplace_back(constraint_index, 1.0);
    //FLAGS_lateral_third_order_derivative_max=0.1
    lower_bounds[constraint_index] =
        -FLAGS_lateral_third_order_derivative_max * delta_s_;
    upper_bounds[constraint_index] =
        FLAGS_lateral_third_order_derivative_max * delta_s_;
    ++constraint_index;
  }

  //constraint_index:3~5
  // d_i+1' - d_i' - 0.5 * ds * (d_i'' + d_i+1'')
  for (int i = 0; i + 1 < num_var; ++i) {
    columns[prime_offset + i].emplace_back(constraint_index, -1.0);
    columns[prime_offset + i + 1].emplace_back(constraint_index, 1.0);
    columns[pprime_offset + i].emplace_back(constraint_index, -0.5 * delta_s_);
    columns[pprime_offset + i + 1].emplace_back(constraint_index,
                                                -0.5 * delta_s_);

    lower_bounds[constraint_index] = 0.0;
    upper_bounds[constraint_index] = 0.0;
    ++constraint_index;
  }

  //constraint_index:6~8
  // d_i+1 - d_i - d_i' * ds - 1/3 * d_i'' * ds^2 - 1/6 * d_i+1'' * ds^2
  for (int i = 0; i + 1 < num_var; ++i) {
    columns[i].emplace_back(constraint_index, -1.0);
    columns[i + 1].emplace_back(constraint_index, 1.0);
    columns[prime_offset + i].emplace_back(constraint_index, -delta_s_);
    columns[pprime_offset + i].emplace_back(constraint_index,
                                            -delta_s_ * delta_s_ / 3.0);
    columns[pprime_offset + i + 1].emplace_back(constraint_index,
                                                -delta_s_ * delta_s_ / 6.0);

    lower_bounds[constraint_index] = 0.0;
    upper_bounds[constraint_index] = 0.0;
    ++constraint_index;
  }

  columns[0].emplace_back(constraint_index, 1.0);
  lower_bounds[constraint_index] = d_state[0];//d
  upper_bounds[constraint_index] = d_state[0];
  ++constraint_index;

  columns[prime_offset].emplace_back(constraint_index, 1.0);
  lower_bounds[constraint_index] = d_state[1];//d'
  upper_bounds[constraint_index] = d_state[1];
  ++constraint_index;

  columns[pprime_offset].emplace_back(constraint_index, 1.0);
  lower_bounds[constraint_index] = d_state[2];//d''
  upper_bounds[constraint_index] = d_state[2];
  ++constraint_index;

  const double LARGE_VALUE = 2.0;
  for (int i = 0; i < kNumParam; ++i) {
    columns[i].emplace_back(constraint_index, 1.0);
    if (i < num_var) {
      lower_bounds[constraint_index] = d_bounds[i].first;
      upper_bounds[constraint_index] = d_bounds[i].second;
    } else {
      lower_bounds[constraint_index] = -LARGE_VALUE;
      upper_bounds[constraint_index] = LARGE_VALUE;
    }
    ++constraint_index;
  }

  CHECK_EQ(constraint_index, kNumConstraint);

  // change affine_constraint to CSC format
  std::vector<c_float> A_data;
  std::vector<c_int> A_indices;
  std::vector<c_int> A_indptr;
  int ind_p = 0;
  for (int j = 0; j < kNumParam; ++j) {
    A_indptr.push_back(ind_p);
    for (const auto& row_data_pair : columns[j]) {
      A_data.push_back(row_data_pair.second);
      A_indices.push_back(row_data_pair.first);
      ++ind_p;
    }
  }
  A_indptr.push_back(ind_p);

  // offset
  double q[kNumParam];
  for (int i = 0; i < kNumParam; ++i) {
    if (i < num_var) {
      q[i] = -2.0 * FLAGS_weight_lateral_obstacle_distance *
             (d_bounds[i].first + d_bounds[i].second);
    } else {
      q[i] = 0.0;
    }
  }

  // Problem settings
  OSQPSettings* settings =
      reinterpret_cast<OSQPSettings*>(c_malloc(sizeof(OSQPSettings)));

  // Define Solver settings as default
  osqp_set_default_settings(settings);
  settings->alpha = 1.0;  // Change alpha parameter
  settings->eps_abs = 1.0e-05;
  settings->eps_rel = 1.0e-05;
  settings->max_iter = 5000;
  settings->polish = true;
  settings->verbose = FLAGS_enable_osqp_debug;

  // Populate data
  OSQPData* data = reinterpret_cast<OSQPData*>(c_malloc(sizeof(OSQPData)));
  data->n = kNumParam;
  data->m = kNumConstraint;
  data->P = csc_matrix(data->n, data->n, P_data.size(), P_data.data(),
                       P_indices.data(), P_indptr.data());
  data->q = q;
  data->A = csc_matrix(data->m, data->n, A_data.size(), A_data.data(),
                       A_indices.data(), A_indptr.data());
  data->l = lower_bounds;
  data->u = upper_bounds;

  // Workspace
  OSQPWorkspace* work = osqp_setup(data, settings);

  // Solve Problem
  osqp_solve(work);

  // extract primal results
  // prime求導符號
  for (int i = 0; i < num_var; ++i) {
    opt_d_.push_back(work->solution->x[i]);
    opt_d_prime_.push_back(work->solution->x[i + num_var]);
    opt_d_pprime_.push_back(work->solution->x[i + 2 * num_var]);
  }
  opt_d_prime_[num_var - 1] = 0.0;
  opt_d_pprime_[num_var - 1] = 0.0;

  // Cleanup
  osqp_cleanup(work);
  c_free(data->A);
  c_free(data->P);
  c_free(data);
  c_free(settings);

  return true;
}

三、偵錯過程記錄

1.程式碼缺失與完善

偵錯過程中發現各種遺漏或者錯誤，改就是了...

2.實車執行失敗案例與分析

記錄下偵錯過程中失敗的過程。

2.1 車輛遇到貼近的障礙物：一直想往上撞
計算耗時無法控制，一旦接近障礙物，由於備選軌跡很多，並且每個軌跡都要進行碰撞檢測，外加工控機效能有限，導致耗時飆至900ms，已經嚴重不符100ms的運算週期了，直接導致軌跡拼接不準確，控制和規劃無法很好銜接。

但是有一點沒想通：即使軌跡拼接出問題，為何會往障礙物上撞，暫時把這個問題擱置了，後續解決。

2.2 使用二次規劃，貼近障礙物時無解，軌跡飛掉
（a）權重不合理，導致軌跡規劃無解

發現在和障礙物平齊時，自車橫向偏移量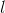總是比邊界多了0.1m....然後求解失敗

畫個圖，一切明瞭，就像那高爾夫球進洞，或者《信條》裡的逆向子彈，如果軌跡有偏差，子彈是無法退回槍膛的，只會和槍管發生碰撞。

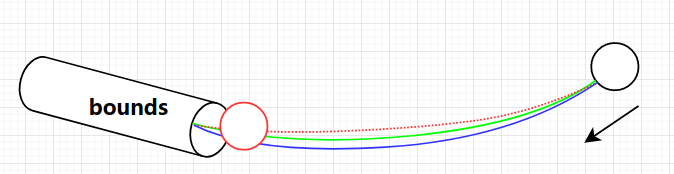
解決方法比較簡單，調節權重，提高自車和障礙物距離的權重，使得生成的軌跡適當遠離障礙物，從紅色變為綠色線。
（b）過早的轉彎，導致與障礙物發生碰撞

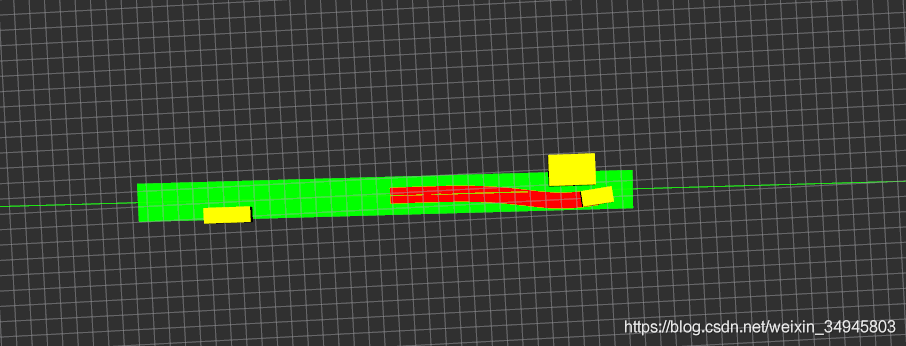
這裡問題根源還沒鎖定，可能因素有兩塊：

控制在選取預瞄距離後，過早的進行了轉向控制
規劃的軌跡的確過早轉向(這樣的話就不滿足求解約束了額，可能性不大)

不知有前輩怎麼解決的。

2.3 在特定的幾個點，軌跡直接飛掉，約束失效
車輛到某些位置會出現規劃失敗的情形，無法產生有效軌跡。為了查原因，關閉了軌跡有效性檢測，然後發現軌跡是這個diao樣子....飛掉了

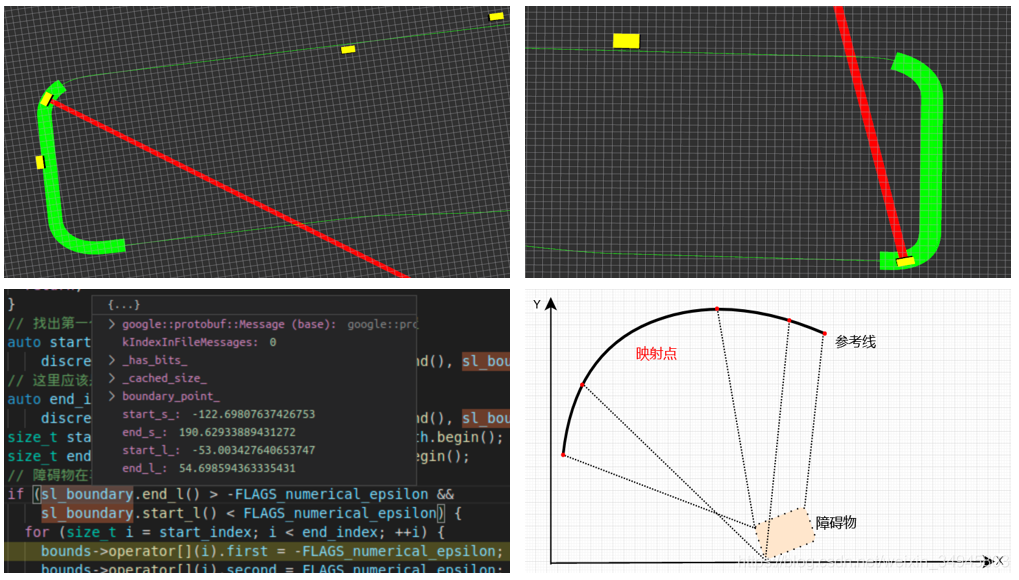
檢視該處的障礙物SL資訊，發現SL完全亂掉了。回想Frenet座標系在面對U型彎圓心處障礙物投影特點(障礙物會被極大拉伸)，在出問題的點，該位置處參考線為圓弧形，障礙物恰好位於其圓心附近，導致障礙物在frennet投影時出現了右下圖所示，存在多個投影點，其SL圖當然是要廢掉了。

總結

目前已經實現了單車道內障礙物的規避，包括繞行和減速以及停車。一套下來，雖然只是簡單的功能復現，僅僅冰山一角但已經收益頗豐，實際操作的過程難度和踩坑大幅超過了自己的預期，多虧了身邊大哥的指導和幫助，開發工作真的是需要多交流與溝通。

下一階段目標：

實現多車道的軌跡規劃，園區內可以採用偽車道，即單條referenceline進行擴幅，覆蓋整條道路寬度即可，另一個是真實的多車道多referenceline，繼續加油，一點點進步。

Lattice Planner從學習到放棄（二）：二次規劃的應用與偵錯

前言