數學是上帝描述自然的語言

出題

好吧，我承認我有些標題黨了。醒醒吧，你哪來的小學妹，作為程式猿的你身邊明明都是大老爺們！！！

言歸正傳，下面分享一道很有意思的面試題：

從前有個國王要舉辦一個宴會，準備了1000瓶酒。有個刺客要刺殺國王，在一瓶酒中下了毒，然後就被抓住了，刺客招供有一瓶酒中有毒，但是刺客自己也不知道在哪瓶酒裡下了毒。國王不想終止宴會，就想到一個辦法找死囚過來試酒從而找出毒酒，但是距離晚宴還有2個小時就要開始，而毒發身亡的時間需要1個半小時（意味著只有一次毒發的機會），國王最後想了一個辦法，只用了極少數的死囚數量就試出了毒酒，請問用了多少個死囚？是怎麼試的？（假設不管怎麼喝每瓶酒都不會喝光）

當然，本題可以說是一個思想實驗，因此忽略掉道德評判的因素。

回答

看到這個題目，大家可能就八仙過海 —— 各顯神通了。

有些人可能就會說了：這個問題還不簡單嗎？本國王財大氣粗，人力資源豐富，立馬召集1000名死囚，一人一瓶喝一口，一個半小時後死的那名死囚喝的那瓶酒就是毒酒。什麼？極少數的死囚？都說了本國王財大氣粗，1000名死囚對於本國王來說就是極少數的死囚。

當然，也有人會說既然距離晚宴還有兩個小時，而毒發時間為一個半小時，也就是說我們還有半個小時也就是30分鐘喝酒的時間。那我們來卡時間好了，我們按照保守估計來算：

假設一名死囚需要花30秒喝一瓶酒裡面的一口酒，然後再等待1分鐘喝下一瓶酒。也就是說一名死囚喝一瓶酒需要一分半的時間，三十分鐘能喝20瓶酒。因此1000瓶酒需要 1000/20 約等於 50名死囚。這還只是保守估計，比上個憨憨1000的答案不知道少了多少。然後，我們只需要看是哪個死囚死了，再根據他的死亡時間推算即可。簡直完美有木有？

首先，答案是1000的哪怕當了國王也是個憨憨國王，雖然這種方法一定可以試出哪瓶是毒酒。其次，根據死亡時間推斷的肯定是偵探懸疑題材類的小說或者影視作品看多了。根據死亡時間推斷似乎有一定的道理，但是每個人的體質是不一樣的，所以毒發的時間也是不一樣的， 一個半小時的時間只是個大概的時間，所以50的答案也不完美，甚至很可能會出錯。而一旦出錯，就是幾百上千條人命。

那麼這個題目該如何解呢？

我們都知道一般的解題教學都是先給出思路以及解題過程，再得出答案。這裡我們反其道而行之，先給出答案：

試出1000瓶葡萄酒中的一瓶毒酒所需要的死囚數為：log1000(以2為底)，答案應該為9點多，但是人不能論半個，所以向上取整也就是10名。

這個時候可能大家就會有一個疑問了：log1000(以2為底)是9點多是怎麼算出來的？？？

懂對數運算的小夥伴們下面就可以忽略了

這裡先給大家簡單介紹一下對數運算，以下是百度百科的官方解釋：

我們看這兩句就好了：

1. 對數是對求冪的逆運算。
2. 如果a的x次方等於N（a>0，且a≠1），那麼數x叫做以a為底N的對數（logarithm），記作x=loga N。其中，a叫做對數的底數，N叫做真數。

舉個栗子好了：

log1(以2為底)的值是多少？在這個栗子中2為底數，1為真數，答案為x，也就是2的多少次方是1，答案就是多少。而我們都知道除0以外的任何數的0次方都為1，所以log1(以2為底)的值是0。

以下是logx(以2為底)的函數圖(右半部分)：

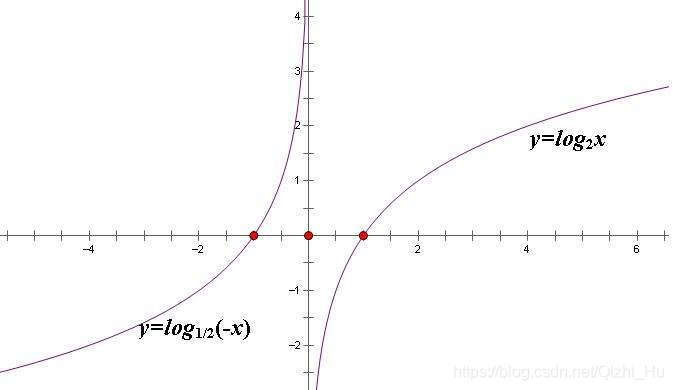
那麼，log1000(以2為底)到底是多少呢？

答：2的多少次方是1000就是多少！！！

而2的9次方是512，2的10次方是1024（熟悉的1024），所以log1000(以2為底)位於 9 - 10 之間，也就是9點多。

看到這裡你可能還是很懵。好吧，log1000(以2為底)這個的值我知道是怎麼算出來的了，但是這個log1000(以2為底)是怎麼得出來的，而且這個答案為10比起1000或者說是50也太少了吧，簡直不科學，不可能呀！

不要急，這個就是正確答案。至於箇中緣由，請聽我接下來娓娓道來！！！

資訊熵

如果用一句話來概括本文中的問題：無非是國王想要弄清楚1000瓶酒中哪一瓶是毒酒，國王不確定1000瓶酒中哪一瓶是毒酒 好像是句廢話 。我們往上走一層，也就是說國王想要弄清楚一件非常非常不確定的事情。

如果從資訊的角度來理解，一件事情的不確定性就等於它的資訊量，而我們通常用資訊熵來實現資訊的度量（具體可以參照吳軍博士《數學之美》的第6章<資訊的度量和作用>）

《數學之美》pdf 百度網路硬碟連結分享
連結：https://pan.baidu.com/s/1dQ08nWsSmyuMDhesIYv_Vw
提取碼：yxaf

看起來資訊熵的概念似乎很玄學。但是沒關係，吳軍博士在《數學之美》中舉了一個很通俗易懂的例子，以下是原文（寫不動了，最近缺乏小夥伴們的支援和鼓勵，容我偷個小懶）：

來看一個例子。2010 年舉行了世界盃足球賽，大家都很關心誰會是冠軍。假如我錯過了看世界盃，賽後我問一個知道比賽結果的觀眾「哪支球隊是冠軍」?他不願意直接告訴我，而讓我猜，並且我每猜一次，他要收一元錢才肯告訴我是否猜對了，那麼我需要付給他多少錢才能知道誰是冠軍呢?我可以把球隊編上號，從1到32，然後提問:「 冠軍的球隊在1-16號中嗎?」假如他告訴我猜對了，我會接著問:「冠軍在 1-8號中嗎?」假如他告訴我猜錯了，我自然知道冠軍隊在9-16號中。這樣只需要五次，我就能知道哪支球隊是冠軍。所以，誰是世界盃冠軍這條訊息的資訊量只值5塊錢。

是不是跟二分查詢的理念是一樣的呢？

二分查詢的話，可以檢視我的這篇部落格的第一章就是了：
肝了幾萬字，送給看了《演演算法圖解》卻是主攻Java的你和我（上篇）

而二分查詢的時間複雜度為logN(以2為底)。在上文中，假設每支球隊奪冠概率相同的話，如果要保證一定能猜出32只球隊中的冠軍隊伍，我只需要5次，也就是log32(以2為底)。那麼，國王想要一定能找出1000瓶毒酒中的哪一瓶毒酒，只需要查詢log1000(以2為底)次，也就是9點多次。因為一定要找出，9次可能找不完，所以需要10次。

這個時候可能很多小夥伴就開始躍躍欲試了：我知道了，我知道了

我們來把1000瓶酒按照 1 - 1000進行編號，那我們只需要10次就可以試出毒酒了：

1. 第一次，安排1名死囚，分別品嚐編號為 1-500 的酒。如果這名死囚毒發身亡，則毒酒在編號為1 - 500酒中；反之，則在另外500瓶酒中。
2. 第二次，再安排1名死囚，分別品嚐編號為 1 - 250 的酒。（在這裡，我們也假設這名死囚毒發身亡）。
3. 第三次，再次安排1名死囚，分別品嚐編號為 1 - 125瓶的酒。（這裡，我們還是假設這名死囚毒發身亡）。
4. 第四次，再再次安排1名死囚，分別品嚐編號為 1 - 63瓶的酒。（在這裡，我們還是假設這名死囚毒發身亡）。
5. 第五次，再再再次安排1名死囚，分別品嚐編號為 1 - 32瓶的酒。（在這裡，我們還是假設這名死囚毒發身亡。如果沒有人毒發身亡毒酒就在另外的31瓶酒裡。）。

好了，到了久違的32。根據上文我們可以知道還需要5次就一定可以判斷出毒酒是哪瓶！總次數，也就是 5 + 5 = 10次！！！

那麼，按照這種方法需要的死囚人數最多為10名（畢竟如果這名死囚沒有毒發身亡的話，就可以接著試酒）。

哦，原來這個就是正確答案的由來呀！！！

不過這個時候可能有小夥伴就會發現不對勁了

等等，這個方法我確實是理解了。但是這樣的話：

• 耗時：一個半小時 * 10 = 15個小時。

what???需要十五個小時，那我等到能吃酒席的話，黃花菜都涼了。

所以本章節講的全都是廢話嗎？

當然不是！

那如果不是廢話的話，為什麼完全無法達到想要的效果呢？

因為我們現在還停留在十進位制的世界。

下面，歡迎來到二進位制的世界！！！

二進位制

如果你看到上圖中的話，不禁心中生出一個疑問：那另外八種人呢？那麼不好意思，你屬於不懂二進位制的人，因為二進位制中的2表示為 10。

曾幾何時，我以為這句話只是單純用來裝（A和C之間）來用的。

曾幾何時，我也天真的認為十進位制天然要比二進位制要高階得多 。

但其實不然！

當然，在我的這篇部落格 實現兩個數互換的八種方法 的<互斥或>章節中曾經提到過：

計算機中沒有我們所謂的2、3、4、5 … 100 … 1000 … ，計算機中有的只是0和1，逢二便進一。

那麼，二進位制和資訊熵有啥子關聯嗎？我們試著追根溯源：原來，資訊熵的概念是1948年夏農在他那非常著名的論文《通訊的數學原理》中提出來的。而夏農並不是用次數(比如猜出32球隊中的冠軍隊伍為5次、1000瓶毒酒需要10次)來度量資訊量的，而是用位元(Bit)這個概念！

那麼問題來了，什麼是位元呢？

其實，一個位元就是一個二進位制位！

就拿吳軍博士舉的這個球隊的栗子好了。

這裡我們為了節省空間，就假設只有8只球隊好了，32支球隊、64支球隊都可以以此類推。

經過上述分析，猜出8支隊伍中冠軍隊伍的資訊熵為log8(以2為底)，也就是3位元，3個二進位制位。而獲得冠軍隊伍可能的結果：總共為8種情況。剛好可以用3個二進位制位表示。

如下表，3個二進位制位剛好可以表示8種情況：

十進位制	二進位制
0	0 0 0
1	0 0 1
2	0 1 0
3	0 1 1
4	1 0 0
5	1 0 1
6	1 1 0
7	1 1 1

或者說，我們剛好可以用3個二進位制位給這8支球隊編號。（二進位制是從0開始計數）

那麼，按照二進位制的思維該如何解這個「國王試毒酒」問題呢？

破案

大家好，我是狄仁傑，我來破案了。

為了方便大家思考，我們從頭開始分析

1. 假設是1瓶酒，因為這瓶酒肯定是毒酒，所以需要0名死囚品嚐這一瓶酒。
2. 假設是2瓶酒，我們不確定哪瓶酒有毒。只需要一名死囚品嚐其中一瓶酒：若死囚身亡，則品嚐的酒有毒；反之，則另一瓶酒有毒。
3. 假設是3瓶酒，我們不確定哪瓶酒有毒。這個時候一名死囚明顯就不夠用了撒，就需要再加一名死囚。

所以，我們通過以上分析可以得出：一名死囚所能試出毒酒的最多瓶數為2瓶，也就是2的1次方。換言之，2瓶酒的資訊熵為log2(以2為底)，也就是1位元，為一個二進位制位。

那麼，到底該怎麼試呢？

這裡，我們將一名死囚對應一個二進位制位，將酒分別用二進位制進行編號。如下表：

十進位制	二進位制位1
酒的編號	死囚甲
0	0
1	1

通過上述分析，我們已經知道了：在兩瓶酒的情況下，只要死囚甲隨便選擇一瓶喝就可以試出哪一瓶是毒酒。

因為二進位制只有0和1兩種情況，而死囚對於一瓶酒也只有兩種情況：喝，或者不喝。

而作為創造萬物的程式設計師，這裡我們可以很容易的設定一個規則：當死囚對應的二進位制位為1時喝，為0時不喝（當然，你也可以反過來）。也就是說，在上表中，編號為0的酒，我們簡稱酒0，不讓死囚甲喝；而酒1則死囚甲喝。

若是，死囚甲毒發身亡，則酒1有毒；反之，則酒0有毒。

同樣的，2名死囚可以表示2的2次方，也就是試出4瓶酒；或者說，4瓶酒的資訊熵為log4(以2為底數)也就是2Bit，2個二進位制位。

我們也可以用表格表示出來：

十進位制	二進位制位2	二進位制位1
酒的編號	死囚乙	死囚甲
0	0	0
1	0	1
2	1	0
3	1	1

同樣的，死囚對應的二進位制位為1時喝，為0時不喝。也就是說，死囚甲需要喝酒1和酒3，死囚乙需要喝酒2和酒3。

那麼，如果這樣的話，我們該如何根據身亡情況來判定毒酒呢？

其實，很簡單：如果某名死囚身亡，那麼毒酒一定在他喝的那些酒中；反之，如果某名死囚沒身亡，那麼毒酒一定不在他喝的那些酒中。

而根據我們的規則：某名死囚對應的二進位制位為1，則表示喝；為0，則表示不喝。所以，每瓶酒是毒酒所對應的情況分別為：

十進位制	二進位制位2	二進位制位1
酒的編號	死囚乙(狀態)	死囚甲(狀態)
0	0 (生)	0 (生)
1	0 (生)	1 (死)
2	1 (死)	0 (生)
3	1 (死)	1 (死)

顯然：

1. 若是甲乙雙生，則對應的二進位制位為00，也就是酒0為毒酒。
2. 若是乙生甲死，則對應的二進位制位為01，也就是酒1為毒酒。
3. 若是乙死甲生，則對應的二進位制位為10，也就是酒2為毒酒。
4. 若是甲乙雙死，則對應的二進位制位為11，也就是酒3為毒酒。

同樣的，三名死囚可以表示出2的3次方也就是8瓶酒。

十進位制	二進位制位3	二進位制位2	二進位制位1
酒的編號	死囚丙	死囚乙	死囚甲
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

同樣的，死囚所對應的二進位制位為1，表示喝；為0，則表示不喝。

• 若死囚甲乙丙都死，則他們的二進位制位全都表示為1，也就是 111。對應十進位制的7，也就是酒7為毒酒。
• 若死囚甲乙丙都不死，則他們的二進位制位全都表示為0，也就是 000。對應十進位制的0，也就是酒0為毒酒。

那麼通過以上種種，我們來類推一下

1. 試出1瓶酒中的一瓶毒酒，需要0名死囚，也就是log1(以2為底)。
2. 試出2瓶酒中的一瓶毒酒，需要1名死囚，也就是log2(以2為底)。
3. 試出3瓶酒中的一瓶毒酒，需要2名死囚，也就是log3(以2為底)，向上取整為2。
4. 試出4瓶酒中的一瓶毒酒，需要2名死囚，也就是log4(以2為底)。
5. 試出5瓶酒中的一瓶毒酒，需要3名死囚，也就是log5(以2為底),向上取整為3。
   …
6. 試出8瓶酒中的一瓶毒酒，需要3名死囚，也就是log8(以2為底)。
   …

所以，試出1000瓶酒中的一瓶毒酒，需要10名死囚，也就是log1000(以2為底)，,向上取整為10。

怎麼樣？感受到二進位制的神奇和美妙了嗎？

迴歸數學

當然，神奇歸神奇，那麼到底為啥子可以這樣呢？為此，我還特意請教了一位數學專業的小學妹。她從集合的角度分析倒給了我一個全新的思考視角。

一名死囚可以表示的情況為2種：

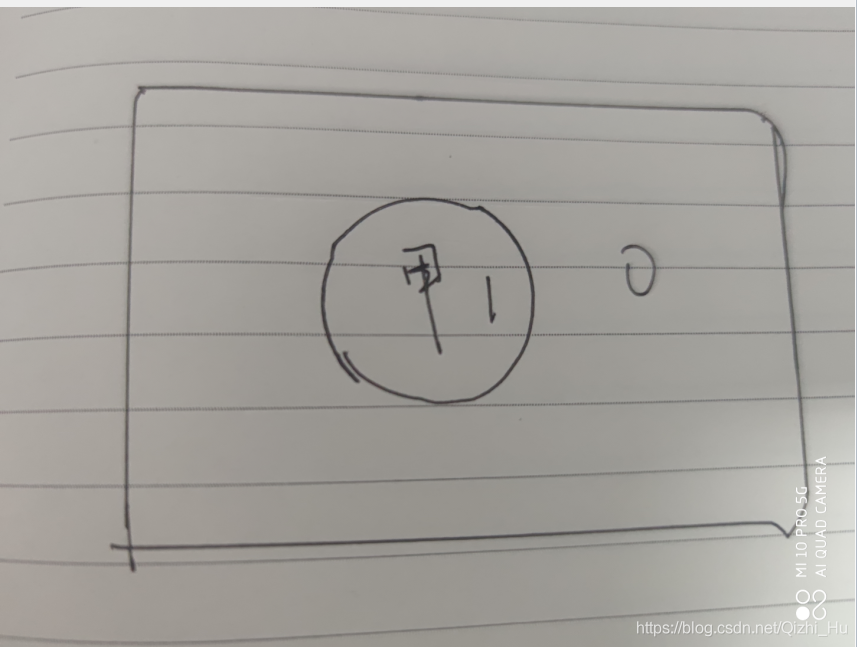
兩名死囚可以表示的情況為4種：

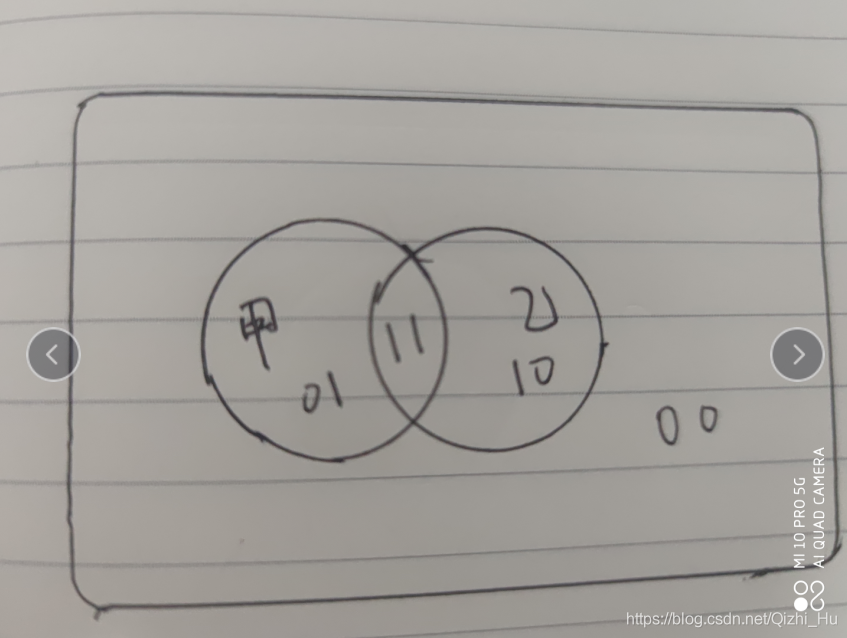
三名死囚可以表示的情況為8種：

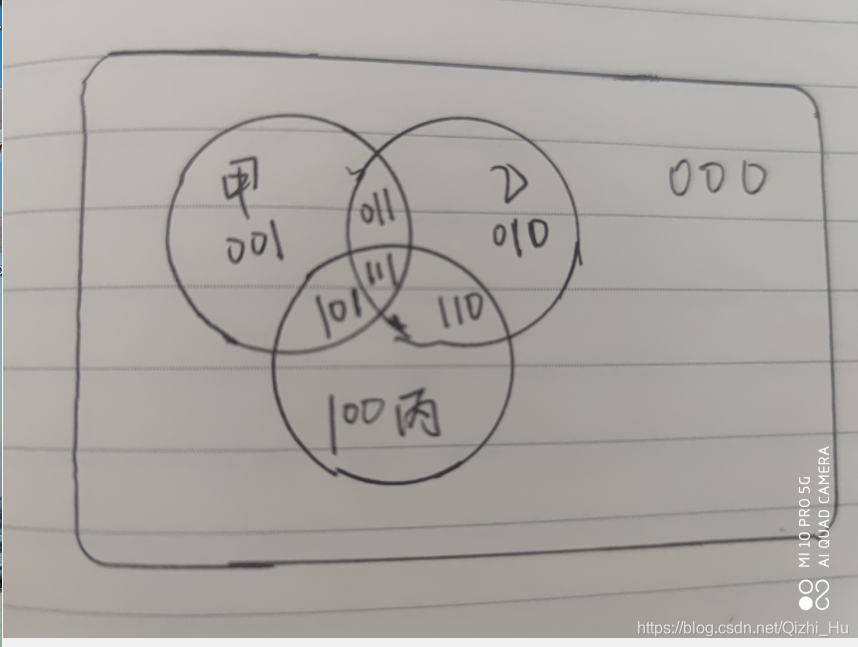
以此類推即可。

其實這個數學問題，被稱為 冪集，也就是求集合中所有的子集（包括全集和空集）構成的集族。因為每個子集都有兩種情況：選，或者不選。所以，n個子集所對應的情況為： 2的n次方，而一種情況恰好對應著唯一的一瓶酒。是不是和之前的分析有著異曲同工之妙呢？

關於圖片：沒辦法，畫圖軟體處理不好圖層之間的關係，我就只好手畫了，哈哈。

最後

不知不覺，一篇部落格就肝到了凌晨一點半左右：

工作以後，可以用來寫部落格的時間也變少了。各位小夥伴們，如果覺得這篇部落格寫的還不錯的話，歡迎各位點贊、評論以及加關注哦。這樣本博主才更有動力給大家帶來更多的優質部落格。