LeetCode——二分專題

文章目錄

- LeetCode——二分

LeetCode——二分

69. x 的平方根

實現 int sqrt(int x) 函數。

計算並返回 x 的平方根，其中 x 是非負整數。

由於返回型別是整數，結果只保留整數的部分，小數部分將被捨去。

範例 :

輸入: 4
輸出: 2

輸入: 8
輸出: 2
說明: 8 的平方根是 2.82842..., 
     由於返回型別是整數，小數部分將被捨去。

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x;
        while(l < r){
            int mid = l + (long long)r + 1>> 1;
            if(mid <= x/mid) l = mid;  // 查詢t^2 <= x
            else r = mid - 1;
        }
        return l;
    }
};

35. 搜尋插入位置

給定一個排序陣列和一個目標值，在陣列中找到目標值，並返回其索引。如果目標值不存在於陣列中，返回它將會被按順序插入的位置。

你可以假設陣列中無重複元素。

範例 :

輸入: [1,3,5,6], 5
輸出: 2

輸入: [1,3,5,6], 2
輸出: 1

輸入: [1,3,5,6], 7
輸出: 4

輸入: [1,3,5,6], 0
輸出: 0

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums.empty() || target > nums.back()) return nums.size();
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;  // 查詢t>=x的第一個數
            else l = mid + 1; 
        }
        return l;
    }
};

34. 在排序陣列中查詢元素的第一個和最後一個位置

給定一個按照升序排列的整數陣列 nums，和一個目標值 target。找出給定目標值在陣列中的開始位置和結束位置。

你的演演算法時間複雜度必須是 O(log n) 級別。

如果陣列中不存在目標值，返回 [-1, -1]。

範例 :

輸入: nums = [5,7,7,8,8,10], target = 8
輸出: [3,4]

輸入: nums = [5,7,7,8,8,10], target = 6
輸出: [-1,-1]

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.empty()) return {-1, -1};
        return {getFirst(nums, target), getLast(nums, target)};
    }
    int getFirst(vector<int>& nums, int target){
        int l = 0, r = nums.size()-1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        return nums[l] != target ? -1 : l;
    }
    int getLast(vector<int>& nums, int target){
        int l = 0, r = nums.size()-1;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        return nums[l] != target ? -1 : l;
    }
};

74. 搜尋二維矩陣

編寫一個高效的演演算法來判斷 m x n 矩陣中，是否存在一個目標值。該矩陣具有如下特性：

每行中的整數從左到右按升序排列。
每行的第一個整數大於前一行的最後一個整數。

範例：

輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
輸出：true

輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
輸出：false

輸入：matrix = [], target = 0
輸出：false

注：二維陣列下標轉換
在這裡插入圖片描述

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.empty() || matrix[0].empty()) return false;
        int n = matrix.size(), m = matrix[0].size();
        int l = 0, r = n*m-1;
        while(l < r){
            int mid = l + r >> 1;
            if(matrix[mid/m][mid%m] >= target) r = mid;  // t>=x
            else l = mid + 1; 
        }
        return matrix[l/m][l%m] == target ? true : false;
    }
};

153. 尋找旋轉排序陣列中的最小值

假設按照升序排序的陣列在預先未知的某個點上進行了旋轉。

( 例如，陣列 [0,1,2,4,5,6,7] 可能變為 [4,5,6,7,0,1,2] )。

請找出其中最小的元素。

你可以假設陣列中不存在重複元素。

範例 :

輸入: [3,4,5,1,2]
輸出: 1

輸入: [4,5,6,7,0,1,2]
輸出: 0

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums.back()) r = mid;  // nums[t]<=nums.back
            else l = mid + 1;
        }
        return nums[l]; 
    }
};

33. 搜尋旋轉排序陣列

給你一個升序排列的整數陣列 nums ，和一個整數 target 。

假設按照升序排序的陣列在預先未知的某個點上進行了旋轉。（例如，陣列 [0,1,2,4,5,6,7] 可能變為 [4,5,6,7,0,1,2] ）。

請你在陣列中搜尋 target ，如果陣列中存在這個目標值，則返回它的索引，否則返回 -1 。

範例：

輸入：nums = [4,5,6,7,0,1,2], target = 0
輸出：4

輸入：nums = [4,5,6,7,0,1,2], target = 3
輸出：-1

輸入：nums = [1], target = 0
輸出：-1

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty()) return -1;
        // 找到最小值
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums.back()) r = mid;  // nums[t] <= nums.back()
            else l = mid + 1;
        }
        if(target <= nums.back()) r = nums.size() - 1;
        else l = 0, r--;
        // 單調二分
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;  // t >= x
            else l = mid + 1;
        }
        return nums[l] == target ? l : -1;
    }
};

278. 第一個錯誤的版本

你是產品經理，目前正在帶領一個團隊開發新的產品。不幸的是，你的產品的最新版本沒有通過品質檢測。由於每個版本都是基於之前的版本開發的，所以錯誤的版本之後的所有版本都是錯的。

假設你有 n 個版本 [1, 2, …, n]，你想找出導致之後所有版本出錯的第一個錯誤的版本。

你可以通過呼叫 bool isBadVersion(version) 介面來判斷版本號 version 是否在單元測試中出錯。實現一個函數來查詢第一個錯誤的版本。你應該儘量減少對呼叫 API 的次數。

範例:

給定 n = 5，並且 version = 4 是第一個錯誤的版本。

呼叫 isBadVersion(3) -> false
呼叫 isBadVersion(5) -> true
呼叫 isBadVersion(4) -> true

所以，4 是第一個錯誤的版本。

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int l = 1, r = n;
        while(l < r){
            int mid = l + (long long)r >> 1;  // n為最大整數，溢位
            if(isBadVersion(mid)) r = mid;
            else l = mid + 1; 
        }
        return l;
    }
};

162. 尋找峰值

峰值元素是指其值大於左右相鄰值的元素。

給定一個輸入陣列 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素並返回其索引。

陣列可能包含多個峰值，在這種情況下，返回任何一個峰值所在位置即可。

你可以假設 nums[-1] = nums[n] = -∞。

範例 :

輸入: nums = [1,2,3,1]
輸出: 2
解釋: 3 是峰值元素，你的函數應該返回其索引 2。

輸入: nums = [1,2,1,3,5,6,4]
輸出: 1 或 5 
解釋: 你的函數可以返回索引 1，其峰值元素為 2；
     或者返回索引 5， 其峰值元素為 6。
說明:
你的解法應該是 O(logN) 時間複雜度的。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] < nums[mid + 1]) l = mid + 1;
            else r = mid;
        }
        return l;
    }
};

287. 尋找重複數

給定一個包含 n + 1 個整數的陣列 nums，其數位都在 1 到 n 之間（包括 1 和 n），可知至少存在一個重複的整數。假設只有一個重複的整數，找出這個重複的數。

範例 :

輸入: [1,3,4,2,2]
輸出: 2

輸入: [3,1,3,4,2]
輸出: 3
說明：
不能更改原陣列（假設陣列是唯讀的）。
只能使用額外的 O(1) 的空間。
時間複雜度小於 O(n2) 。
陣列中只有一個重複的數位，但它可能不止重複出現一次。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size()-1;
        int l = 1, r = n;
        while(l < r){
            int cnt = 0;
            int mid = l + r >> 1;
            for(int x : nums)
                if(x <= mid) cnt++;  // 統計中位數及左邊數位的個數
            if(cnt > mid) r = mid;
            else l = mid+1; 
        }
        return l;
    }
};

275. H 指數 II

給定一位研究者論文被參照次數的陣列（被參照次數是非負整數），陣列已經按照升序排列。編寫一個方法，計算出研究者的 h 指數。

h 指數的定義: 「h 代表「高參照次數」（high citations），一名科研人員的 h 指數是指他（她）的（N 篇論文中）總共有 h 篇論文分別被參照了至少 h 次。（其餘的 N - h 篇論文每篇被參照次數不多於 h 次。）"

範例:

輸入: citations = [0,1,3,5,6]
輸出: 3 
解釋: 給定陣列表示研究者總共有 5 篇論文，每篇論文相應的被參照了 0, 1, 3, 5, 6 次。
     由於研究者有 3 篇論文每篇至少被參照了 3 次，其餘兩篇論文每篇被參照不多於 3 次，所以她的 h 指數是 3。

說明:
如果 h 有多有種可能的值 ，h 指數是其中最大的那個。

思路：

至少存在h個數≥h
即看倒數第h個數是否≥h

class Solution {
public:
    int hIndex(vector<int>& nums) {
        int l = 0, r = nums.size();
        while(l < r){
            int mid = l + r + 1>> 1;
            if(nums[nums.size() - mid] >= mid) l = mid;  // 左邊都滿足nums[h]>=h,判斷倒數第h個數是否≥h
            else r = mid - 1;
        }
        return l;
    }
};

參考連結：

擴充套件分類

練習題

題型一：在陣列中查詢符合條件的元素的下標
一般而言這個陣列是有序的，也可能是半有序的（旋轉有序陣列或者山脈陣列）。

題目	提示與題解
704. 二分查詢(簡單)	二分查詢的最原始問題，使用本題解介紹的方法就要注意，需要後處理。
34. 在排序陣列中查詢元素的第一個和最後一個位置(中等)	查詢邊界問題，題解（有視訊講解）。
33. 搜尋旋轉排序陣列(中等)	題解，利用區域性單調性，逐步縮小搜尋區間（其它問題類似）
81. 搜尋旋轉排序陣列 II(中等)	題解
153. 尋找旋轉排序陣列中的最小值(中等)	題解
154. 尋找旋轉排序陣列中的最小值 II(中等)	題解
300. 最長上升子序列(中等)	特別經典的一道「動態規劃」，二分查詢的思路是基於「動態規劃」的狀態定義得到，程式碼很像第 35 題，題解。
275. H 指數 II(中等)	題解
852. 山脈陣列的峰頂索引（簡單）	利用區域性單調性，逐步縮小搜尋區間。
1095. 山脈陣列中查詢目標值(中等)	官方題解（有視訊講解），題解
4. 尋找兩個正序陣列的中位數(困難))	官方題解（有視訊講解），題解
658. 找到 K 個最接近的元素(中等)	題解，這個問題二分的寫法需要做複雜的分類討論，可以放在以後做

題型二：在一個有範圍的區間裡搜尋一個整數
定位一個有範圍的整數，這件事情也叫「二分答案」或者叫「二分結果」。如果題目要求的是一個整數，這個整數有明確的範圍，可以考慮使用二分查詢。

題目	提示與題解
69. 平方根（簡單）	題解，在一個整數範圍裡查詢一個整數，也是二分查詢法的應用場景。
287. 尋找重複數（中等）	題解，在一個整數範圍裡查詢一個整數。這個問題二分查詢的解法很反常規，知道即可。
374. 猜數位大小（簡單）	題解
1300. 轉變陣列後最接近目標值的陣列和	題解

題型三：複雜的二分查詢問題（判別條件需要遍歷陣列）
「力扣」上還有這樣一類問題：目標變數和另一個變數有相關關係（一般而言是線性關係），目標變數的性質不好推測，但是另一個變數的性質相對容易推測（滿足某種意義上的單調性）。這樣的問題的判別函數通常會寫成一個函數的形式。

這一類問題可以統稱為「 最大值極小化 」問題，最原始的問題場景是木棍切割問題，這道題的原始問題是「力扣」第 410 題。

解題的思路是這樣的：

分析出題目要我們找一個整數，這個整數有範圍，所以可以用二分查詢；
分析出單調性，一般來說是一個變數 a 的值大了，另一個變數 b 的值就變小，而「另一個變數的值」 b 有限制，因此可以通過調整 a 的值達到控制 b 的效果；
這一類問題的題目條件一定會給出連續、正整數這樣的關鍵字，如果沒有，問題場景也一定蘊含了這兩個關鍵資訊。

以下給出的問題無一例外。

題目	提示與題解
410. 分割陣列的最大值（困難）	題解
875. 愛吃香蕉的珂珂（中等）	題解
LCP 12. 小張刷題計劃（中等）	（題解在第 410 題題解裡）
1482. 製作 m 束花所需的最少天數（中等）	（題解在第 1300 題題解裡）
1552. 兩球之間的磁力（中等）

LeetBook總結

704. 二分查詢(簡單)

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty()) return -1;
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        return nums[l] == target ? l : -1; 
    }
};

374. 猜數位大小

/** 
 * Forward declaration of guess API.
 * @param  num   your guess
 * @return 	     -1 if num is lower than the guess number
 *			      1 if num is higher than the guess number
 *               otherwise return 0
 * int guess(int num);
 */

class Solution {
public:
    int guessNumber(int n) {
        int l = 1, r = n;
        while(l < r){
            int mid = l + (long long)r >> 1;
            int res = guess(mid);
            if(res <= 0) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};

81. 搜尋旋轉排序陣列 II(中等)
【分析】與lc33類似，多了重複數位的情況，只需去掉旋轉陣列結尾和開頭相同的部分，剩下的與lc33完全相同。

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        if(nums.empty()) return false;
        // 去掉結尾和開頭相同的部分
        int t = nums.size() - 1;
        while(t > 0 && nums[t] == nums[0]) t--;
        // 找最小值
        int l = 0, r = t;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums[t]) r = mid;
            else l = mid + 1;
        }
        if(target <= nums[t]) r = t;  // 答案在右邊
        else l = 0, r--;  // 答案在左邊
        // 單調二分
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        return nums[l] == target;
    }
};

154. 尋找旋轉排序陣列中的最小值 II(中等)

【分析】與lc153類似，多了重複數位的情況，只需去掉旋轉陣列結尾和開頭相同的部分，剩下的與lc153完全相同。

class Solution {
public:
    int findMin(vector<int>& nums) {
        int t = nums.size()-1;
        while(t > 0 && nums[t] == nums[0]) t--;  // 去掉結尾與開頭相同的部分
        int l = 0, r = t;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums[t]) r = mid;
            else l = mid + 1;
        }
        return nums[l];
    }
};

852. 山脈陣列的峰頂索引（簡單）

【思路】找峰頂，判斷是否有 M ≥ M+1

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= nums[mid+1]) r = mid;  // M >= M+1
            else l = mid + 1;
        }
        return l;
    }
};

1095. 山脈陣列中查詢目標值（中等）

【思路】先找到峰頂，左右區間找target

  /**
   * // This is the MountainArray's API interface.
   * // You should not implement it, or speculate about its implementation
   * class MountainArray {
   *   public:
   *     int get(int index);
   *     int length();
   * };
   */
  
  class Solution {
  public:
      int findInMountainArray(int target, MountainArray &nums) {
          // 找到峰頂，最大值
          int l = 0, r = nums.length() - 1;
          while(l < r){
              int mid = l + r >> 1;
              if(nums.get(mid) >= nums.get(mid+1)) r = mid;
              else l = mid + 1;
          }
          int t = l;  // t為峰頂
          // 在左側遞增區間找target
          l = 0, r = t;
          while(l < r){
              int mid = l + r >> 1;
              if(nums.get(mid) >= target) r = mid;
              else l = mid + 1; 
          }
          if(nums.get(l) == target) return l;
          // 在右側遞減區間找target
          l = t + 1, r = nums.length() - 1;
          while(l < r){
              int mid = l + r >> 1;
              if(nums.get(mid) <= target) r = mid;
              else l = mid + 1;
          }
          if(nums.get(l) == target) return l;
          else return -1;
      }
  };

658. 找到 K 個最接近的元素（中等）

【思路】只尋找左邊界即可。

假設 mid 是左邊界，則當前區間覆蓋的範圍是 [mid, mid + k -1]. 如果發現 a[mid] 與 x 距離比 a[mid + k] 與 x 的距離要大，說明解一定在右側，否則在左側。

class Solution {
public:
    vector<int> findClosestElements(vector<int>& nums, int k, int x) {
        int l = 0, r = nums.size() - k;  // 保證mid+k不超出範圍
        while(l < r){
            int mid = l + r >> 1;
            if(x - nums[mid] <= nums[mid+k] - x) r = mid;
            else l = mid + 1; 
        }
        return vector<int>(nums.begin()+l, nums.begin()+l+k);
    }
};

1300. 轉變陣列後最接近目標值的陣列和
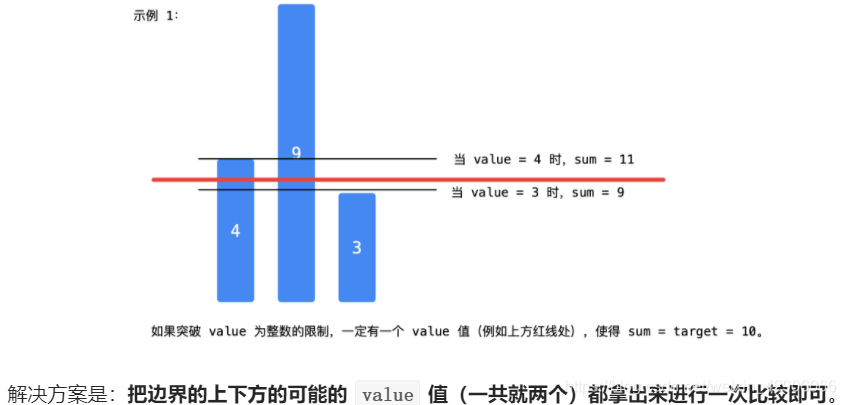
【思路】二分查詢確定這個整數值（閾值越大，轉變陣列和越大，具有單調性，可用二分，對比lc658）
如果選擇一個閾值 value ，使得它對應的 sum 是第 1 個大於等於 target 的，那麼目標值可能在 value 也可能在 value - 1
在這裡插入圖片描述

 class Solution {
 public:
     int findBestValue(vector<int>& arr, int target) {
         int l = 0, r = 0;
         for(int num : arr)
             r = max(r, num);  // 找陣列中的最大值作為右邊界
         // 二分找到第一個大於等於target的閾值val
         while(l < r){  
             int mid = l + r >> 1;
             int sum = calSum(arr, mid);
             if(sum >= target) r = mid;
             else l = mid + 1;
         }
         // 找最接近target左右兩邊最小的數
         int sum1 = calSum(arr, l - 1);
         int sum2 = calSum(arr, l);
         if(target - sum1 <= sum2 - target)  // k-x1 <= x2-k
             return l - 1;
         return l;
     }
     int calSum(vector<int>& arr, int val){  // 計算轉變陣列的和
         int sum = 0;
         for(int num : arr)
             sum += min(num, val);
         return sum;
     }
 };