前導

要學習莫比烏斯函數 需要學習 到 積性函數，深度理解尤拉篩。

先說說什麼是積性函數吧。

積性函數

其實積性函數非常好理解，
定義

積性函數：若gcd(a,b)=1，且滿足f(ab)=f(a)f(b)，則稱f(x)為積性函數
完全積性函數：對於任意正整數a，b，都滿足f(ab)=f(a)f(b)，則稱f(x)為完全積性函數
性質

1.若f(n),g(n)均為積性函數，則函數h(n)=f(n)g(n)也是積性函數
2.若f(n)為積性函數，則函數c*f(n)(c是常數)也是積性函數，反之一樣
3.任何積性函數都能應用線性篩，在O(n)時間內求出1~n項(莫比烏斯就要用到)，畫素數，尤拉函數等都是 積性函數。

知道這些之後，我們就來看莫比烏斯函數。

莫比烏斯函數

定義：
莫比烏斯函數主要是個分段函數。

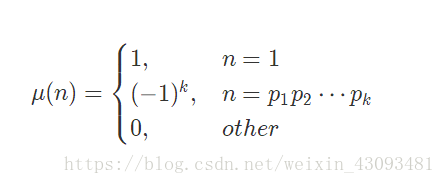
性質：
1.對於任意正整數n，${\sum }_{d|n}^n\mu (d)=[n=1]$ 。（[n==1]表示只有當n=1成立時，返回值為1；否則，值為0；(這個就是用μ是容斥係數的性質可以證明)(PS:這一條性質是莫比烏斯反演中最常用的)

2.對於任意正整數n，${\sum }_{d|n}^n\frac{\mu (d)}{d}=\frac{\varphi (n)}{n}$ （這個性質很奇妙，它把尤拉函數和莫比烏斯函數結合起來）

強烈建議 ： 深度理解完這兩條性質之後，在去看莫比烏斯反演，要不莫比烏斯反演不容易懂。

至於如何求莫比烏斯函數：我們知道莫比烏斯函數跟尤拉函數一樣都是積性函數，所以我們可以同 尤拉篩一樣吧莫比烏斯函數篩出來。

void get_mu(ll n){
	mu[1]=1;// 存放 莫比烏斯函數；
	//isprime[] 存放 是否是質數
	//prime[]  存放  質數 
	for(int i=2;i<=n;i++){
		if(!isprime[i]) {
			prime[++cnt]=i;
			mu[i]=-1;
		}
		for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
			isprime[i*prime[j]]=1;
			if(i%prime[j]==0){mu[i*prime[j]]=0;break;}//也可以直接break 因為裡面本來存的就是0 
			else mu[i*prime[j]]=-mu[i];			
		}		
	} 
}

莫比烏斯反演

我只是掌握皮毛，有深層次的理解在更新，有更好的理解也可以分享給我哦~~~。 不勝感激！

莫比烏斯反演的引入：

若 $F(n)={\sum }_{d|n}^{n}f(d)$.

那麼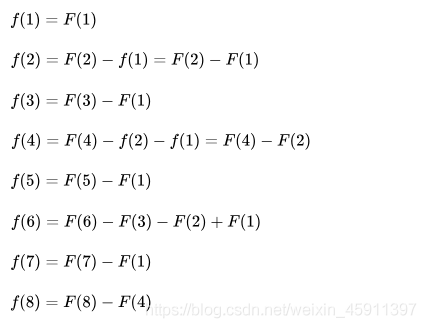
從中，可以看出，若 n=p²(p是質數)那麼$F\left(p\right)=f\left(1\right)+f\left(p\right),F\left(n\right)=f\left(1\right)+f\left(p\right)+f\left(p^2\right)$,所以 $f\left(n\right)=F\left(p^2\right)-F\left(p\right)$
通過推廣我們可以得到就像n=8，(！=p²) 他也滿足這個式子

$f\left(n\right)={\sum }_{d|n}^{n}u\left(d\right)F\left(\frac{n}{d}\right)$

根據上個推廣的來的式子我們 就可以說 莫比烏斯反演定理了。

莫比烏斯反演定理

設 $f\left(n\right)$ 和$g\left(n\right)$是定義在正整數集合上的兩個函數定義如下:
若函數$f\left(n\right)$函數:
$f\left(n\right)={\sum }_{d|n}^{n}g\left(d\right)={\sum }_{d|n}^{}g\left(\frac{n}{d}\right)$
則有：

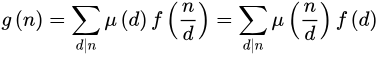
莫比烏斯反演定理證明

參考著個吧
理解就行。重要是定理。(個人認為)

莫比烏斯反演另一性質(與尤拉函數有關)

若n>1且n為正整數，則有${\sum }_{d|n}^{}u\left(d\right)=0$
若n=1，則該式為1、
2，
對任意正整數n均有：

${\sum }_{d|n}^{}\frac{u\left(d\right)}{d}=\frac{\varphi \left(n\right)}{n}$