文章目錄

數位影像處理-DFT&DCT&WHT&小波變換分解重構(Matlab)

數位影像處理-DFT&DCT&WHT&小波變換分解重構(Matlab)

基本的matlab影象處理常式的使用

函數	功能
`imread('影象名')`	讀取影象
`imshow(color_pic)`	顯示影象
`rgb2gray(color_pic)`	將彩色影象轉換成灰度影象
`imhist(gray_pic,n)`	檢視灰度影象的灰度直方圖

程式碼塊

%-----------------Matlab基本影象處理常式使用------------------
clear ;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
figure('name','影象讀取');   
subplot(2,2,1);
imshow(color_pic);   %顯示影象
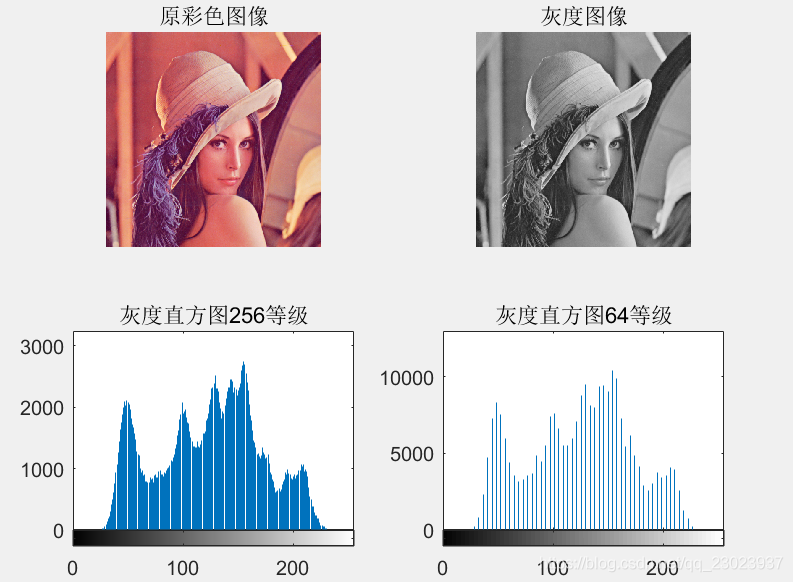
title('原彩色影象');
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
subplot(2,2,2);
imshow(gray_pic);
title('灰度影象');
subplot(2,2,3);
imhist(gray_pic);   %檢視灰度直方圖，預設n=256,256個長度為1的灰度空間
title('灰度直方圖256等級');
subplot(2,2,4);
imhist(gray_pic,64);%n=64，64個長度為4的灰度空間
title('灰度直方圖64等級');

執行效果

在這裡插入圖片描述

傅立葉變換(DFT)

對影象進行傅立葉正變換

%------------------傅立葉變換------------------
clear;  %清除變數
close all; %關閉生成的畫圖視窗
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','傅立葉變換'); %傅立葉變換
subplot(2,2,1);
imshow(gray_pic);
title('原灰度影象');
Fourier=fft2(gray_pic);  %對灰度影象進行傅立葉正變換
log_Fourier=log(abs(Fourier)+1); %取模並進行縮放，調高頻譜影象的低灰度值而對高灰度值僅可能減小
subplot(2,2,2);
imshow(log_Fourier,[]);    %未進行頻譜搬移時的頻譜圖
title('傅立葉變換頻譜圖');
Fourier_shift=fftshift(Fourier); %將頻譜圖中零頻率成分移動至頻譜圖中心
log_Fourier_shift=log(abs(Fourier_shift)+1); %取模並進行縮放，對於（0，1）之間的x值經過取對數後會變成負值，而log（x+1）則將所有的x值對映到正數範圍內
subplot(2,2,3);
imshow(log_Fourier_shift,[]);
title('頻移後的頻譜圖');

程式執行效果：

在這裡插入圖片描述

總結：
在影象的傅立葉頻譜中，原空間域影象上的灰度突變部位、影象結構複雜的區域、影象細節及干擾噪聲等資訊集中在高頻區，原空間域影象上灰度變化平緩部位的資訊(影象輪廓)集中在低頻區。
低頻部分(影象輪廓)對應於未進行頻移的傅立葉頻譜的4個邊角角部分，由於低頻部分能量較集中，因而在頻譜圖上的視覺效果較亮。當進行頻移後，低頻部分移至頻譜中央，中央處最亮。

去除部分高頻分量後對影象進行傅立葉逆變換

%-----------------設定閾值濾除高頻  傅立葉逆變換----------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
threshold=[100000,30000,5000,500];  %設定不同閾值 (高頻部分能量低)
figure('name','傅立葉逆變換影象');
for i=1:4
    Fourier=fft2(gray_pic);  %對灰度影象進行傅立葉正變換
    Fourier_shift=fftshift(Fourier); %將頻譜圖中零頻率成分移動至頻譜圖中心
    h_Fourier_shift=abs(Fourier_shift);% 取傅立葉變換後幅度模值，使灰度值為正數
    Fourier_shift(h_Fourier_shift<threshold(i))=0;  %取閾值消除部分高頻
    IFourier=real(ifft2(ifftshift(Fourier_shift)));  %傅立葉逆變換，要記得先把頻移的頻譜頻移回去
    ret=uint8(IFourier); %將灰度級對映到0-255上
    subplot(2,2,i);
    imshow(ret);
    str=num2str(threshold(i));
    title(['閾值:',str]);
end

程式執行效果：

在這裡插入圖片描述

總結：
因為高頻部分能量較低，即傅立葉變換後的高頻部分幅度值較低，當設定的閾值越小時，保留了更多低頻部分，即輪廓部分保留下來，影象也就恢復的越接近原圖。

離散餘弦變換(DCT)

對影象進行DCT正變換

%----------------DCT變換------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','DCT變換'); 
DCT=dct2(gray_pic);  %DCT變換
h_DCT=abs(DCT);  %DCT變換後的幅度
log_DCT=log(h_DCT);   %%取模並進行縮放，調高頻譜影象的低灰度值而對高灰度值僅可能減小
imshow(log_DCT,[]);
title('DCT變換');
colormap(gray(4));  %重新設定灰度級為4，便於檢視DCT變換後的頻譜圖特點
colorbar;   %顯示顏色欄

程式執行效果：

在這裡插入圖片描述

總結：
從DCT頻譜圖易看出，低頻部分(影象輪廓)能量集中在左上角，因此可進行影象壓縮。

去除部分高頻分量後對影象進行DCT逆變換

%----------------取閾值去除高頻分量 DCT逆變換------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
threshold=[200,100,10,1];  %設定不同閾值 (高頻部分能量低)
for i=1:4
    DCT=dct2(gray_pic); %DCT正變換
    h_DCT=abs(DCT);  %DCT變換後的幅度
    DCT(h_DCT<threshold(i))=0;  %DCT變換後取模得出的幅度值若小於20則至0
    IDCT=uint8(idct2(DCT));  %對影象進行DCT逆變換，並將灰度級對映到0-255上
    subplot(2,2,i);
    imshow(IDCT);
    str=num2str(threshold(i));
    title(['閾值:',str]);
end

程式執行效果：

在這裡插入圖片描述

總結：
因為高頻部分能量較低，即DCT變換後的高頻部分幅度值較低，當設定的閾值越小時，保留了更多低頻部分，即輪廓部分保留下來，影象也就恢復的越接近原圖。

沃爾什哈達瑪變換(WHT)

對影象進行WHT正變換

%------------------沃爾什哈達瑪變換------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','沃爾什哈達瑪'); 
subplot(2,2,1);
imshow(gray_pic);
title('原灰度影象');    %imread讀入源影象為三維，所以不能進行D=A*X*A
im2double_gray_pic=im2double(gray_pic);%必須對讀取的影象做I=im2double(I),函數im2double 將其值歸一化到0～1之間
Hada=hadamard(512); %生成512x512哈達瑪矩陣
Hada_pic=Hada*(im2double_gray_pic)*Hada;
Hada_pic2=Hada_pic/512;  %沃爾什哈達瑪變換記得/(N*N=512*512)，此處只除512是為了頻譜圖效果好看
subplot(2,2,2);
imshow(Hada_pic2);
title('沃爾什哈達瑪變換');

程式執行效果：

在這裡插入圖片描述

去除部分高頻分量後對影象進行WHT逆變換

%----------------取閾值去除高頻分量 沃爾什哈達瑪逆變換------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
im2double_gray_pic=im2double(gray_pic);%必須對讀取的影象做I=im2double(I),函數im2double 將其值歸一化到0～1之間
Hada=hadamard(512);%生成512x512哈達瑪矩陣
Hada_pic=Hada*(im2double_gray_pic)*Hada;
threshold=[0.5,0.3,0.2,0.1];  %設定不同閾值 (高頻部分能量低)
for i=1:4
    Hada_pic2=Hada_pic/(512);  %沃爾什哈達瑪變換記得/(N*N=512*512)，此處只除512是為了頻譜圖效果好看
    h_Hada=abs(Hada_pic2);
    Hada_pic2(h_Hada<threshold(i))=0; %取閾值消除部分高頻
    IHada_pic=Hada'*Hada_pic2*Hada';% Hada'是Hada的轉置矩陣
    IHada_pic2=im2uint8(IHada_pic/512); %將灰度級轉換為255級，否則灰度值大於255，影象太亮，呈現一片白
    subplot(2,2,i);
    imshow(IHada_pic2);
    str=num2str(threshold(i));
    title(['閾值:',str]);
end;

程式執行效果：

在這裡插入圖片描述

總結：
因為高頻部分能量較低，即WHT變換後的高頻部分幅度值較低，當設定的閾值越小時，保留了更多低頻部分，即輪廓部分保留下來，影象也就恢復的越接近原圖。

小波分解重構

一級小波分解

%-------------------小波變換一級分解，小波基函數選db4-----------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','小波變換一級分解');
[c,s]=wavedec2(gray_pic,1,'db4'); %小波一級分解,小波基函數採用db4
ca1=appcoef2(c,s,'db4',1);   %低頻分量
ch1=detcoef2('h',c,s,1);     %高頻水平分量
cv1=detcoef2('v',c,s,1);     %高頻垂直分量
cd1=detcoef2('d',c,s,1);     %高頻對角分量
subplot(2,2,1);imshow(ca1,[]);title('LL1');
subplot(2,2,2);imshow(ch1,[]);title('HL1');
subplot(2,2,3);imshow(cv1,[]);title('LH1');
subplot(2,2,4);imshow(cd1,[]);title('HH1');

程式執行效果：

在這裡插入圖片描述

一級小波重構

%-------------------小波變換一級重構，小波基函數選db4-----------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','小波變換一級重構');
[c,s]=wavedec2(gray_pic,1,'db4'); %小波一級分解,小波基函數採用db4
re_ca1=wrcoef2('a',c,s,'db4',1); %重建第一層低頻分量係數
re_ch1=wrcoef2('h',c,s,'db4',1); %重建第一層高頻水平分量係數
re_cv1=wrcoef2('v',c,s,'db4',1); %重建第一層高頻垂直分量係數
re_cd1=wrcoef2('d',c,s,'db4',1); %重建第一層高頻對角分量係數
re_set1=[re_ca1,re_ch1;re_cv1,re_cd1];  %將各個分量影象拼接在一張影象
subplot(1,2,1);imshow(re_set1,[]);title('第一層小波係數的重構');

re_img1=re_ca1+re_ch1+re_cv1+re_cd1;%將各個分量合併復原
subplot(1,2,2);imshow(re_img1,[]);title('一級重構影象');

程式執行效果：

在這裡插入圖片描述

二級小波分解

%-------------------小波變換二級分解，小波基函數選db4)-----------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','小波變換二級分解');
[c,s]=wavedec2(gray_pic,2,'db4'); %小波二級分解
%小波一級分解分量
ca1=appcoef2(c,s,'db4',1);   %低頻分量
ch1=detcoef2('h',c,s,1);     %高頻水平分量
cv1=detcoef2('v',c,s,1);     %高頻垂直分量
cd1=detcoef2('d',c,s,1);     %高頻對角分量
%顯示第1級分解各分量
subplot(4,4,[3,4,7,8]);imshow(ch1,[]);title('HL1');
subplot(4,4,[9,10,13,14]);imshow(cv1,[]);title('LH1');
subplot(4,4,[11,12,15,16]);imshow(cd1,[]);title('HH1');
% %提取第2層的各分量
ca2=appcoef2(c,s,'db4',2);   %低頻分量
ch2=detcoef2('h',c,s,2);     %高頻水平分量
cv2=detcoef2('v',c,s,2);     %高頻垂直分量
cd2=detcoef2('d',c,s,2);     %高頻對角分量
% %顯示第2級分解各分量
subplot(4,4,1);imshow(ca2,[]);title('LL2');
subplot(4,4,2);imshow(ch2,[]);title('HL2');
subplot(4,4,5);imshow(cv2,[]);title('LH2');
subplot(4,4,6);imshow(cd2,[]);title('HH2');

程式執行效果：

在這裡插入圖片描述

二級小波重構

%-------------------小波變換2級重構，小波基函數選db4-----------------------
clear;
close all;
color_pic=imread('lena512color.bmp');  %讀取影象
gray_pic=rgb2gray(color_pic);  %將彩色圖轉換成灰度圖
figure('name','小波變換二級重構');
[c,s]=wavedec2(gray_pic,2,'db4'); %小波二級分解
re_ca2=wrcoef2('a',c,s,'db4',2);  %重建第二層低頻分量係數
re_ch2=wrcoef2('h',c,s,'db4',2);  %重建第二層高頻水平分量係數
re_cv2=wrcoef2('v',c,s,'db4',2);  %重建第二層高頻垂直分量係數
re_cd2=wrcoef2('d',c,s,'db4',2);  %重建第二層高頻對角分量係數
re_set2=[re_ca2,re_ch2;re_cv2,re_cd2]; %將各個分量影象拼接在一張影象
subplot(1,2,1);imshow(re_set2,[]);title('第二層小波係數的重構');
re_img2=re_ca2+re_ch2+re_cv2+re_cd2; %將各個分量合併復原
subplot(1,2,2);imshow(re_img2,[]);title('二級重構影象');

程式執行效果：

在這裡插入圖片描述