揹包

【揹包】
今天來講講揹包問題
揹包問題是DP問題的一種。
而DP問題離不開三個特性：

1. 最優子結構
2. 無後效性
3. 重疊子問題

在講揹包問題之前，我們先講講斐波那契數列。
總所周知斐波那契數列的遞推公式是
F(n)=F(n-1)+F(n-2)
但是我們可以畫個圖看看，在使用遞迴求解斐波那契數列第N項的時候會發生什麼問題

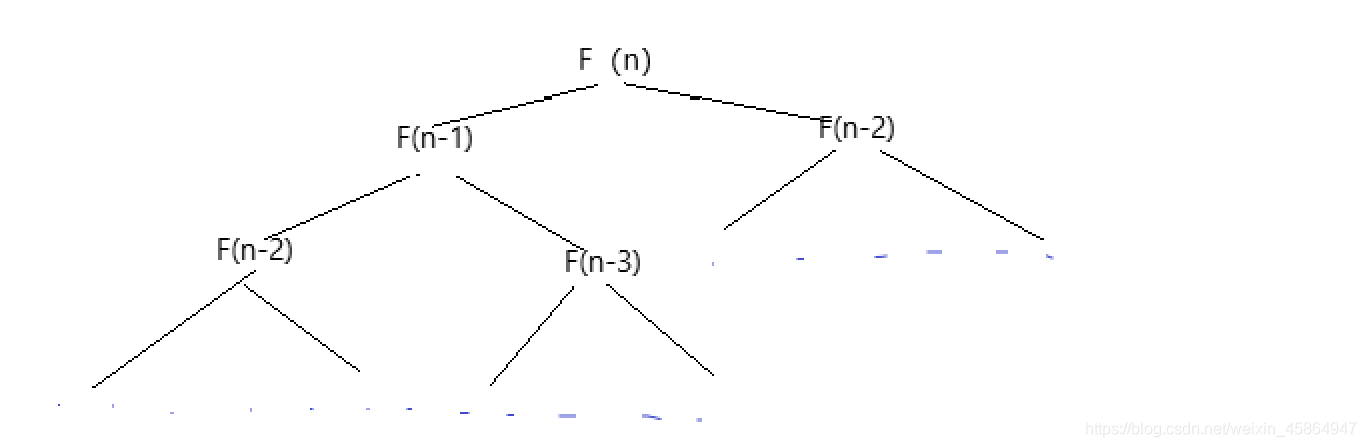
寫到這裡應該就很清楚了。我們要求F（n）一定要遞迴求得F（n-1）和F（n-2），但是我們在求F（n-1）的時候，我還需要再遞迴求一個F（n-2），那麼時間的開銷就變大了許多許多。這就是上面DP說的重疊子問題，我重複地求了一個值，以至於當n很大很大地時候接近葉子節點地上一層地資料被計算了相當多次，這時間地開銷是非常非常大的。而且我們從時間複雜度的角度出發，這個演演算法本身也是O(2^n)。
那麼。我們從節省時間的角度我們去解決一下斐波那契數列。既然我們重複地計算了某一個值，那我們能不能用一個變數先存放他在那。直到用的時候，我才把他排程出來。也就是說，我們從n=2開始我們用for迴圈遞進的方式，一個一個地求出前n-1項地值，那麼我們在計算第n項地值得時候，我們就可以之間從陣列中通過下標索引得方式去得到F（n-1）和F（n-2）從而計算出F（n）的值。
這裡我就不進行程式碼實現了。
我們迴歸到今天的主角：揹包問題
有N件物品和一個容量為V的揹包。每種物品均只有一件。 第i件物品的品質是w[i]，價值是c[i]。求解將哪些物品裝入揹包可使這些物品的品質總和不超過揹包容量，且價值總和最大。
在本題中，乍一看，好像沒有思路，或者有的同學會覺得價效比方案可以解決揹包問題
我們一步步來仿照剛剛的斐波那契數列的O（n）求解法

第一步

我們先完成簡單的輸入，把緩衝區的資料全部讀進一個陣列中，並按照價值，升序排序

struct object {
	int val;
	int weight;
};

//這裡是儲存的資料型別

int main() {
	int T;
	//T代表著我有多少個物體

	while (cin >> T) {
		int weight = 0;
		cin >> weight;
		object* Arr = new object[T];
		for (int count = 0; count < T; count++) cin >> Arr[count].val >> Arr[count].weight;
		//input
		//sort
		for (int count = 0; count < T; count++) {
			for (int j = count+1; j < T; j++) {
				if (Arr[count].val > Arr[j].val) {
					//change
					object tem = Arr[count];
					Arr[count] = Arr[j];
					Arr[j] = tem;
				}
			}
		}
	}
}

這裡用了氣泡排序增強可讀性，我們也可以用其他更快速的排序去減少時間的複雜度，不過這不屬於我們的核心程式碼塊
我們這裡直接定義一個函數名為DP_bag
圖解如下

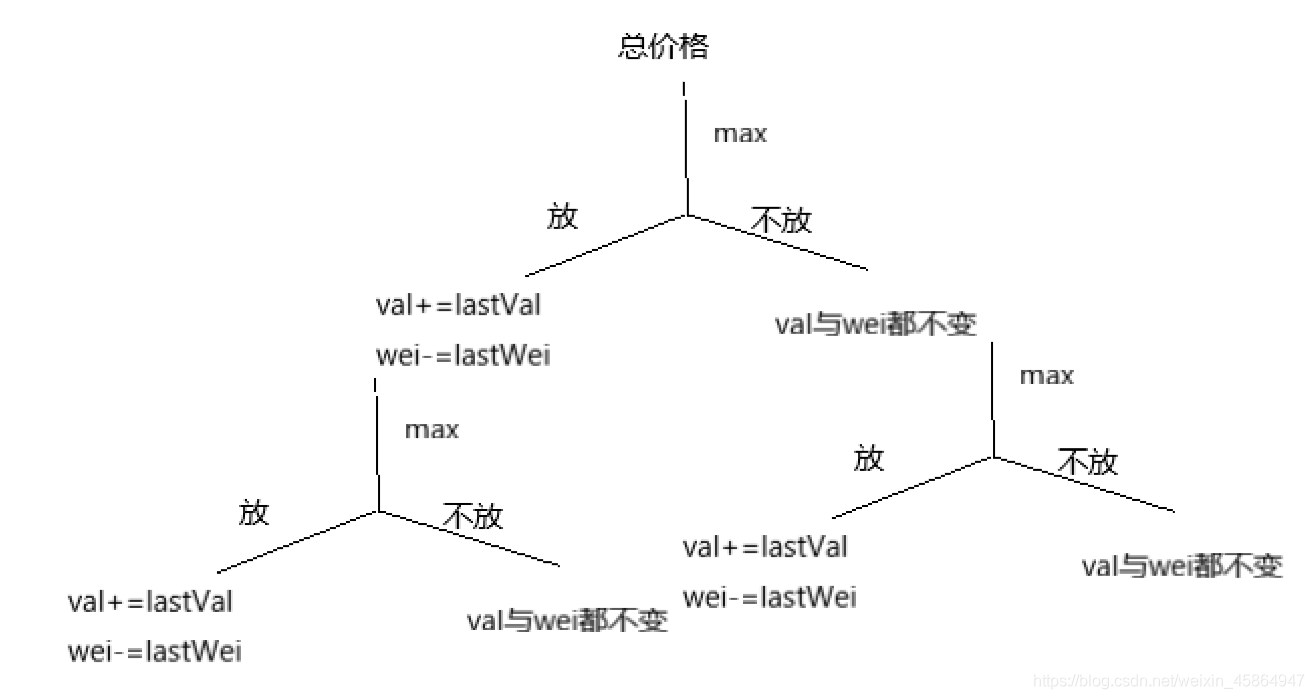
於是我們便有遞迴實現的程式碼

int DP_bag(object *Arr,int Value,int weight,int last){
	
	if (last < 0)return 0;//裝不下了
	else if (weight < Arr[last].weight)return DP_bag(Arr, Value, weight, last - 1);//裝不下最貴的，往後找
	else return max(DP_bag(Arr, Value, weight, last - 1), Arr[last].val +DP_bag(Arr, Arr[last].val + Value, weight - Arr[last].weight, last - 1));	
}

找到最優子結構和重疊子問題後就可轉換
有空再更，困了