「王曉東」 版DP經典習題總結&AC程式碼(C++)
最小m段和問題
【問題描述】
給定 n 個整陣列成的序列,現在要求將序列分割為 m 段,每段子序列中的數在原序列
中連續排列。如何分割才能使這 m段子序列的和的最大值達到最小?
演演算法設計:
給定 n 個整陣列成的序列,計算該序列的最優 m段分割,使 m段子序列的和的最大值達到最小。
【輸入形式】
輸入資料:第 1 行中有 2 個正整數 n 和 m。正整數 n 是序列的長度;正整數 m是分割的段數。接下來的一行中有 n 個整數。
【輸出形式】
將計算結果輸出:第 1 行中的數是計算出的 m段子序列的和的最大值的最小值。
【樣例輸入】
1 1
10
【樣例輸出】
10
/*
--------------------------------------
--------------------------------------
------Problem: 8918.最小m段和問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int n,m,a[1005];
int dp[1005][1005];
int sum[1005][1005];
int main()
{
cin >> n >> m;
for(int i=1; i<=n; i++) cin >> a[i];
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
dp[i][j] = 1000000000;
for(int i=1; i<=n; i++) {
int num = 0;
for(int j=i; j<=n; j++) {
num += a[j];
sum[i][j] = num;
}
dp[i][1] = sum[1][i];
}
for(int i=2; i<=n; i++) {
for(int j=2; j<=i && j<=m; j++) {
int p;
for(int k=1; k<i; k++)
dp[i][j] = min(dp[i][j], max(dp[k][j - 1], sum[k + 1][i]));
}
}
cout << dp[n][m] << endl;
return 0;
}
最大 k 乘積問題
【問題描述】
設 I 是一個 n 位十進位制整數。如果將 I 劃分為 k 段,則可得到 k 個整數。這 k 個整數的
乘積稱為 I 的一個 k 乘積。試設計一個演演算法,對於給定的 I 和 k,求出 I 的最大 k 乘積。
演演算法設計:
對於給定的 I 和 k,計算 I 的最大 k 乘積。
【輸入形式】
輸入資料:第 1 行中有 2 個正整數 n 和 k。正整數 n 是序列
的長度;正整數 k 是分割的段數。
接下來的一行中是一個 n 位十進位制整數。(n<=10)
【輸出形式】
將計算結果輸出:第 1 行中的數是計算出的最大 k 乘積。
【樣例輸入】
2 1
15
【樣例輸出】
15
/*
--------------------------------------
--------------------------------------
-------Problem: 8917.最大k乘積問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
int dp[15][15]; //最大乘積陣列
char numstr[15];
int num[15];
int getValue(int i,int j) {
int sum = 0;
for(int k=i; k<j; k++) {
sum += num[k];
sum *= 10;
}
return sum + num[j];
}
void dpAlgo(int l,int k) {
for(int i=1; i<=l; i++)
dp[i][1] = getValue(1,i);
for(int i=0; i<=l; i++) {
for(int j=2; j<=k; j++) {
int temp = 0;
for(int d=1; d<i; d++)
temp = max(temp,dp[d][j-1] * getValue(d+1,i));
dp[i][j] = temp;
}
}
}
int main()
{
int l,k;
cin>>l>>k>>numstr;
for(int i=0; i<l; i++)
num[i+1] = numstr[i] - '0';
dpAlgo(l,k);
cout << dp[l][k];
return 0;
}
石子合併問題
【問題描述】
在一個圓形操場的四周擺放著 n 堆石子。現要將石子有次序地合併成一堆。規定每次只能選相鄰的 2 堆石子合併成新的一堆,並將新的一堆石子數記為該次合併的得分。試設計一個演演算法,計算出將 n 堆石子合併成一堆的最小得分和最大得分。
演演算法設計:
對於給定 n 堆石子,計算合併成一堆的最小得分和最大得分。
【輸入形式】
輸入資料:第 1 行是正整數 n,1≤n≤100,表示有 n 堆石子。
第二行有 n 個數,分別表示每堆石子的個數。
【輸出形式】
將計算結果輸出:第 1 行中的數是最小得分;第 2 行中的數是最大得分。
【樣例輸入】
4
4 4 5 9
【樣例輸出】
43
54
/*
--------------------------------------
--------------------------------------
--------Problem: 8920.石子合併問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
const int INF=0x7fffffff;
int n,m,ans1,ans2;
int A[205],f1[205][205],f2[205][205];
int dfs1(int L,int R){ //求出最小得分
if(f1[L][R])return f1[L][R]; //已儲存的狀態不必搜尋
if(L==R) return f1[L][R]=0; //L==R時返回0
int res=INF; //初始值賦為最大值以求最小值
for(int k=L;k<R;k++) //列舉K搜尋
res=min(res,dfs1(L,k)+dfs1(k+1,R)+A[R]-A[L-1]);
return f1[L][R]=res; //記錄狀態
}
int dfs2(int L,int R){ //求出最大得分
if(f2[L][R])return f2[L][R];
if(L==R) return f2[L][R]=0; //若初始值為0可省略該句
int res=0; //初始值設為0
for(int k=L;k<R;k++)
res=max(res,dfs2(L,k)+dfs2(k+1,R)+A[R]-A[L-1]);
return f2[L][R]=res;
}
int main(){
std::ios::sync_with_stdio(false);//取消cin與stdin同步,加速讀入
cin>>n;
for(int i=1;i<=n;i++){
cin>>A[i];
A[i+n]=A[i]; //因為是環所以儲存為長度為2n的鏈以保證不會漏解
}
for(int i=1;i<=2*n;i++) //求出字首和
A[i]+=A[i-1];
dfs1(1,2*n);dfs2(1,2*n); //搜尋出1-2n的最大得分與最小得分
ans1=INF; ans2=0;
for(int i=1;i<=n;i++){
ans1=min(f1[i][n+i-1],ans1);//選出答案
ans2=max(f2[i][n+i-1],ans2);
}
cout<<ans1<<"\n"<<ans2;
return 0;
}
最大長方體問題
【問題描述】
一個長,寬,高分別為 m,n,p 的長方體被分割成個 mnp 個小立方體。每個小立方體內有一個整數。試設計一個演演算法,計算出所給長方體的最大子長方體。子長方體的大小由它所含所有整數之和確定。
演演算法設計:
對於給定的長,寬,高分別為 m,n,p 的長方體,計算最大子長方體的大小。
【輸入形式】
輸入資料:第 1 行是 3 個正整數 m,n,p,1≤m,n,p≤50。接下來 m*n 行每行 p 個正整數,表示小立方體中的數。
【輸出形式】
將計算結果輸出:第 1 行中的數是計算出的最大子長方體的大小。
【樣例輸入】
3 3 3
0 -1 2
1 2 2
1 1 -2
-2 -1 -1
-3 3 -2
-2 -3 1
-2 3 3
0 1 3
2 1 -3
【樣例輸出】
14
/*
--------------------------------------
--------------------------------------
-------Problem: 8916.最大長方體問題---
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
int maxsum(int n,int *a)
{
int sum=0,b=0;
for (int i=1; i<=n; i++)
{
if(b>0) b+=a[i];
else b=a[i];
if(b>sum) sum=b;//記錄最大值
}
return sum;
}
int maxsum2(int m,int n, int **a){
int sum=0;
int *b=new int [n+1];
for (int i=1; i<=m; i++) {
for(int k=1; k<=n; k++)
b[k]=0;//置0
for(int j=i; j<=m; j++) {//動規思想,將m分成1~i和i+1~m兩段
for (int k=1; k<=n; k++)
b[k] += a[j][k];
int max=maxsum(n,b);
if(max>sum) sum=max;
}
}
return sum;
}
int maxsum3(int m,int n,int p,int ***a)
{
int sum=0;
int **c=new int*[n+1];
for(int i=1; i<=n; i++) c[i]=new int [p+1];
for(int i=1; i<=m; i++)
{
for(int j=1; j<=n; j++)
for(int k=1; k<=p ; k++) c[j][k]=0;//置0
for (int l=i; l<=m; l++) {//和二維的思想一樣
for(int j=1; j<=n; j++)
for(int k=1; k<=p ; k++) c[j][k]+=a[l][j][k];
int max=maxsum2(n,p,c);
if(max>sum) sum=max;
}
}
return sum;
}
int main()
{
int m,n,p,***a;
cin>>m>>n>>p;
a=new int**[m+1];
for(int i=1; i<=m; i++) a[i]=new int*[n+1]; //一維
for(int i=1; i<=m; i++)
for (int j=1; j<=n; j++)
a[i][j]=new int[p+1]; //二維
for(int i=1; i<=m; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=p; k++)
cin>>a[i][j][k]; //三維
cout<<maxsum3(m,n,p,a);
}
序關係計數問題
【問題描述】
用關係「<」和「=」將 3 個數 A、B 和 C 依序排列時有 13 種不同的序關係:A=B=C,A=B<C,A<B=C,A<B<C,A<C<B,A=C<B,B<A=C,B<A<C,B<C<A,B=C<A,C<A=B,C<A<B,C<B<A。將n 個數(1 ≤ n ≤50)依序排列時有多少種序關係。
演演算法設計:
計算出將n 個數(1 ≤ n ≤50)依序排列時有多少種序關係。
【輸入形式】
輸入資料:輸入資料有多行,每行提供一個數n 。
【輸出形式】
將找到的序關係數輸出:一行一個。
【樣例輸入】
3
5
【樣例輸出】
13
541
/*
--------------------------------------
--------------------------------------
-------Problem: 8923.序關係計數問題---
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
#define MAX_N 51
using namespace std;
__int64 dp[MAX_N][MAX_N]; //dp[i][j]:i個數,有j個‘<’連結,共有多少種情況
int main()
{
int n,i,j;
for(i=0; i<MAX_N; i++) dp[i][0]=1;
for(i=0; i<MAX_N; i++)
for(j=1; j<i; j++)
dp[i][j] = (j+1)*(dp[i-1][j]+dp[i-1][j-1]);
for(i=0; i<MAX_N; i++)
for(j=0; j<i; j++)
dp[i][i] += dp[i][j]; //dp[i][i]存放每一行的和
while(scanf("%d",&n)==1){
printf("%I64d\n",dp[n][n]);
}
return 0;
}
汽車加油行駛問題
【問題描述】
給定一個N*N 的方形網格,設其左上角為起點,座標為(1,1),X 軸向右為正,Y 軸向下為正,每個方格邊長為1。一輛汽車從起點出發駛向右下角終點,其座標為(N,N)。在若干個網格交叉點處,設定了油庫,可供汽車在行駛途中加油。汽車在行駛過程中應遵守
如下規則:(1)汽車只能沿網格邊行駛,裝滿油後能行駛K 條網格邊。出發時汽車已裝滿油,在起點與終點處不設油庫。(2)當汽車行駛經過一條網格邊時,若其 X 座標或 Y 座標減小,則應付費用B,否則免付費用。(3)汽車在行駛過程中遇油庫則應加滿油並付加油費用A。(4)在需要時可在網格點處增設油庫,並付增設油庫費用C(不含加油費用A)。(5)(1)~(4)中的各數N、K、A、B、C均為正整數。
演演算法設計:
求汽車從起點出發到達終點的一條所付費用最少的行駛路線。
【輸入形式】
輸入資料:
第一行是N,K,A,B,C的值,2 ≤ N ≤ 100,2 ≤ K ≤ 10。第二行起是一個N*N 的0-1方陣,每行N 個值,至N+1行結束。方陣的第i行第j 列處的值為1 表示在網格交叉點(i,j)處設定了一個油庫,為0 時表示未設油庫。各行相鄰的2 個數以空格分隔。
【輸出形式】
將找到的最優行駛路線所需的費用,即最小費用輸出:第1行中的數是最小費用值。
【樣例輸入】
9 3 2 3 6
0 0 0 0 1 0 0 0 0
0 0 0 1 0 1 1 0 0
1 0 1 0 0 0 0 1 0
0 0 0 0 0 1 0 0 1
1 0 0 1 0 0 1 0 0
0 1 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0 1
1 0 0 1 0 0 0 1 0
0 1 0 0 0 0 0 0 0
【樣例輸出】
12
/*
--------------------------------------
--------------------------------------
-----Problem: 8910.汽車加油行駛問題---
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include<bits/stdc++.h>
#include<set>
#include<map>
using namespace std;
#define MAX 120
inline int read()
{
int x=0,t=1;char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')t=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
return x*t;
}
struct Line
{
int v,next,w;
}e[MAX*MAX*MAX];
int h[MAX*MAX],cnt=1,tot;
int m[MAX*MAX],g[MAX][MAX],n,K,A,B,C;
bool vis[MAX*MAX][15];
inline void Add(int u,int v,int w)
{
e[cnt]=(Line){v,h[u],w};h[u]=cnt++;
}
int dis[MAX*MAX][15];
void SPFA()
{
memset(dis,63,sizeof(dis));
dis[g[1][1]][K]=0;
queue<int> Q,Q1;
Q.push(g[1][1]);Q1.push(K);
while(!Q.empty())
{
int u=Q.front(),t=Q1.front();
Q.pop();Q1.pop();
if(t!=0)
{
for(int i=h[u];i;i=e[i].next)
{
int v=e[i].v,gg=t-1,Dis=dis[u][t]+e[i].w;
if(m[v])gg=K,Dis+=A;
if(dis[v][gg]>Dis)
{
dis[v][gg]=Dis;
if(!vis[v][gg])vis[v][gg]=true,Q.push(v),Q1.push(gg);
}
}
}
int v=u,gg=K,Dis=dis[u][t]+C+A;
if(dis[v][gg]>Dis)
{
dis[v][gg]=Dis;
if(!vis[v][gg])vis[v][gg]=true,Q.push(v),Q1.push(gg);
}
vis[u][t]=false;
}
}
int main()
{
n=read();K=read();A=read();B=read();C=read();
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
g[i][j]=++tot,m[g[i][j]]=read();;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
{
if(i!=n) Add(g[i][j],g[i+1][j],0);
if(j!=n) Add(g[i][j],g[i][j+1],0);
if(i!=1) Add(g[i][j],g[i-1][j],B);
if(j!=1) Add(g[i][j],g[i][j-1],B);
}
SPFA();
int ans=1e9;
for(int i=0;i<=K;++i)ans=min(ans,dis[g[n][n]][i]);
printf("%d\n",ans);
return 0;
}
最少硬幣問題
【問題描述】
設有 n 種不同面值的硬幣,各硬幣的面值存於陣列 T[1:n]中。現要用這些面值的硬幣來找錢。可以使用的各種面值的硬幣個數存於陣列 Coins[1:n]中。對任意錢數 0≤m≤20001,設計一個用最少硬幣找錢 m 的方法。
演演算法設計:
對於給定的 1≤n≤10,硬幣面值陣列 T 和可以使用的各種面值的硬幣個數陣列 Coins,以及錢數 m,0≤m≤20001,計算找錢 m的最少硬幣數。
【輸入形式】
輸入資料:第一行中只有 1 個整數給出n 的值,第 2 行起每
行 2 個數,分別是 T[j]和 Coins[j]。最後 1 行是要找的錢數 m。
【輸出形式】
將計算出的最少硬幣數輸出。問題無解時輸出-1。
【樣例輸入】
3
1 3
2 3
5 3
18
【樣例輸出】
5
/*
--------------------------------------
--------------------------------------
--------Problem: 8913.最少硬幣問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
/*多重揹包(硬幣種類有限制,硬幣數目有限制)*/
#include <iostream>
using namespace std;
const int maxvalue = 20001;
const int coinnum = 15;
int mymin(int a,int b){
return a < b ? a : b;
}
int main()
{
int n;
cin >> n;
int coin[coinnum];
int coincount[coinnum];
for(int i=0; i<n; i++)
{
cin >> coin[i];
cin >> coincount[i];
}
int m;
cin >> m;
//錢數為dp[i]是的硬幣數目
int *dp = new int[maxvalue]();
//重點錯誤
//for(int i=0; i<=m; i++)是錯的
for(int i=1; i<=m; i++) dp[i] = maxvalue;
int i,j,k;
for(i=0; i<n; i++)//硬幣面值的種數
{
for(j=1; j<=coincount[i]; j++)//硬幣的面值的個數
{
for(k=m; k>=coin[i]; k--) //動態遷移方程為
dp[k] = mymin(dp[k - coin[i]] + 1, dp[k]);
}
}
if(dp[m] == maxvalue)
cout << -1 << endl;
else cout << dp[m] << endl;
return 0;
}
租用遊艇問題
【問題描述】
長江遊艇俱樂部在長江上設定了 n 個遊艇出租站 1,2,…,n。遊客可在這些遊艇出租站租用遊艇,並在下游的任何一個遊艇出租站歸還遊艇。遊艇出租站 i 到遊艇出租站 j 之間的租金為 r(i,j),1≤i<j≤n。試設計一個演演算法,計算出從遊艇出租站 1 到遊艇出租站 n 所需的最少租金。
演演算法設計:
對於給定的遊艇出租站 i 到遊艇出租站 j 之間的租金為 r(i,j),1≤i<j≤n,計算從遊艇出租站 1 到遊艇出租站 n 所需的最少租金。
【輸入形式】
輸入資料:第 1 行中有 1 個正整數 n(n<=200),表示有 n個遊艇出租站。接下來的 n-1 行是 r(i,j),1≤i<j≤n。
【輸出形式】
將計算出的從遊艇出租站 1 到遊艇出租站 n 所需的最少租金輸出。
【樣例輸入】
3
5 15
7
【樣例輸出】
12
/*
--------------------------------------
--------------------------------------
--------Problem: 8924.租用遊艇問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include<bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
int n,v[222][222];
int dp[222];//dp[i]表示到第i個遊艇出租站所需的最少租金
int main()
{
scanf("%d",&n);
for(int i=1; i<n; i++)
for(int j=i+1; j<=n; j++)
scanf("%d",&v[i][j]);
memset(dp,INF,sizeof(dp));
dp[1]=0;
for(int i=2; i<=n; i++)
for(int j=1; j<i; j++)
dp[i] = min(dp[i],dp[j]+v[j][i]);
printf("%d\n",dp[n]);
return 0;
}
紅黑樹的紅色內結點問題
【問題描述】
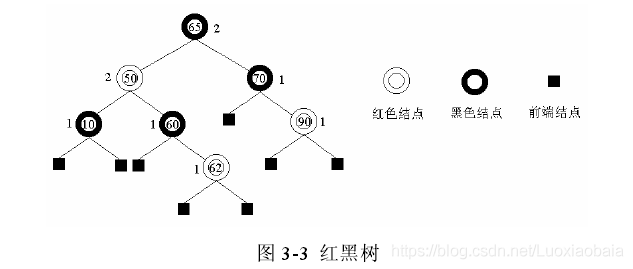
紅黑樹是一類特殊的二元搜尋樹,其中每個結點被「染成」紅色或黑色。若將二元搜尋樹結點中的空指標看作是指向一個空結點,則稱這類空結點為二元搜尋樹的前端結點。並規定所有前端結點的高度為-1。
一棵紅黑樹是滿足下面「紅黑性質」染色二元搜尋樹:
(1)每個結點被染成紅色或黑色;
(2)每個前端結點為黑色結點;
(3)任一紅結點的兒子結點均為黑結點;
(4)在從任一結點到其子孫前端結點的所有路徑上具有相同的黑結點數。
從紅黑樹中任一結點 x 出發(不包括結點 x),到達一個前端結點的任意一條路徑上的黑結點個數稱為結點 x 的黑高度,記作 bh(x)。紅黑樹的黑高度定義為其根結點的黑高度。圖示的二元搜尋樹是一棵紅黑樹。標在結點旁邊的數位是相應結點的黑高度。
演演算法設計:
給定正整數 n,試設計一個演演算法,計算出在所有含有 n 個結點的紅黑樹中,紅色內結點個數的最小值和最大值。
【輸入形式】
輸入資料:第一行是正整數 n,1<n<5000。
【輸出形式】
將紅色內結點個數的最小值和最大值輸出:第 1 行是最小值,第 2行是最大值。
【樣例輸入】
8
【樣例輸出】
1
4
/*
--------------------------------------
--------------------------------------
------8830. 紅黑樹的紅色內結點問題----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
int n,m,ans;
int main()
{
scanf("%d",&n);
m=n+1;
while(m>1) {
ans+=m&1;m>>=1;
}
printf("%d\n",ans);
m=n+1;ans=0;
while(m>1)
{
if(m==2) ans++;
if((m&3)==1) ans+=m/4*2-1,m/=4,m++;
else if((m&3)==2) ans+=m/4*2,m/=4,m++;
else if((m&3)==3) ans+=m/4*2+1,m/=4,m++;
else ans+=m/4*2,m/=4;
}
printf("%d\n",ans);
return 0;
}
編輯距離問題
【問題描述】
設 A 和 B 是 2 個字串。要用最少的字元操作將字串 A 轉換為字串 B。這裡所說的字元操作包括
(1)刪除一個字元;
(2)插入一個字元;
(3)將一個字元改為另一個字元。
將字串 A 變換為字串 B 所用的最少字元運算元稱為字串 A 到 B 的編輯距離,記為d(A,B)。試設計一個有效演演算法,對任給的2個字串A和B,計算出它們的編輯距離d(A,B)。
演演算法設計:
對於給定的字串 A 和字串 B,計算其編輯距離 d(A,B)。
【輸入形式】
輸入資料:第一行是字串 A,檔案的第二行是字串 B。
【輸出形式】
將編輯距離 d(A,B)輸出到第 1 行中。
【樣例輸入】
fxpimu
xwrs
【樣例輸出】
5
/*
--------------------------------------
--------------------------------------
---------------8829. 編輯距離問題-----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
int d[2005][2005];
/*
輸入的兩個字元陣列為a[], b[],從下標為0開始初始化
長度分別為length_a, length_b
陣列d[m][n]存放從a[1:m] 變為 b[1:n]所需要的最少操作
遞迴公式:
d[i][j] = 0, i=0或j=0 時(即陣列的第一行和第一列均為0)
1<=i<=length_a, 1<=j<=length_b
d[i][j] = d[i-1][j-1], a[i-1] == b[j-1]
d[i][j] = min(d[i-1][j-1]+1, d[i][j-1]+1, d[i-1][j]+1), a[i-1] != b[j-1]
最優值:d[length_a][length_b]
*/
int min(int a, int b, int c)
{
int temp = a;
if(temp>b) temp = b;
if(temp>c) temp =c;
return temp;
}
int edit(char *a, char *b)
{
int length_a = strlen(a);
int length_b = strlen(b);
for(int i=0; i<=length_a; i++) d[i][0] = i;
for(int i=0; i<=length_b; i++) d[0][i] = i;
for(int i=1; i<=length_a; i++) {
for(int j=1; j<=length_b; j++) {
if(a[i-1] == b[j-1])
d[i][j] = min(d[i-1][j-1], d[i][j-1]+1, d[i-1][j]+1);
else
d[i][j] = min(d[i-1][j-1]+1, d[i][j-1]+1, d[i-1][j]+1);
}
}
return d[length_a][length_b];
}
int main()
{
char a[2000], b[2000];
cin>>a>>b;
cout<<edit(a,b);
}
圈乘運算問題
【問題描述】
關於整數的 2 元圈乘運算⊗定義為(X⊗Y)=10 進位制整數 X 的各位數位之和 * 10 進位制整數 Y 的最大數位+Y 的最小數位。例如,(9⊗30)=9*3+0=27。對於給定的 10 進位制整數 X 和 K,由 X 和⊗運算可以組成各種不同的表示式。試設計一個演演算法,計算出由 X 和⊗運算組成的值為 K 的表示式最少需用多少個⊗運算。
演演算法設計:
給定 10 進位制整數 X 和 K (1≤X,K≤1020) 。計算由 X 和⊗運算組成的值為 K 的表示式最少需用多少個⊗運算。
【輸入形式】
輸入資料:每一行有 2 個 10 進位制整數 X 和 K。最後一行是 0 0(以0 0結束)。
【輸出形式】
將找到的最少⊗運算個數輸出。
【樣例輸入】
3 12
0 0
【樣例輸出】
1
這題TLE了,明天藍橋,之後AC了再補上
/*
--------------------------------------
--------------------------------------
---------------8911. 圈乘運算問題-----
--------------------------------------
----------------------Author----------
--------------------------------------
----------------------XZITXX----------
--------------------------------------
*/
#include <bits/stdc++.h>
using namespace std;
const int MAX=81*30+9,MIN=-1;
int NumLen(int x){//統計位數
int len = 0;
while (x>0){
len++;
x /= 10;
}
return len;
}
void Init(int* a, int x){//作初始化
int min = 10;
int max = 0;
int num = 0;
int tend = 0;
while (x > 0){
tend = x % 10;
x /= 10;
num += tend;
if (tend > max){
max = tend;
}
if (tend < min){
min = tend;
}
}
a[0] = MAX;//存放最小圈乘次數
a[1] = num;//存放各位數之和
a[2] = min;//存放最小的數
a[3] = max;//存放最大的數
}
int main()
{
int x,k;
while(~scanf("%d%d",&x,&k)&&x!=0&&k!=0)
{
int n = NumLen(x);//表示x的位數
int m = 81*n+9;//b最小可以2為陣列合,最大為9,最小為9.所以(x的各位數相加)*9+9;x的各位數相加最大為9*n;
if(m<177){//因為y可能是2位數,導致1位數的x圈乘後的結果為2位數
m = 177;
}
if (k>m){//若k大於x的最大圈乘數則退出
return -1;
}
int** r = new int*[m+2];//建立二維陣列
for (int i=0; i<m+1; i++){//遍歷每
r[i] = new int[4];
Init(r[i],i);
}
r[m+1] = new int[4];
Init(r[m+1], x);//將起始x寫到陣列的最後
r[m+1][0] = 0;//變成自己不需要圈乘
//開始操作
int flag = 1;
while (flag){//不斷在序列中更新
flag = 0;
for (int i=1; i<=m+1; i++){//尋找X
if (r[i][0] < MAX){
for (int j=1; j<=m+1; j++){//尋找Y
if (r[j][0] < MAX){
int tend = r[i][1] * r[j][3] + r[j][2];//計算圈乘結果
if (r[tend][0]>r[i][0]+r[j][0]+1){//與原來的圈乘生產該數的次數對比找最小
flag = 1;//若有變化則更新x的尋值
r[tend][0] = r[i][0] + r[j][0] + 1; //r[i][0]為得到x的圈乘次數,r[j][0]位得到y的圈乘次數
}//endif
}//endif
}
}//endif
}
}
cout << r[k][0] << endl;
}
return 0;
}