---

前言

貝葉斯網路又稱信度網路，是Bayes方法的擴充套件，是目前不確定知識表達和推理領域最有效的理論模型之一。從1988年由Pearl提出後，已經成為近幾年來研究的熱點.。一個貝葉斯網路是一個有向無環圖(Directed Acyclic Graph,DAG),由代表變數節點及連線這些節點有向邊構成。節點代表隨機變數，節點間的有向邊代表了節點間的互相關係(由父節點指向其子節點)，用條件概率進行表達關係強度，沒有父節點的用先驗概率進行資訊表達。節點變數可以是任何問題的抽象，如：測試值，觀測現象，意見徵詢等。適用於表達和分析不確定性和概率性的事件，應用於有條件地依賴多種控制因素的決策，可以從不完全、不精確或不確定的知識或資訊中做出推理。
本文是對草地溼模型進行研究。

一、草地溼模型

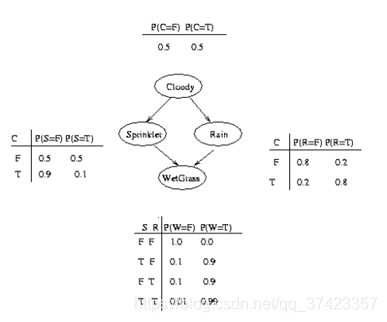
貝葉斯結構圖：

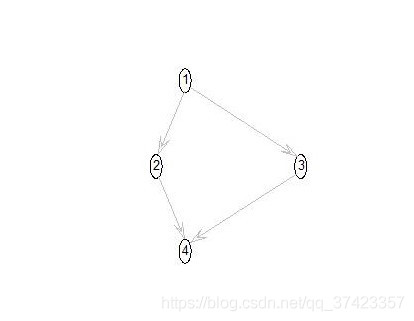
二、BNT引數學習(MATLAB)

程式碼如下（範例）：

#模型設定#

N=4;
dag=zeros(N,N);
C=1;S=2;R=3;W=4;
dag(C,[R S])=1;
dag(R,W)=1;
dag(S,W)=1;

#生成多項式條件概率#

false = 1; true = 2;
ns = 2*ones(1,N); % binary nodes 節點狀態數
figure
draw_graph(dag);
bnet = mk_bnet(dag, ns);
bnet.CPD{C} = tabular_CPD(bnet, C, [0.5 0.5]);
bnet.CPD{R} = tabular_CPD(bnet, R, [0.8 0.2 0.2 0.8]);
bnet.CPD{S} = tabular_CPD(bnet, S, [0.5 0.9 0.5 0.1]);
bnet.CPD{W} = tabular_CPD(bnet, W, [1 0.1 0.1 0.01 0 0.9 0.9 0.99]);

bnet.CPD{W}

CPT = cell(1,N);
for i=1:N
  s=struct(bnet.CPD{i});  % 建立或轉換為結構陣列。
  CPT{i}=s.CPT;
end

#構造樣本資料#

nsamples =5000;
samples = cell(N, nsamples); %建立單元格陣列

for i=1:nsamples
  samples(:,i) = sample_bnet(bnet); %SAMPLE_BNET從貝葉斯網路生成隨機樣本。
end
data = cell2num(samples); %CELL2NUM將2D單元格陣列轉換為2D數位陣列

#建立貝葉斯網路#

bnet2 = mk_bnet(dag, ns);  

#手動構造條件概率表cpt#

bnet2.CPD{C} = tabular_CPD(bnet2, C, 'clamped', 1, 'CPT', [0.5 0.5], ...
			   'prior_type', 'dirichlet', 'dirichlet_weight', 0);
bnet2.CPD{R} = tabular_CPD(bnet2, R, 'prior_type', 'dirichlet', 'dirichlet_weight', 0);
bnet2.CPD{S} = tabular_CPD(bnet2, S, 'prior_type', 'dirichlet', 'dirichlet_weight', 0);
bnet2.CPD{W} = tabular_CPD(bnet2, W, 'prior_type', 'dirichlet', 'dirichlet_weight', 0); % tabular_CPD生成多項式條件概率

#顯示估計的引數#

Parameter_MLE=bnet2;
CPT_MLE=cell(1,N);
for i=1:N
    s=struct(Parameter_MLE.CPD{i});
    CPT_MLE{i}=s.CPT;
end

Parameter_MLE_W = CPT_MLE{4};

#從完全觀察到的資料中查詢MLE#
#先驗0的貝葉斯更新等效於ML估計#

% Find MLEs from fully observed data 從完全觀察到的資料中查詢MLE
bnet4 = learn_params(bnet2, samples); %LEARN_PARAMS查詢完全觀察的模型的最大似然引數

% Bayesian updating with 0 prior is equivalent to ML estimation 先驗0的貝葉斯更新等效於ML估計
bnet5 = bayes_update_params(bnet2, samples);  %給定完全觀察到的資料，BAYES_UPDATE_PARAMS貝葉斯引數更新

#顯示學習引數結果#

% MLE
CPT4 = cell(1,N);
for i=1:N
  s=struct(bnet4.CPD{i});  % violate object privacy
  CPT4{i}=s.CPT ;
end
CPT4{4}

% Bayesian
CPT5 = cell(1,N);
for i=1:N
  s=struct(bnet5.CPD{i});  % violate object privacy
  CPT5{i}=s.CPT ;
  assert(approxeq(CPT5{i}, CPT4{i}));
end
CPT5{4}

三、耗時統計

T=cputime;
…
E=cputime-T;
disp(E)

---

結果

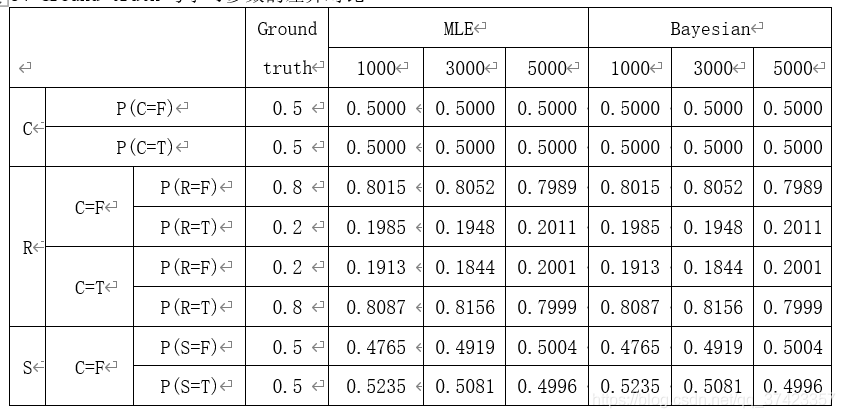
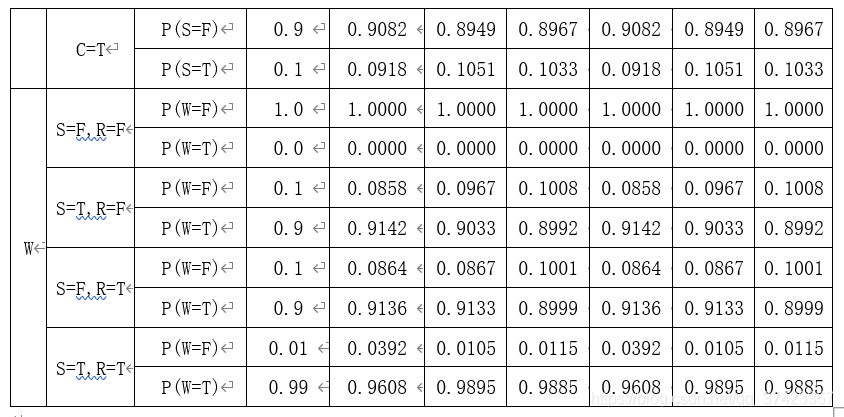
由上表資料可以觀察到，MLE與Bayesian學習到的條件概率基本一致；並且隨著學習資料量的增加，學習到的條件概率表越來越逼近於Ground truth的條件概率表。