北郵 python 問題 C: 排隊前進

題目描述

有 n 個人排隊向一個方向前進，他們前進的速度並不一定相同。 最開始即 t=0 時，每個人的位置並不相同。可以把他們放在數軸上，設他們前進的方向為正方向,對於從左往右第 i 個人,編號為 i，他的初始位置為xi ,初始速度為vi。編號為1的人（隊尾，位於數軸最左側）的位置總為座標原點,即總有x1=0。(位置單位為米,速度單位為米每秒)。 雖然他們的前進速度不同，但是他們要保證前後順序不能變。即i追趕上 i+1 的時候, i 將會緊跟 i+1 以 i+1 的當前速度前進.可以認為他們是緊挨著的,之間的距離可以忽略不計。 求編號為1的人前進 s 米需要多少秒.
輸入
第一行兩個整數n,s,其中(1<=n,s<=100,000),代表n個人排隊前進,以及最後的一個人需要前進的距離為s米。 接下來n行,每行兩個整數xi,vi,代表第i個人的位置xi,以及他的初始速度vi,保證(0=x1≤x2≤…≤xn≤100,000,1≤vi≤100,000)。
輸出
輸出一個小數,按照四捨五入的原則恰好保留小數點後兩位（測試資料保證答案的小數點後第三位不是4或5）。

樣例輸入 Copy

3 4
0 3
1 2
2 1

樣例輸出 Copy

2.00

---

思路

第一種方法：按照最常見的思路方式，

• 第一步，查詢相鄰兩個隊員之間相遇的最短時間，即全部遍歷一遍
• 第二步，在找到最短時間之後，進行每一位隊員的座標的更新
• 第三步，根據被更新後的座標，更新速度，即可。
• 第四步，迴圈以上三個步驟即可（需要注意的是，在更新距離的時候，需要判斷x1是否到達s,進行相應的處理）

第二種方法：

• 第一步，從佇列的最後往前遍歷，直到某一位隊員的位置恰好小於等於s
• 第二步，計算與s座標最近的隊員X(m)的耗時 tq，再次計算X(m-1)的耗時 th（需要注意的是，前面的隊員的速度不能夠超過後面的隊員的速度）
• 然後th = max{ th , tq}
• 重複2，3步驟，遍歷完一遍即可。

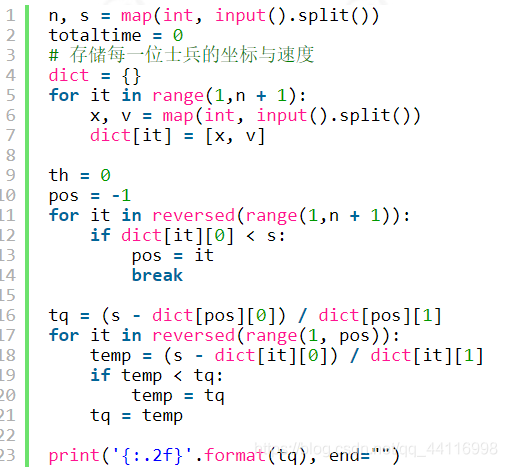
程式碼解析