身份隱私保護技術

混淆服務

• 混淆服務的目的在於混淆訊息雙方的聯絡（如 圖 2 所示）。當傳送方需要告知接收方訊息 M 時， 它會首先用接收方的公鑰 KB 加密 M，並在密文後 附帶真實接收地址 R。為了藉助第三方（圖 2 中的 混淆伺服器）的能力隱藏交易雙方的關聯性，傳送 方會繼續用第三方的公鑰 KI 做第二重加密，並將結果（見下方公式的箭頭左側）提交給第三方。

• 當第三方接收到若干密文後，分別進行解密以獲取原始密文，並根據解密出來的地址進行轉發 ； 接收方收到訊息後可自行解密獲知訊息 M。整個過程用加密方式保證接收方地址不可見，用雙重亂數保證每次對談之間不可連結。當第三方處理的交易達到一定數量時，可以有效實現訊息來源與目的地之間關係的混淆。
• 這種方式部署簡單，且與區塊鏈有很好的相容性，因此得到廣泛採用。現有的研究進展主要集中在中心化混淆和分散式混淆兩個方面。

中心化混淆

• 中心化混淆是指混淆服務由單一實體提供，例 如單個伺服器、企業等。
• 目前有多家網站提供有償 混淆服務，例如 Onionbc、Bitcoin Fog、Bitmixer 等。 他們可以有效隱藏交易地址，但是存在一定的缺陷： (1) 服務提供商本身是潛在的攻擊者，存在支付抵賴等欺詐風險 ；(2) 處於中間位置的混淆服務提供商有機會知道並記錄交易雙方的資訊。

第一個問題的解決措施

• 針對第一個問題，即交易的公平性。
• 條件執行是可行的方式之一。它設定當且僅當混淆服務商誠實執行混淆服務後，才可以獲得服務費，否則什麼都得不到。格雷戈裡·麥克斯韋 (Gregory Maxwell) 為位元幣設計了 CoinSwap 協定 ，允許交易發起者設定雜湊鎖關聯到特定的贖回指令碼，防止數位資產被竊取。
• 另一種解決方法是可信審計，即混淆伺服器留下可信憑證，若出現違規行為則可以進行有效追責。例如 Mixcoin基於簽名機制保證審計過程的不可抵賴性。
• 2015 年釋出的達世幣 (Dash) 嘗 試從經濟學角度解決中心化混淆方案面臨的隱私洩 露問題。該方案中，混淆節點負責彙集並生成混淆 方案，通過預付保證金的方式提高違規代價。
• 然而， 這幾種方案中混淆伺服器仍掌握著交易地址間的關聯資訊。

第二個問題的解決措施

• 盲簽名是解決第二個問題的有效方法之一，一 般包括 3 個階段 ：盲化（使用隨機盲化因子隱藏訊息），簽名（簽名者對盲化後的訊息做簽名），去盲化（去掉盲化因子，提取出對訊息的有效簽名）。此類簽名的特點是待簽名的訊息對簽名者不可見。因 此，Blindcoin[4] 將盲簽名的思想引入 Mixcoin 中， 既可提供對不當行為的審計憑證，又可以保證混淆 伺服器無法分辨所籤交易接收方的地址是哪個，從而保證地址資訊的隱私性。然而，這種機制要求交易金額必須是固定的，且這種方案無法避免混幣節 點的違規行為。
• TumbleBit[5] 首次同時實現了交易不可連結性 和防資產盜竊。它的思路是利用安全兩方計算來 保證使用者隱私和交易公平性，主要包括 3 個步驟 ： (1) Puzzle-Promise 階段，接收方與混淆伺服器建立 託管交易，加密贖回指令碼，並將密文盲化後轉交給 傳送方。(2) 傳送方與混淆伺服器執行安全兩方計算完成解密。在該過程中，傳送方會採用條件交易的方式保證雙方的公平性。(3) 接收方將答案去盲化， 贖回託管交易。

問題

• 上述中心化的混淆方案具有易操作性，但是普遍存在 3 個弊端 ：(1) 時延較長，需等待足夠多的混 淆請求者，以保證混淆效果 ；(2) 集中式的混淆伺服器易遭受拒絕服務 (DoS) 攻擊 ；(3) 實際應用中需要支付額外的混淆費用。

分散式混淆

• 為了減輕因集中式構架帶來的單點威脅，同時節約混淆成本，研究人員開始思考分散式的交易混淆模式，即由多個互相不完全信任的對等實體共同執行匿名交易釋出，而無需第三方代理。
• 目前主流 的解決方法有 CoinJoin[6] 和安全多方計算 (MPC)。
• CoinJoin[6] 的核心思想是「尋找志同道合者一 起交易」。圖 3 可以直觀地解釋 CoinJoin 的思路。

• 現有由兩筆交易 A → C 和 B → D 待支付（圖 3 左 側），CoinJoin 將這兩筆交易揉在一起形成一筆 2 輸 入、4 輸出的交易，外部觀察者是無法分辨出這兩筆交易的。CoinJoin 因其與位元幣的高度相容性（僅 需利用修改位元幣協定的多重簽名機制），提出之後很快被應用於工程上，例如 Dark Wallet、Joinmarket 等。 但是 CoinJoin 機制還留有 3 個值得改進的地方 ： 1. 缺乏內部不可連結性。以圖 3 為例，參與者 A 和 C 是明確知道對方交易資訊的。隨著參與者數量增多，遭受 Sybil 攻擊的可能性也會提高（即某參與者是惡意攻擊者假扮的）。 2. 易受 DoS 攻擊。此類 DoS 攻擊是指攻擊者 通過拒絕簽署贖回指令碼，導致整個交易無法贖回， 由於位元幣交易不可復原，這種攻擊很可能會造成嚴重的資產損失。 3. 從實用的角度來講，CoinJoin 受制於參與者人數，若人數過少，則無法達到匿名性要求 ；若人數過多，則通訊開銷呈指數級增長，且提高了被 DoS 攻擊的風險。 隨後的方案針對這三個問題進行了改進 ：Coin- Shuffle[7] 採用層層加密和隨機置換的方式洗牌輸出 地址，即便是參與者也不知道交易地址間的關聯性。 但是，這種方案以高通訊和計算成本為代價，同時 對因攻擊者拒絕簽署贖回指令碼而造成損失的狀況仍 束手無策。
• 安全多方計算指的是參與者在無須歸集私有資料的情況下完成協同計算，同時保護各資料所有方的原始資料隱私。CoinParty[8] 就是基於安全多方計 算優化分散式混淆過程的一種改進協定，設定交易 的贖回指令碼須參與方執行門限簽名， 容忍一定數量節點的失效或惡意操作， 可以有效對抗 Sybil 或 DoS 攻擊。

環簽名

• 分散式混淆機制需要等待其他參與者一起執行混淆協定，這個過程取決於何時找到具有共同交易意願的人， 因此等待時延難以預計。而環簽名機制，允許使用者在無需其他「環」成員 線上的情況下，自行簽名，且關於公鑰的資訊隱藏於整個「環」中，有效保障了簽名的身份隱私需求。

原理解釋

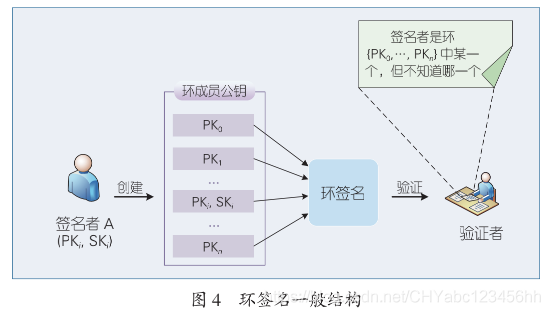
• 一般環簽名的思路如下圖所示，假定「環」中有n 個成員（各自擁有一對公私鑰），簽名者 A 使 用公鑰集合{pk1, …, pkn}和自己的私鑰ski產生簽名。 這個簽名的某個引數根據一定規則呈環狀，環簽名 由此得名。驗證者只能夠驗證簽名結果的合法性， 但無法確定真正的簽名者。通過此方法，簽名者可 以自由指定自己的匿名範圍，並且無須等待環成員線上，可以提供非常優美的匿名性保護。
• 可連結環簽名是環簽名的一個變種，設計初期是為了滿足同一個簽名者籤相同訊息時的追責需求，例如匿名投票。在環簽名的基礎結構之上，每 個簽名還附帶有標籤 T=(issue, PK)，其中 PK 表示圖 4 的環成員公鑰集合，issue 是選票的標籤。

• 驗證者使用 T=(issue, PK) 而非 PK 來驗證環簽名，此時可以保證 ： 1. 由不同的標籤 T 產生的任何簽名都是不可連結的 ；2. 用相同的 T 籤兩個不同的訊息，可以及時被發現（即可連結性），但仍可隱藏真實身份。

CryptoNote 和 Monero

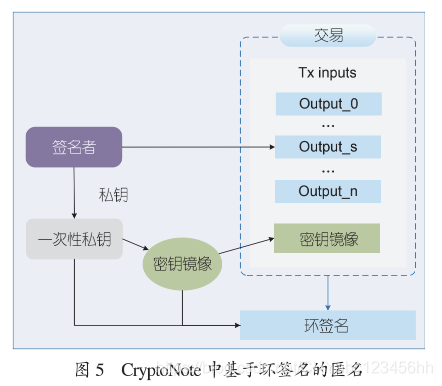
• 區塊鏈有防雙重支付的需求，因此若想使用環簽名保護簽名者的身份隱私，就需要採用可連結環簽名的思路（見圖 5）。在 CryptoNote[9] 中，簽名者 使用一次性私鑰生成金鑰映象，作為 T 中的 issue附在交易贖回指令碼中。若同一交易贖回兩次，則可 以被及時發現並判定無效。

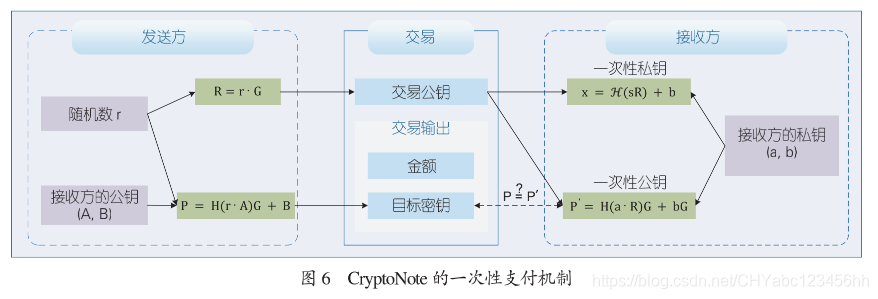
• 除了使用可連結環簽名保證傳送方的身份隱私外，CryptoNote 在接收端設定每筆交易僅使用一次 性公私鑰對（如圖 6 所示的一次性支付 (one-time payment) 機制），即交易的輸出目的地址是一個僅可以由傳送方和接收方生成的公鑰地址，該地址中 包含有亂數，交易贖回後即丟棄，保證交易目標地址不會重複。 但 CryptoNote 明文形式的交易金額會削弱匿名性效果。因此，2014 年公佈的 Monero 幣借鑑 CryptoNote 的思想，結合可連結自發匿名環簽名 (MLSAG) 和機密交易 (Confidential Transaction, CT)， 設計環上的機密交易 RingCT[10]，把交易金額隱藏在同態密文之後，同時實現了身份隱私和交易隱私。

非互動式零知識證明

• 非互動式零知識證明 (Non-Interactive Zero- Knowledge proof, NIZK) 是零知識證明的一種，支援 證明者在不提供任何有用資訊的情況下，向驗證者 證明某論斷。這個過程不需要雙方同時線上互動， 因此非常適合應用於區塊鏈中進行匿名的訊息驗證。

原理解釋

• 一般的 NIZK 形式化定義為 ：假定概率多項 式時間演演算法 (P, V) 分別代表證明者和驗證者，那麼 對於任意安全引數為 k 的描述 ℒ⊆NP，若 (P, V) 是 NIZK 系統，則需滿足以下 3 個性質 ：

正確性

• 對於任意 x∈ℒ 及其特定證據 w， 滿足如下的公式所示，即若 P 知道論斷 x 的證據 w，則一定能通過有 效演演算法使 V 相信它。

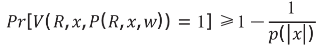
完備性

• 對於任意 x∉ℒ 和概率多項式演演算法 P*，滿足如下的公式，即若 x 是錯誤論斷，則一定不存在有效演演算法使 V 相信它

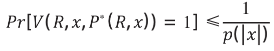
零知識性

• 對於任意 x ∈ ℒ 和特定證明 w， 存在概率多項式時間模擬器 S 使得以下兩組分佈計 算不可區分 ：

• 即驗證者看到的資訊也可以通過一個概率多項 式時間模擬器來模擬，驗證者沒有獲得任何額外信 息。描述中 p(·) 代表多項式，R 代表 NIZK 系統中 的公共參考串 (Common Reference String, CRS)。

Zerocoin 和 Zerocash

• Zerocoin首次將 NIZK 應用於區塊鏈，讓區塊鏈節點在不知道具體交易內容的情況下驗證交易的有效性，既保留區塊鏈互相不信任的個體間的共 識達成問題，又可以保護使用者隱私。其主要思想類 似於分散式混淆機制，交易前首先熔鑄一個數位貨 幣，然後用一個等價的全新數位貨幣兌換，其中熔 鑄數位貨幣的真實性和有效性由 NIZK 系統來驗證。 具體過程可以形式化為「熔鑄→公佈→兌換」 三個步驟。
• 例如 ：A 打算向 B 支付一個數位貨幣。 首先，A 計算隨機序列號 sn，用陷門 r 對它做承諾， 得到 cm（該承諾值僅可以通過 (sn, r) 來開啟，但無 法計算出 (sn, r)）。然後，A 釋出帶有 cm 的熔鑄交易， 區塊鏈節點對執行共識演演算法進行驗證和記錄。B 在 做數位貨幣兌換時需要提供關於如下論斷的零知識 證明 π ：1, 公共賬本中有某個特定的承諾 cm ； 2, B 知道該承諾對應的陷門 r，開啟為 sn。 如果 cm 的驗證是正確的，並且 sn 未被使用過， 則 B 可以贖回一個新的數位貨幣 ；否則本次兌換將 因為驗證失敗而被拒絕。在這個場景中，A 熔鑄的 數位貨幣與 B 贖回的數位貨幣並無任何關聯，這是因為零知識證明 π 保證不會洩露關於 cm 或 sn 的任 何有效資訊。

問題

• 但是 Zerocoin 並不完善，依舊存在一些值得改 進的地方 ： 1. 在上述範例中，A 也知道 sn 和陷門 r，有可 能在 B 兌換之前先執行兌換過程，或者當 B 繼續做 數位貨幣交易時，通過追蹤 sn 來發現 B 的交易資訊。 2. 匿名交易的面額固定，缺乏應用的靈活性。 3. 交易直接公佈在公共賬本中，未對交易資料 隱私做特殊保護。 Zerocash 針對上述問題進行了改進，配合 zk- SNARK (zero-knowledge Succinct Non-Interactive Arguments of Knowledge) 和加密方案同時保護身份 和交易隱私。

交易隱私保護技術

• 當前區塊鏈中實現交易隱私保護的兩項密碼技 術有 ：非互動式零知識證明和同態技術。

非互動零知識證明

• Zerocash[12] 首次應用 zk-SNARK 提供完全的用 戶隱私化和交易資訊隱藏化。
• 與 Zerocoin 相比，它 的優勢體現在以下 3 個方面。
• 1. zk-SNARK 具有簡潔性，即驗證者只需要少 量計算就可以完成驗證 ；非互動性，即整個證明過 程僅需交換少量資訊。這兩個性質對於區塊鏈非常 友好，因為區塊鏈上節點眾多，為了能夠快速達到 共識，計算複雜度和通訊成本都不能過大。
• 2. 修改數位貨幣承諾的生成方案，並使用偽隨 機函數來確定支付目標地址和序列號，即當數位貨 幣兌換後，接收方會用私鑰產生全新的序列號 sn’， 確保即使傳送者知道之前的 sn，仍然無法跟蹤或兌 換該數位貨幣。
• 3. 支援任意金額的區塊鏈交易，且通過加密技 術保證交易金額、交易亂數、交易目標地址等信 息的隱蔽性。同時，為了驗證交易，會在零知識證 明中增加關於交易金額有效性的驗證。

問題

• 以太坊 (Ethereum) 目前也在試圖把 Zerocash 的 隱私交易功能作為一個預編譯合約連結到智慧合約中，即 ZoE (Zcash over Ethereum) 工程，不過即使做了預編譯優化，它能提供的隱私驗證能力也非常 有限。Hawk 則是一個完全採取 zk-SNARK 的區 塊鏈智慧合約部署系統，保證了資料和計算過程在 鏈上的隱私性和可用性，在保險、股票等金融領域 有著廣泛的應用前景。

同態加密技術

• 同態密碼是一類保持密文延展性的加密方案， 支援將密文操作對映到原始資料上，具有天然的數 據隱私性保護。以場景為例，參與方 A 擁有資料 {x1, …, xn}，參與方 B 擁有計算邏輯 f(·)，二者想共 同計算 f(x1, …, xn)。定義 E(·)/D(·) 為一組同態加密 方案的加 / 解密演演算法。首先，A 分別對資料進行加密， 將加密結果 {E(x1), …, E(xn)} 傳送給 B。此時 B 按照 f 的計算邏輯執行運算得到 = f(E(x1),…,E(xn))，將 返回給 A。這時，A 使用解密演演算法對結果進行解密， 就可以獲得計算結果 f(x1, …, xn)。 在這個過程中，B 僅擁有密文且無法獲知 A 的資料，有效保證了資料的隱私性。區塊鏈隱私保護中常用 的同態密碼技術有 Pedersen 承諾和 Paillier 加密。

Pedersen 承諾

• Monero 基於機密交易機制保 證交易資料的隱私性，該機制使用 到的核心技術之一就是 Pedersen 承 諾。在機密交易中，交易金額提交 到區塊鏈前首先由隨機盲化因子進 行承諾。在交易驗證過程中，由 於 Pederson 承諾的同態性，可以分 別計算交易的輸入和輸出密文的總 和，通過驗證「所有輸入輸出的總 和是否為關於 0 的承諾」來驗證交 易金額的有效性。此時交易發起者 僅需要證明他知道承諾對應的亂數，這個證明可以使用一個標準的零知識證明來實 現，整個過程不會洩露交易的實際金額或其他交易 資料。

Paillier 加密

• Paillier 是基於複合剩餘類基本假設的同態加 密方案，它的加 / 解密形式簡單，且密文無噪聲。 Wang 等學者 [14] 使用 Paillier 加密方案構造了針對比 特幣的隱私交易系統，其中交易金額使用 Paillier 進 行隱蔽性保護，零知識證明用於檢查加密後金額的 有效性（即確保交易金額為正，並驗證輸入之和等 於輸出之和）。這些交易就像密封的資產信封，可 以合併、分離或使用，並且保持金額不可見。 另一個基於 Paillier 構造的區塊鏈隱私計算工程 是由矩陣元公司推出的計算平臺 PlatON。該平臺重 點針對以太坊的餘額模型進行資料隱私保護，設計 並部署基於 Paillier 的使用者賬戶餘額的密態更新，並 提出一種新的非互動式零知識證明方案 [15]，用於驗 證密態交易資料的合法性。然而，這種方案解密的 時候需要求解橢圓曲線離散對數問題，在交易金額較大的時候解密性比較差。

總結與展望

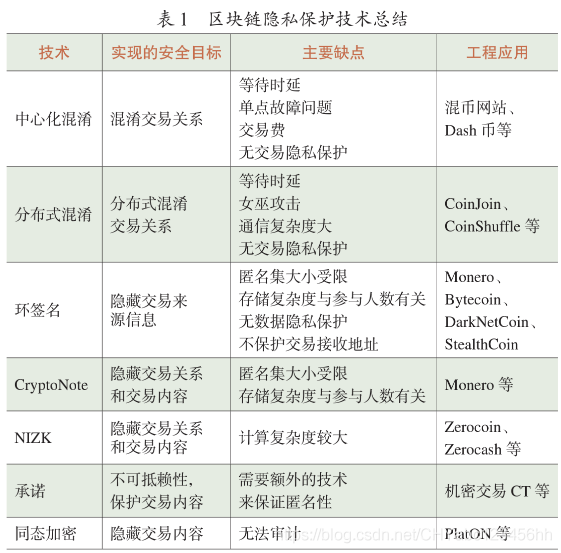
• 1. 可延伸性和經濟性 如表 1 所示，中心化 和分散式混淆方法都會產生額外的等待延遲，Zero- cash 的證明平均生成時間約為 2 分鐘，CryptoNote 中匿名交易簽名的大小與參與者的數量成正比，這 意味著儲存和通訊成本也會隨匿名集的增大而增 加。因此，如何優化組合現有的隱私保護方案或設 計低成本的密碼方案是一個值得研究的方向。
• 2. 弱假設下的強隱私保護 分散式混淆假 設一定比例的參與者是誠實的，以緩解 Sybil 攻擊 的危害 ；zk-SNARK 需要第三方生成初始化電路 ； Hawk 中每個智慧合約都需要一個獨立的可信的初 始化程序。從優化安全性模型的角度來看，新的隱 私保護方案需要儘量少的安全性假設，從而增強實 際隱私保護效果。
• 3. 相容性 區塊鏈有兩種主流的交易模式 ： 位元幣為代表的 UTXO 和以太坊為代表的 AC- COUNT。現有方案大多針對 UTXO 模型（鏈式結構） 進行隱私保護。在 ACCOUNT 模型中，賬戶為全球 狀態，交易決定賬戶狀態，相互之間沒有聯絡。此 時混淆交易地址無法達到隱私效果，因此隱私保護 方法與 ACCOUNT 架構相容是一項新的待解決問題。
• 4. 合法監管性 區塊鏈的隱私保護是一把「雙 刃劍」。一方面，誠實使用者希望擁有資訊的隱私性 ； 另一方面，惡意實體可能濫用隱私保護機制進行某 些非法交易。因此，區塊鏈隱私需要具備條件性， 即權威機構可以被授權跟蹤目標使用者的區塊鏈行 為，並收集他 / 她已經傳播的所有訊息，但該使用者 的敏感資訊仍然受到保護。
• 區塊鏈概念自提出至今一直受到學術界和產業界的廣泛關注。它提供了一種完全分散式的、不可 篡改的資料儲存、共用和同步方式，非常適用於大 型分散式網際網路互動系統（例如物聯網或供應鏈系 統）。近幾年，全行業都在尋求如何使用區塊鏈來 解決各領域存在的痛點。 但是，在網際網路時代，資料即資產。日益增長 的隱私保護需求是區塊鏈落地實用前必須面對並解 決的問題之一。希望本文能為區塊鏈相關隱私問題 的探索提供引導與啟發。