語音訊號處理基礎知識

1.均值

1.1.均值公式定義

$$\overline{x}=\frac{x_1+x_2+\cdots +x_n}{n}=\frac{{\sum }_{j=1}^n{x}_j}{n}$$

1.2.物理意義

一段語音訊號的均值代表了語音的直流分量, 正常情況下音訊系統的輸入輸出不存在交流分量。 如果發生了直流偏執的現象, 需要在訊號預處理階段去除直流分量。

1.3.程式碼實現

讀取一段新聞語音檔案, 計算它的均值。

from scipy.io import wavfile
import numpy as np

framerate, data = wavfile.read('./source.wav')
data_len = len(data)
sum = 0
for i in range(data_len):
    sum += data[i]
mean_data = sum / data_len
print('mean of audio : %f' % mean_data)

mean of audio : -0.000320

numpy提供average函數來計算均值, 效果一致。

np.average(data)

-0.000320226621917049

可以看出， 均值接近0.

2.方差

2.1.方差的公式定義

$$s^2=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}{)}^2$$

2.2.物理意義

方差描述語音訊號的波動範圍, 交流分量的強弱, 即交流訊號的平均功率。

2.3.程式碼實現

sum = 0
for i in range(data_len):
    sum += (data[i] - mean_data) ** 2
var_data = sum / data_len
print('var of audio : %f' % var_data)

var of audio : 3197990.844967

numpy提供var函數用以計算方差, 效果一致。

np.var(data)

3197990.8449671054

3.均方差

3.1.均方差的公式定義

$$\sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}{)}^2}$$

3.2.物理意義

均方差等於方差的方根, 和方差一樣可以反映語音訊號的離散程度。由於方差的平方計算造成量綱的倍數變化無法直觀反映出偏離程度, 均方差的意義更為直觀。

3.3.程式碼實現

sum = 0
for i in range(data_len):
    sum += (data[i] - mean_data) ** 2
rmse_data = np.sqrt(sum / data_len)
print('rmse of data : %f' % rmse_data)

rmse of data : 1788.292718

numpy提供std函數用以計算均方差, 效果一致。

np.std(data)

1788.2927179203928

4.協方差

4.1.公式定義

$$Cov(X,Y)=\frac{{\sum }_{i=0}^n(X-\overline{X})(Y-\overline{Y})}{n-1}$$

4.2.物理意義

描述兩個變數之間的變化趨勢相關性

4.3.程式碼模擬理解

計算初始相位0， π之間

def cov(x, y):
    avr_x = np.average(x)
    avr_y = np.average(y)
    sum = 0
    for i in range(len(x)):
        sum += (x[i] - avr_x) * (y[i] - avr_y)
    return sum / (len(x) - 1)

import matplotlib.pyplot as plt

x = np.arange(0, 10 * np.pi, 0.1)
y_1 = np.sin(x)
plt.plot(x, y_1)
plt.xlabel('sample (n)')
plt.ylabel('amp')
plt.show()

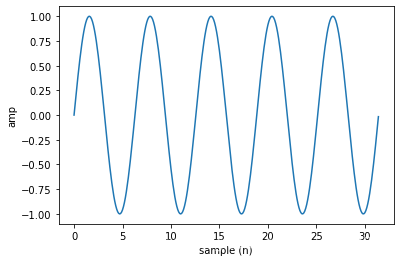
初始相位為0的正弦訊號影象

y_2 = np.sin(x + np.pi)
plt.plot(x, y_2)

[<matplotlib.lines.Line2D at 0x7efef0fbd2b0>]

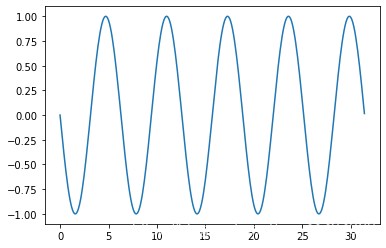
初始相位為0的正弦訊號影象,可以看出相位相差π的兩個序列的變化趨勢完全相反。計算這兩個訊號序列的協方差

print(cov(y_1, y_2))

-0.5002531220184325

numpy提供cov函數來計算協方差矩陣, 矩陣的次對角線是兩個序列的協方差。

np.cov(y_1, y_2)

array([[ 0.50025312, -0.50025312],
       [-0.50025312,  0.50025312]])

計算不同初始相位下, 兩個正弦序列的協方差變化情況。

phi_list = np.linspace(0, 2 * np.pi, 100)
cov_list = [cov(np.sin(x), np.sin(x + phi)) for phi in phi_list]
plt.plot(phi_list, cov_list)

[<matplotlib.lines.Line2D at 0x7efef0af0208>]

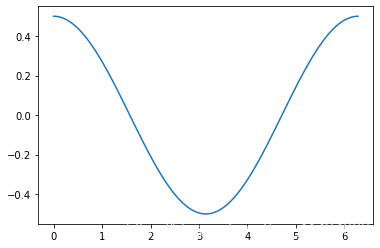
5.分幀加窗以及頻譜洩露

5.1.頻譜洩露

計算離散傅立葉變換的前提是假設輸入有限長度的訊號序列是一個週期訊號的一個完整週期, 週期長度為該序列的長度。離散傅立葉變換本質是以該序列長度為週期進行週期延拓後的週期訊號, 計算這個無限週期序列的頻譜圖。由於dft計算出的頻譜對應的是週期延拓後的週期訊號, 如果有限長的訊號的首尾不相等, 會使得週期延拓後的週期訊號不連貫, 會帶來一些本來不屬於訊號本身的頻率分量。

下面定義dft實現如下:

import math

def dft(x):
    """
    :bref 計算輸入序列的離散傅立葉變換

    :param x : 輸入序列
    :param N : dft長度N
    :return spectrum : 頻譜
    """
    N = len(x)
    spec = np.zeros(N)
    for k in range(N):
        sum = 0
        for n in range(N):
            sum += x[n] * np.exp(-1j * 2 * np.pi * n * k / N)
        spec[k] = abs(sum / N)
    return spec

定義計算頻譜對應的頻率值函數:

def dft_freq(N, sample_rate):
    """
    :bref 計算對應的頻域解析度

    :param N : DFT點數
    :param sample_rate : 取樣率
    :return freqs : 對應的頻域的取樣率
    """
    freqs = sample_rate / N * np.array(range(N))
    return freqs

採用頻率為10的正弦訊號, 使用五個整數倍週期作為訊號的長度; 從繪製的波形圖可以看出整數倍週期的首尾是連貫的。

def create_sin(Ts, freq, times):
    sample_rate = 1 / Ts
    freq = 10
    T = 1 / freq
    duration = times * T
    samples = math.ceil(duration / Ts)
    t = Ts * np.array(range(samples))
    x = np.cos(2 * np.pi * freq * t)
    return t, x

Ts = 0.01
t, x = create_sin(Ts, 10, 5)
plt.plot(t, x)

[<matplotlib.lines.Line2D at 0x7efeef8ec5c0>]

將該訊號進行週期延拓三次, 可以看出週期延拓後的訊號和原本一致。

def sig_append(x, times, Ts):
    """
    :bref 週期延拓

    :param x : 需要週期延拓的訊號
    :param times : 延拓次數
    :param Ts : 取樣週期
    :return t_add : 延拓後序列的時間
    :return x_add : 延拓後的訊號幅值
    """
    N = x.shape[0]
    t_add = Ts * np.array(range(N * times))
    x_add = np.zeros(N * times)
    for i in range(times):
        x_add[i * N:(i + 1) * N] = x[:]
    return t_add, x_add

t_add, x_add = sig_append(x, 3, Ts)
plt.plot(t_add, x_add)

[<matplotlib.lines.Line2D at 0x7efeef56d860>]

使用dft計算該訊號頻譜, 可以看出頻譜分量只有10Hz。

freq_dft = dft_freq(x.shape[0], 1 / Ts)
plt.plot(freq_dft, dft(x))
plt.xlabel('Freq (Hz)')
plt.xlim([0, freq_dft[-1] / 2])
plt.show()

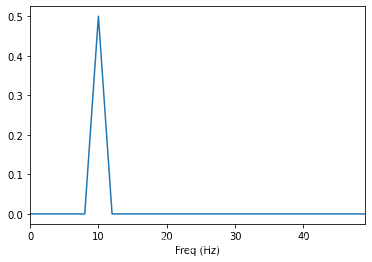
將訊號長度改為非整數倍週期5.2, 來看看時域頻域的效果。

t_5_2, x_5_2 = create_sin(0.01, 10, 5.2)
plt.plot(t_5_2, x_5_2)

[<matplotlib.lines.Line2D at 0x7efeec7f6908>]

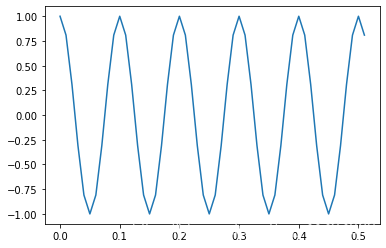
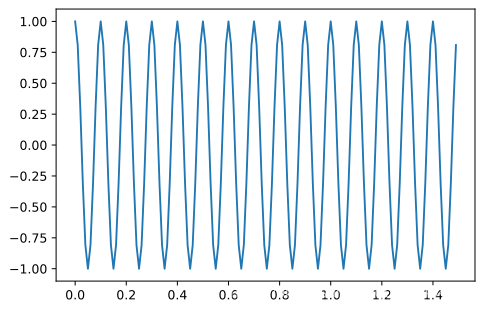
同樣的, 將週期進行三倍延拓看看效果。可以發現在延拓交界點存在不期望的波形。

t_add, x_add = sig_append(x_5_2, 3, Ts)
plt.plot(t_add, x_add)

[<matplotlib.lines.Line2D at 0x7efeed7d9cf8>]

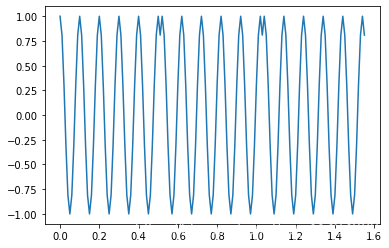
來看看頻域的效果, 可以發現在10Hz分量之外還有其他的頻率分量, 整個訊號的能量從基頻洩露了一部分到其他頻率上, 這就是頻譜洩露。

freq_dft = dft_freq(x_10_1.shape[0], 1 / Ts)
plt.plot(freq_dft, dft(x_10_1))
plt.xlabel('Freq (Hz)')
plt.xlim([0, freq_dft[-1] / 2])
plt.show()

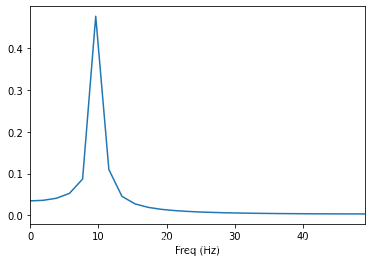
可以通過對訊號的首尾進行抑制來減弱首尾不連貫帶來的頻譜洩露, 即就是加窗。
漢寧窗的數學定義是:

$w(n)=0.5\times (1-cos(2\pi n/(N-1))),0\le n\le N-1$

定義生成漢寧窗的函數如下:

def create_hanning(N):
    window = np.arange(N)
    window = (1 - np.cos(window / (N - 1) * 2 * np.pi) + 1) / 2
    return window

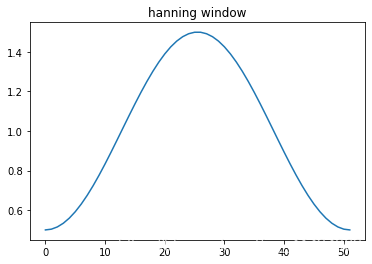
對5.2倍週期的訊號進行漢寧窗加權, 可以看到首尾的訊號被衰減了。

window = create_hanning(x_5_2.shape[0])
x_5_2_window = x_5_2 * window
plt.figure(0)
plt.title('hanning window')
plt.plot(range(window.shape[0]), window)
plt.figure(1)
plt.title('after window')
plt.plot(t_5_2, x_5_2_window)

[<matplotlib.lines.Line2D at 0x7efeec381358>]

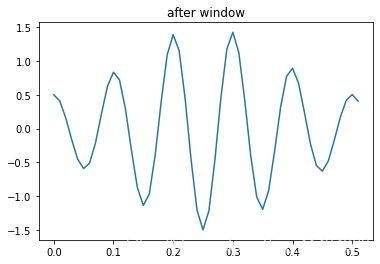
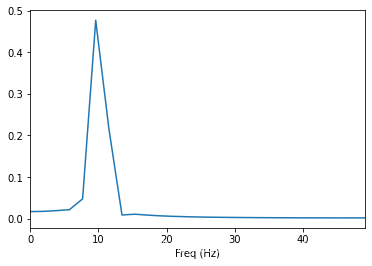
繪製對應的頻譜圖, 可以看出非10Hz的訊號分量少了很多。

freq_dft = dft_freq(x_5_2_window.shape[0], 1 / Ts)
plt.plot(freq_dft, dft(x_5_2_window))
plt.xlabel('Freq (Hz)')
plt.xlim([0, freq_dft[-1] / 2])
plt.show()

def frame_sig(sig,frame_len,frame_step,winfunc=lambda x:numpy.ones((x,))):
    """
    :bref 將訊號進行分幀加窗處理

    :param sig: 需要分幀加窗的語音訊號.
    :param frame_len: 幀長.
    :param frame_step: 幀移.
    :param winfunc: 窗函數, 預設為矩形窗.
    :returns: 分幀後的資料.
    """
    slen = len(sig)
    frame_len = int(round_half_up(frame_len))
    frame_step = int(round_half_up(frame_step))
    if slen <= frame_len:
        numframes = 1
    else:
        numframes = 1 + int(math.ceil((1.0*slen - frame_len)/frame_step))

    padlen = int((numframes-1)*frame_step + frame_len)

    zeros = numpy.zeros((padlen - slen,))
    padsignal = numpy.concatenate((sig,zeros))

    indices = numpy.tile(numpy.arange(0,frame_len),(numframes,1)) + numpy.tile(numpy.arange(0,numframes*frame_step,frame_step),(frame_len,1)).T
    indices = numpy.array(indices,dtype=numpy.int32)
    frames = padsignal[indices]
    win = numpy.tile(winfunc(frame_len),(numframes,1))
    return frames*win

np.fft.fft

<function numpy.fft.fft(a, n=None, axis=-1, norm=None)>