2020電賽E題--非線性失真器程式設計--01--演演算法模擬與STM32FFT資料驗證(附工程原始碼+gitee連結)
寫在前面
20電賽整體感覺難度比之前小,本次程式設計上也沒有太多的難點。功能指標全部完成,程式實現了測量每種失真的情況下的THD的近似值。並且進行了程式拓展,實現了全自動的測量,以及顯示測量波形的波形圖,頻譜圖。根據題目要求,我們可以看出這次程式設計要用到FFT演演算法。
我們的程式設計有兩個版本,一個版本是通過定時器進行取樣得到特定取樣率下的資料並儲存在陣列裡,然後進行傅立葉變換,另外一種就是通過定時器產生PWM波生成ADC的取樣時鐘,直接通過DMA儲存資料然後進行傅立葉變換。
在理論計算下,
所以本文主要介紹我們實現的FFT的功能測試驗證的程式。
題目
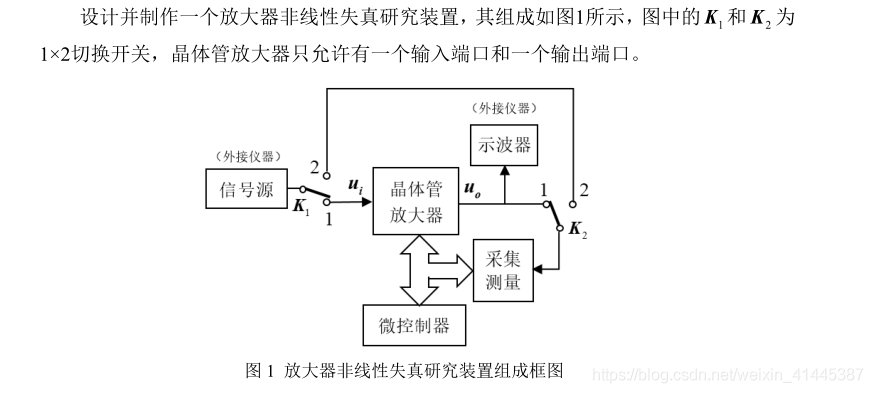
比賽指標要求

為什麼需要FFT?
任何連續測量的時域訊號都可以表示為不同頻率的正弦波訊號的無限疊加。以累加的方式來計算該訊號中不同訊號的頻率、振幅和相位。所以本次測量就必須要使用FFT演演算法。
原理部分就參照下別人的貼文大家自行檢視:
超詳細易懂FFT(快速傅立葉變換)及程式碼實現
知識科普:THD
總諧波失真表明功放工作時,由於電路不可避免的振盪或其他諧振產生的二次,三次諧波與實際輸入訊號疊加,在輸出端輸出的訊號就不單純是與輸入訊號完全相同的成分,而是包括了諧波成分的訊號,這些多餘出來的諧波成分與實際輸入訊號的對比,用百分比來表示就稱為總諧波失真。一般來說,總諧波失真在500赫茲附近最小,所以大部分功放表明總諧波失真是用500赫茲訊號做測試,但有些更嚴格的廠家也提供20-20000赫茲範圍內的總諧波失真資料。總諧波失真在1%以下,一般耳朵分辨不出來,超過10%就可以明顯聽出失真的成分。這個總諧波失真的數值越小,音色就更加純淨。一般產品的總諧波失真都小於1%@500Hz,但這個數值越小,表明產品的品質越高。
所以在進行測試前我們就要先有個概念
對於訊號源輸出的1k的正弦訊號,總諧波失真的近似值越小,表示程式更精準,基本在1.0%以內。
對於訊號源輸出的1k的方波訊號,總諧波失真的近似值大約是0.3887(前5次諧波計算的近似值)
失真度測試儀測量的結果:
正弦波

方波

這裡解釋下為啥方波測量出來的是44.26%,這裡先給出方波的傅立葉變換式子
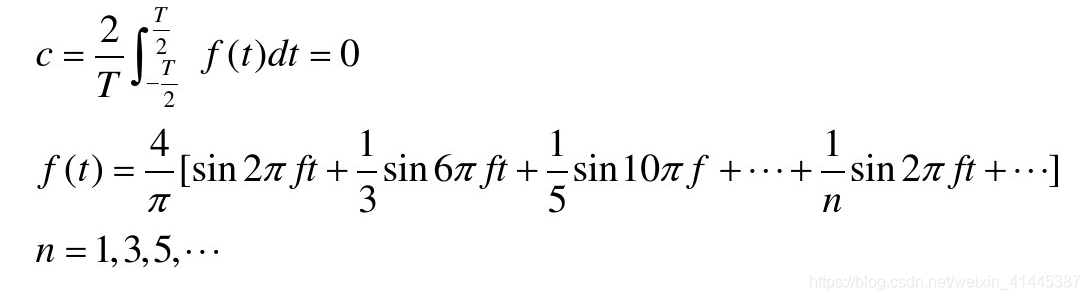
因為對於近似值來說方波取前五次傅立葉變換的值就是0.3887
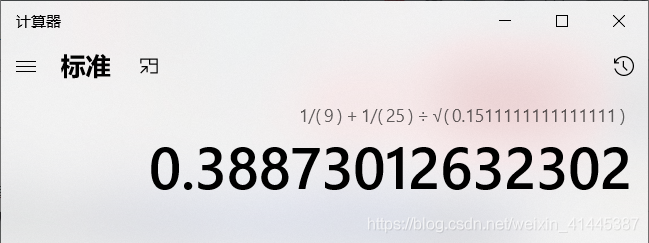
計算到前7次時候

MTLAB模擬測試
所以根據已有的知識,進行下MATLAB模擬測試
clf;fs=10240; %取樣頻率
Ndata=1024; %資料長度
N=1024; %FFT的資料長度
n=0:Ndata-1;
t=n/fs; %資料對應的時間序列
x=0.5*sin(2*pi*1000*t)+1; %時間域訊號
%subplot(2,2,4),plot(t,x);
subplot(2,2,2),plot(t,x,'.--');
y=fft(x,N); %訊號的Fourier變換
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真實頻率
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %繪出Nyquist頻率之前的振幅
xlabel('頻率/Hz');ylabel('振幅');
title('Ndata=10240 Nfft=1024');grid on;
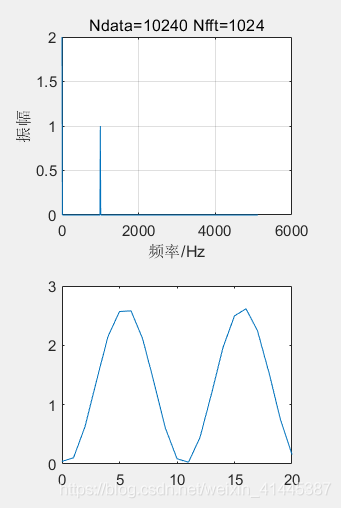
這裡模擬顯示的頻譜圖和我們的程式碼模擬給出的輸入訊號是相同的所以大致可以按照這個傅立葉變換的標準進行編寫程式碼。之所以這裡畫出取樣的波形圖是因為後面我們程式要畫波形圖,所以這裡就測試了下。理想波形的總諧波失真計算沒有意義所以就不進行計算。
STM32測試程式:
FFT.C
這裡的FFT也是找到的別人寫好的程式,所以就不做詳細講解了(能力有限)
#include "math.h"
#include "fft.h"
//精度0.0001弧度
//複數的交換
void conjugate_complex(int n,complex in[],complex out[])
{
int i = 0;
for(i=0;i<n;i++)
{
out[i].imag = -in[i].imag;
out[i].real = in[i].real;
}
}
//求所有複數的模
void c_abs(complex f[],float out[],int n)
{
int i = 0;
float t;
for(i=0;i<n;i++)
{
t = f[i].real * f[i].real + f[i].imag * f[i].imag;
out[i] = sqrt(t);
}
}
//求複數的和
void c_plus(complex a,complex b,complex *c)
{
c->real = a.real + b.real;
c->imag = a.imag + b.imag;
}
//求複數的差
void c_sub(complex a,complex b,complex *c)
{
c->real = a.real - b.real;
c->imag = a.imag - b.imag;
}
//求複數的積
void c_mul(complex a,complex b,complex *c)
{
c->real = a.real * b.real - a.imag * b.imag;
c->imag = a.real * b.imag + a.imag * b.real;
}
//求複數的商
void c_div(complex a,complex b,complex *c)
{
c->real = (a.real * b.real + a.imag * b.imag)/(b.real * b.real +b.imag * b.imag);
c->imag = (a.imag * b.real - a.real * b.imag)/(b.real * b.real +b.imag * b.imag);
}
#define SWAP(a,b) tempr=(a);(a)=(b);(b)=tempr
void Wn_i(int n,int i,complex *Wn,char flag)
{
Wn->real = cos(2*PI*i/n);
if(flag == 1)
Wn->imag = -sin(2*PI*i/n);
else if(flag == 0)
Wn->imag = -sin(2*PI*i/n);
}
//傅立葉變化
void fft(int N,complex f[])
{
complex t,wn;//中間變數
int i,j,k,m,n,l,r,M;
int la,lb,lc;
/*----計算分解的級數M=log2(N)----*/
for(i=N,M=1;(i=i/2)!=1;M++);
/*----按照倒位序重新排列原訊號----*/
for(i=1,j=N/2;i<=N-2;i++)
{
if(i<j)
{
t=f[j];
f[j]=f[i];
f[i]=t;
}
k=N/2;
while(k<=j)
{
j=j-k;
k=k/2;
}
j=j+k;
}
/*----FFT演演算法----*/
for(m=1;m<=M;m++)
{
la=pow(2,m); //la=2^m代表第m級每個分組所含節點數
lb=la/2; //lb代表第m級每個分組所含碟形單元數
//同時它也表示每個碟形單元上下節點之間的距離
/*----碟形運算----*/
for(l=1;l<=lb;l++)
{
r=(l-1)*pow(2,M-m);
for(n=l-1;n<N-1;n=n+la) //遍歷每個分組,分組總數為N/la
{
lc=n+lb; //n,lc分別代表一個碟形單元的上、下節點編號
Wn_i(N,r,&wn,1);//wn=Wnr
c_mul(f[lc],wn,&t);//t = f[lc] * wn複數運算
c_sub(f[n],t,&(f[lc]));//f[lc] = f[n] - f[lc] * Wnr
c_plus(f[n],t,&(f[n]));//f[n] = f[n] + f[lc] * Wnr
}
}
}
}
//傅立葉逆變換
void ifft(int N,complex f[])
{
int i=0;
conjugate_complex(N,f,f);
fft(N,f);
conjugate_complex(N,f,f);
for(i=0;i<N;i++)
{
f[i].imag = (f[i].imag)/N;
f[i].real = (f[i].real)/N;
}
}
struct compx EE(struct compx b1,struct compx b2)
{
struct compx b3;
b3.real = b1.real*b2.real-b1.imag*b2.imag;
b3.imag = b1.real*b2.imag+b1.imag*b2.real;
return (b3);
}
void FFT(struct compx *xin,int N)
{
int f,m,LH,nm,i,k,j,L;
double p , ps ;
int le,B,ip;
float pi;
struct compx w,t;
LH=N/2;
f=N;
for(m=1;(f=f/2)!=1;m++){;} /*2^m=N*/
{
for(L=m;L>=1;L--) /*這裡和時域的也有差別*/
{
le=pow(2,L);
B=le/2; /*每一級碟形運算間隔的點數*/
pi=3.14159;
for(j=0;j<=B-1;j++)
{
p=pow(2,m-L)*j;
ps=2*pi/N*p;
w.real=cos(ps);
w.imag=-sin(ps);
for(i=j;i<=N-1;i=i+le)
{
ip=i+B;
t=xin[i];
xin[i].real=xin[i].real+xin[ip].real;
xin[i].imag=xin[i].imag+xin[ip].imag;
xin[ip].real=xin[ip].real-t.real;
xin[ip].imag=xin[ip].imag-t.imag;
xin[ip]=EE(xin[ip],w);
}
}
}
}
/*變址運算*/
nm=N-2;
j=N/2;
for(i=1;i<=nm;i++)
{
if(i<j){t=xin[j];xin[j]=xin[i];xin[i]=t;}
k=LH;
while(j>=k){j=j-k;k=k/2;}
j=j+k;
}
}
FFT.H
#ifndef __FFT_H__
#define __FFT_H__
typedef struct complex //複數型別
{
float real; //實部
float imag; //虛部
}complex;
struct compx
{
double real;
double imag;
};
#define PI 3.1415926535897932384626433832795028841971
///
void conjugate_complex(int n,complex in[],complex out[]);
void c_plus(complex a,complex b,complex *c);//複數加
void c_mul(complex a,complex b,complex *c) ;//複數乘
void c_sub(complex a,complex b,complex *c); //複數減法
void c_div(complex a,complex b,complex *c); //複數除法
void fft(int N,complex f[]);//傅立葉變換 輸出也存在陣列f中
void ifft(int N,complex f[]); // 傅立葉逆變換
void c_abs(complex f[],float out[],int n);//複數陣列取模
void FFT(struct compx *xin,int N);
#endif
main.c
程式是根據網上的程式更改參考的,用的是別人自己寫的FFT,把兩個人寫的放到了一起,大家可以根據需要自己選擇如何呼叫,後面會更新使用官方庫版本的FFT的程式碼版本。串列埠部分就使用串列埠1就行,如果是正點的板子程式改寫是預設開啟了串列埠1的。
/* Includes ------------------------------------------------------------------*/
#include "main.h"
#include "usart.h"
#include "fft.h"
#include <math.h>
/* Private typedef -----------------------------------------------------------*/
/* Private define ------------------------------------------------------------*/
/* Private macro -------------------------------------------------------------*/
#define N 1024 //取樣點數
#define Fs 10240 //取樣頻率
#define F 10 //解析度
/* Private variables ---------------------------------------------------------*/
/* Private function prototypes -----------------------------------------------*/
/* Private functions ---------------------------------------------------------*/
//FFT測試資料集 輸入陣列
complex FFT_256PointIn[N];
//FFT測試資料集 輸出陣列
float FFT_256PointOut[N/2];
//填入陣列
double result[N];
struct compx s[N];
void InitBufInArray()
{
unsigned short i;
for(i=0; i<N; i++)
{
FFT_256PointIn[i].real = 1 * sin(2*PI * i * 1000.0 / Fs)
+1;
FFT_256PointIn[i].imag = 0;
}
}
/******************************************************************
函數名稱:GetPowerMag()
函數功能:計算各次諧波幅值
引數說明:
備 注:先將FFT_256PointIn分解成實部(X)和虛部(Y),
然後計算幅值:(sqrt(X*X+Y*Y)*2/N
然後計算相位:atan2(Y/X)
*******************************************************************/
void GetPowerMag()
{
unsigned short i;
float X,Y,P,Mag;
c_abs(FFT_256PointIn,FFT_256PointOut,N/2);
for(i=0; i<N/2; i++)
{
X = FFT_256PointIn[i].real/N; //計算實部
Y = FFT_256PointIn[i].imag/N; //計算虛部
Mag = FFT_256PointOut[i]*2/N; //計算幅值
P = atan2(Y,X)*180/PI; //計算相位
printf("%d ",i);
printf("%d ",F*i);
printf("%f \r\n",Mag);
// printf("%f ",P);
// printf("%f ",X);
// printf("%f \r\n",Y);
}
}
void dsp_g2_test()
{
u16 i=0;
for(i=0;i<N;i++)
{
s[i].real = 32000 * sin(PI*2*i*(50.0f/Fs));
s[i].real+= 16000 * sin(PI*2*i*(550.0f/Fs));
s[i].real+= 9000 * sin(PI*2*i*(1150.0f/Fs));
s[i].real+= 6000 * sin(PI*2*i*(2100.0f/Fs));
s[i].real+= 4000 * sin(PI*2*i*(5000.0f/Fs));
s[i].imag=0;
}
FFT(s,N);
for(i=0;i<N/2;i++)
{
if(i==0)
result[i] = sqrt(s[i].real * s[i].real + s[i].imag * s[i].imag)/N;
else
result[i] = sqrt(s[i].real * s[i].real + s[i].imag * s[i].imag)*2/N;
printf("%d ",i);
printf("%d ",10*i);
printf("%f \r\n",result[i]);
//if(result[i] > 10)
//printf("%4d,%4d,%ld\n",i,(u16)((double)i*Fs/NPT),(u32)result[i]);
}
}
/**
* @brief 串列埠列印輸出
* @param None
* @retval None
*/
int main(void)
{
int i,t;
SystemInit();//系統時鐘初始化
USART_Configuration();//串列埠1初始化
printf("這是一個FFT 測試實驗\r\n");
InitBufInArray();
fft(N,FFT_256PointIn);
printf("點數 頻率 幅值 實部 虛部\n");
//GetPowerMag();
dsp_g2_test();
while(1)
{
//檢查接收資料完成標誌位是否置位
if(USART_GetFlagStatus(USART1, USART_IT_RXNE) != RESET)
{
//將接收到的資料傳送出去,對USART_DR的讀操作可以將USART_IT_RXNE清零。
printf("%c",USART_ReceiveData(USART1));
}
}
}
/*********************************END OF FILE**********************************/
串列埠的截圖結果是正確的。

免費開源,大家參考,不通過csdn騙積分了,如果有點收穫希望能給個關注和點贊。
工程連結