這學期上數學課時老師佈置了一道習題：計算勒讓德多項式的模。翻看本科數學物理方法教材，發現計算方法較複雜，且用到了生成函數
為了方便理清整個計算過程，這一部落格直接從羅德里格斯公式出發並避免使用其它引論，或許對初次學習特殊函數有所幫助

羅德里格斯公式

勒讓德多項式的一個重要物理背景就是球座標下的靜電場滿足的拉普拉斯方程，${\nabla }^{2}V=0$，即
$$r^{-2}{\partial }_r^2(r^{2}V)+r^{-2}(sin(\theta ){)}^{-1}{\partial }_{\theta }^{2}V+r^{-2}(sin(\theta ){)}^{-2}{\partial }_{\varphi }^{2}V=0$$
分離變數：$V=R(r)\Theta (\theta )\Phi (\varphi )$，得$\Theta$滿足得常微分方程為：
$$\frac{1}{sin\theta }\frac{d}{d\theta }\left(sin\theta \frac{d\Theta }{d\theta }\right)+l(l+1)\Theta -\frac{m^2}{si{n}^2\theta }\Theta =0$$.
進行變數代換：$x=cos(\theta ),dx=-sin\theta d\theta$，並假定$m=0$，即得到勒讓德方程：
$$\frac{d}{dx}((1-u^2)\frac{d\Theta }{dx})+l(l+1)\Theta =0,x\in [-1,1]$$
該方程可通過級數法求解，所得級數與由羅德里格斯公式：
$$P_l(x)=\frac{1}{2^{l}l!}{u}_l^{(l)}(x),u_l(x)=(x^2-1{)}^l$$
展開後相同（參考數學物理方法教材）。
由於$u_l(x)$為2n次多項式，因此求$l$次導後所得$P_l(x)$為$l$次多項式，且前幾階勒讓德多項式為：
$$P_0(x)=1,P_1(x)=x,P_2(x)=\frac{1}{2}(3x^2-1)$$

正交性

正交性即證明$⟨P_m,P_n⟩={\int }_{-1}^1{P}_m(x)P_n(x)dx=0,m\ne n$.
設$m>n\ge 0$，則$P_n(x)$為n次多項式，因此只需證明對任意$k\le n$，均有${\int }_{-1}^1{P}_m(x)x^{k}dx=0$.

1. 對於$k=0$，有：
   $${\int }_{-1}^1{P}_m(x)dx=\frac{1}{2^{m}m!}{u}_m^{(m-1)}{|}_{-1}^1$$
   而對任意$m^{\prime }<m$，由萊布尼茲公式：
   $$u_m^{(m^{\prime })}=\sum _{m^{\prime \prime }=0}^{m^{\prime }}[(x+1{)}^m{]}^{(m^{\prime \prime })}[(x-1{)}^m{]}^{(m^{\prime }-m^{\prime \prime })}$$
   由於$m^{\prime \prime },m^{\prime }-m^{\prime \prime }<m$
   $$u_m^{(m^{\prime })}(1)=u_m^{(m^{\prime })}(-1)=0$$
   （注意當$m^{\prime }=0$時上式同樣成立）
   因此，${\int }_{-1}^1{P}_m(x)dx=0$
2. 對於$k\ge 1$，使用分部積分：
   $${\int }_{-1}^1{P}_m(x)x^{k}dx=\frac{1}{2^{m}m!}\left(x^k{u}_m^{(m-1)}{|}_{-1}^1-k{\int }_{-1}^1{u}_m^{(m-1)}(x)x^{k-1}dx\right)$$
   其中第一項為0，重複使用分部積分，最終得到：
   $$\begin{gathered} {\int }_{-1}^1{P}_m(x)x^{k}dx=\frac{(-1{)}^{k}k!}{2^{m}m!}{\int }_{-1}^1{u}_m^{(m-k)}(x)dx \\ =u_m^{(m-k-1)}{|}_{-1}^1=0 \end{gathered}$$

正交性得證；

歸一化

勒讓德多項式的模為：
$$\Vert P_n{\Vert }_{L^2}=\sqrt{{\int }_{-1}^1{P}_n(x)P_n(x)dx}$$
當$n=0$，有$\Vert P_0{\Vert }_{L^2}=\sqrt{2}$
當$n\ge 1$，有：
$$\begin{gathered} {\int }_{-1}^1{P}_n(x)P_n(x)dx=\frac{1}{(2^{n}n!{)}^2}{\int }_{-1}^1{u}_n^{(n)}(x)u_n^{(n)}(x)dx \\ =\frac{1}{(2^{n}n!{)}^2}\left(u_n^{(n)}{u}_n^{(n-1)}{|}_{-1}^1-{\int }_{-1}^1{u}_n^{(n-1)}(x)u_n^{(n+1)}(x)dx\right) \\ =\frac{(-1{)}^n}{(2^{n}n!{)}^2}{\int }_{-1}^1{u}_n(x)u_n^{(2n)}(x)dx \end{gathered}$$
由於$u_n$最高次項為$x^{2n}$，$u_n^{(2n)}(x)=(2n)!$。令 $I_n={\int }_{-1}^1{u}_n(x)dx$，使用分部積分：
$$I_n=x{u}_n{|}_{-1}^1-2n{\int }_{-1}^1{x}^2(x^2-1{)}^{n-1}dx=-2n{I}_n-2n{I}_{n-1}$$
移項，並重復這一步驟，可得：
$$I_n=\frac{(-1{)}^n{\prod }_{k=1}^n(2k)}{{\prod }_{k=1}^n(2k+1)}{I}_0$$
而$I_0=2$,於是，勒讓德多項式模為：
$$\Vert P_0{\Vert }_{L^2}=\sqrt{\frac{(-1{)}^n(2n)!}{(2^{n}n!{)}^2}\frac{2(-1{)}^n{\prod }_{k=1}^n(2k)}{{\prod }_{k=1}^n(2k+1)}}=\sqrt{\frac{2}{2n+1}}$$
歸一化的勒讓德多項式即為：
$$Q_n=\sqrt{\frac{2n+1}{2}}{P}_n$$

應用

由維爾斯特拉斯定理，任意閉區間上連續函數$f$可用某一多項式逼近，而這一多項式就可表示為勒讓德多項式之和：
$$p(x)=\sum _{n=0}^{\infty }⟨Q_n,f⟩Q_n$$

與泰勒展開不同，這裡未假設連續函數$f$可導。
作為例子，設
$$f(x)=tri(2x-1),x\in [-1,1]$$
將該函數展開到不同階，如圖所示

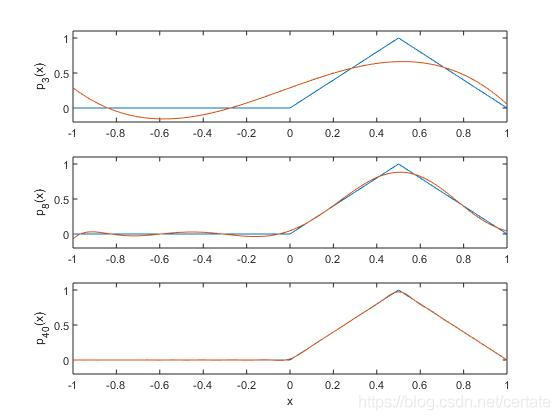
程式碼如下：

x=-1:.01:1;
len=length(x);
f_0=@f0;
coef(f_0,0)
subplot(3,1,1)
p_n=zeros(1,len);
for n=0:3
   p_n=p_n+coef(f_0,n)*Q(x,n,0);
end
plot(x,f0(x),x,p_n),axis([-1,1,-0.2,1.1])
ylabel('p_3(x)')

subplot(3,1,2)
for n=4:8
   p_n=p_n+coef(f_0,n)*Q(x,n,0);
end
plot(x,f0(x),x,p_n),axis([-1,1,-0.2,1.1])
ylabel('p_{8}(x)')

subplot(3,1,3)
for n=9:40
   p_n=p_n+coef(f_0,n)*Q(x,n,0);
end
plot(x,f0(x),x,p_n),axis([-1,1,-0.2,1.1])
ylabel('p_{40}(x)')
xlabel('x')

function f=f0(x)
n=length(x);
temp=zeros(1,n);
for i=1:n
if x(i)>0&&x(i)<1
   temp(i)=1-abs(2*(x(i)-1/2));
end
end
f=temp;
end

function f=coef(f0,n)
p_f0=@(x)(f0(x).*Q(x,n,0));
f=integral(p_f0,-1,1);
end

function f=Q(x,n,m)
temp=legendre(n,x);
f=sqrt((2*n+1)/2)*temp(m+1,:);
end

在求解電磁波散射問題時，就可以在球座標下將入射場展開為勒讓德多項式，並將散射場展開而其係數待定，再通過邊界條件求得散射場展開係數。

參考：汪德新，數學物理方法