二補數的由來
前言
一般來說,進行10進位制的運算 14 − 14 = 0 14-14=0 14−14=0,這是小學二年級就能口算出來的,那麼計算機內部是如何處理的呢?計算機進行加法運算的時候,將原碼進行相加即可得到正確的結果,那麼 14 − 14 14-14 14−14直接進行原碼的操作會發生什麼呢?
14 D = 00001110 B 14D = 00001110B 14D=00001110B − 14 D = 10001110 B -14D = 10001110B −14D=10001110B
我們知道
14
−
14
=
14
+
(
−
14
)
14-14 = 14+(-14)
14−14=14+(−14),計算一下得知
0
0
0
0
1
1
1
0
+
1
0
0
0
1
1
1
0
1
0
0
1
1
1
0
0
\begin{matrix} &0&0&0&0&1&1&1&0\\ +&1&0&0&0&1&1&1&0\\ \hline &1&0&0&1&1&1&0&0\\ \end{matrix}
+011000000001111111110000
那麼此時的有符號二進位制數 10011100 B = − 28 D 10011100B=-28D 10011100B=−28D,計算結果是-28,這顯然不符合我們的預期。
老師們通常的教法
老師們通常引導我們用的是生活中時鐘的例子
假如現在的時間是10點,並且假如我們的鐘錶快了2小時,那麼我們最容易想到的辦法就是往回倒走2小時,我們通常會想到的算式是 10 − 2 = 8 10 - 2 = 8 10−2=8,另外一種笨的辦法就是讓他走快一些,快多少呢,我們需要撥快的時間是 12 − 2 = 10 12-2=10 12−2=10小時
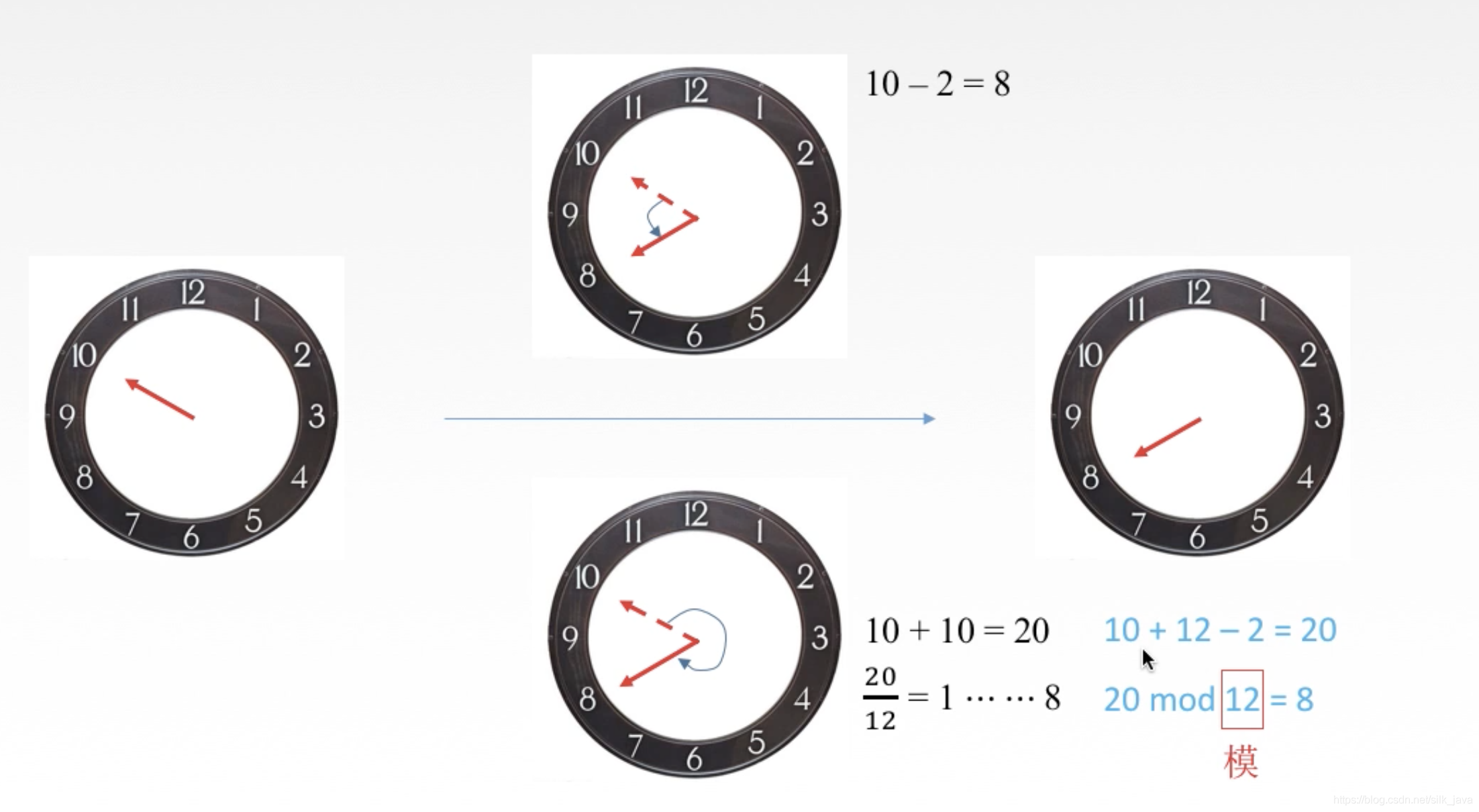
我們需要將時鐘撥快10個小時 10 + 10 = 20 10+10=20 10+10=20,撥快10小時後時間變為了20點,因為時鐘一圈的總數是12,所以超過20是沒有意義的,那麼就要減去12,那麼此處為什麼要取模運算呢,因為可能超過12的數量可以是很多很多圈,例如超過了2個12小時 ,那麼此時就需要減去24小時。
由此我們得出的結論是:
在時鐘這個問題上,要想將10點變為8點,用 10 + ( − 2 ) 10+(-2) 10+(−2)和用 10 + ( 12 − 2 ) = 10 + 10 10+(12-2)=10+10 10+(12−2)=10+10的效果是一樣的,由此,我們延伸一下,我們感覺在一個有周期性的事物當中,有時候加上一個負數等於加上這個週期減去這個負數的絕對值。
我們來看下下面的推算過程,我們最開始是希望這樣的運算
0
0
0
0
1
1
1
0
+
1
0
0
0
1
1
1
0
1
0
0
1
1
1
0
0
\begin{matrix} &0&0&0&0&1&1&1&0\\ +&1&0&0&0&1&1&1&0\\ \hline &1&0&0&1&1&1&0&0\\ \end{matrix}
+011000000001111111110000
因為有符號位,我們計算的結果是錯誤的,所以我們希望轉化為兩個無符號的數位,通過上面的分析,我們希望轉化為下面
0
0
0
0
1
1
1
0
−
0
0
0
0
1
1
1
0
0
0
0
0
0
0
0
0
\begin{matrix} &0&0&0&0&1&1&1&0\\ -&0&0&0&0&1&1&1&0\\ \hline &0&0&0&0&0&0&0&0\\ \end{matrix}
−000000000000110110110000
此時去掉了符號位,如果直接相減,得到的結果0就是我們想要的結果,但是此時需要計算機實現符號位的自動處理,這在實現上會很複雜,但是通過上面的分析,我們知道任何數位加上它的模之後都還等於它自身的值,於是我們可以利用加法的交換率進行推導,當然前提是字長為8的計算機數
−
14
D
=
−
14
D
+
256
D
=
−
00001110
B
+
10000000
B
=
+
10000000
B
−
00001110
B
-14D=-14D+256D=-00001110B+10000000B=+10000000B-00001110B
−14D=−14D+256D=−00001110B+10000000B=+10000000B−00001110B
於是我們可以得到下面的式子:
0
0
0
0
1
1
1
0
+
1
0
0
0
0
0
0
0
0
−
0
0
0
0
1
1
1
0
\begin{matrix} &&&&&&&&&&&0&0&0&0&1&1&1&0\\ +&1&0&0&0&0&0&0&0&0&-&0&0&0&0&1&1&1&0\\ \hline \end{matrix}
+100000000−0000000011111100
因為
256
=
1
+
255
256=1+255
256=1+255,所以可以繼續演化為:
0
0
0
0
1
1
1
0
+
(
0
0
0
0
0
0
0
1
+
0
1
1
1
1
1
1
1
)
−
1
0
0
0
1
1
1
0
\begin{matrix} &&&&&&&&&&&&&&&&&&&&&0&0&0&0&1&1&1&0\\ +&(&0&0&0&0&0&0&0&1&+&0&1&1&1&1&1&1&1&)&-&1&0&0&0&1&1&1&0\\ \hline \end{matrix}
+(00000001+01111111)−0100000011111100
此時利用加法的運算優先順序相同的原則,繼續演化為
0
0
0
0
1
1
1
0
+
0
0
0
0
0
0
0
1
+
(
0
1
1
1
1
1
1
1
−
1
0
0
0
1
1
1
0
)
\begin{matrix} &&&&&&&&&&&&&&&&&&&&&0&0&0&0&1&1&1&0\\ +&0&0&0&0&0&0&0&1&+&(&0&1&1&1&1&1&1&1&&-&1&0&0&0&1&1&1&0&)\\ \hline \end{matrix}
+00000001+(01111111−0100000011111100)
我們一系列的推導,其實就是下面的式子
100000000 − 00001110 = ( 00000001 + 01111111 ) − 10001110 = 00000001 + ( 01111111 − 10001110 ) = 11110010 100000000-00001110 = (00000001+01111111)-10001110 = 00000001+(01111111-10001110) = 11110010 100000000−00001110=(00000001+01111111)−10001110=00000001+(01111111−10001110)=11110010
如果我們先計算括號中的式子就會發現奇蹟,得到的數位就是-14的按位元取反,即每一個位元上面的數位除了符號位的全部數值位取反,那麼最後再加上最前面的1,我們可以得到如下的式子
0 0 0 0 1 1 1 0 + 1 1 1 1 0 0 1 0 1 0 0 0 0 0 0 0 \begin{matrix} &0&0&0&0&1&1&1&0\\ +&1&1&1&1&0&0&1&0\\ \hline &1&0&0&0&0&0&0&0\\ \end{matrix} +011010010010100100110000
此時我們進行取模運算 100000000 / 256 = 0 100000000/256=0 100000000/256=0,其實不進行取模運算的話,對於字長為8的有符號二進位制數位來說,一個位元組的長度只有8位元,最高位的1已經被捨棄了,式子的結果還是等於0,於是我們實現了 14 + ( − 14 ) 14+(-14) 14+(−14)的機器運算的正確結果,此時回憶一下這個式子我們做了什麼
- 把一個負數a等價換算為 a + 模 a+模 a+模,(也有說用模減去這個數的相反數的,即: a = m o d − ∣ a ∣ a=mod-|a| a=mod−∣a∣),即 a + 100000000 a+100000000 a+100000000,例如
− 14 = − 14 + 256 = 256 − 14 -14=-14+256=256-14 −14=−14+256=256−14
- 把模換算成1+2n-1,例如
256 = 1 + 255 256=1+255 256=1+255,即100000000 等=00000001+01111111
- 優先計算 01111111 − a 01111111-a 01111111−a,此時得到的結果是a的按位元取反的值,即反碼
- 加上最前面的數位00000001,即再加上1
於是我們把這一系列的過程得到的機器碼叫做二補數,並且知道了,二補數的機器碼等於按位元取反之後,再加上數位1,這一系列的操作可以用下面的這幅圖來表示
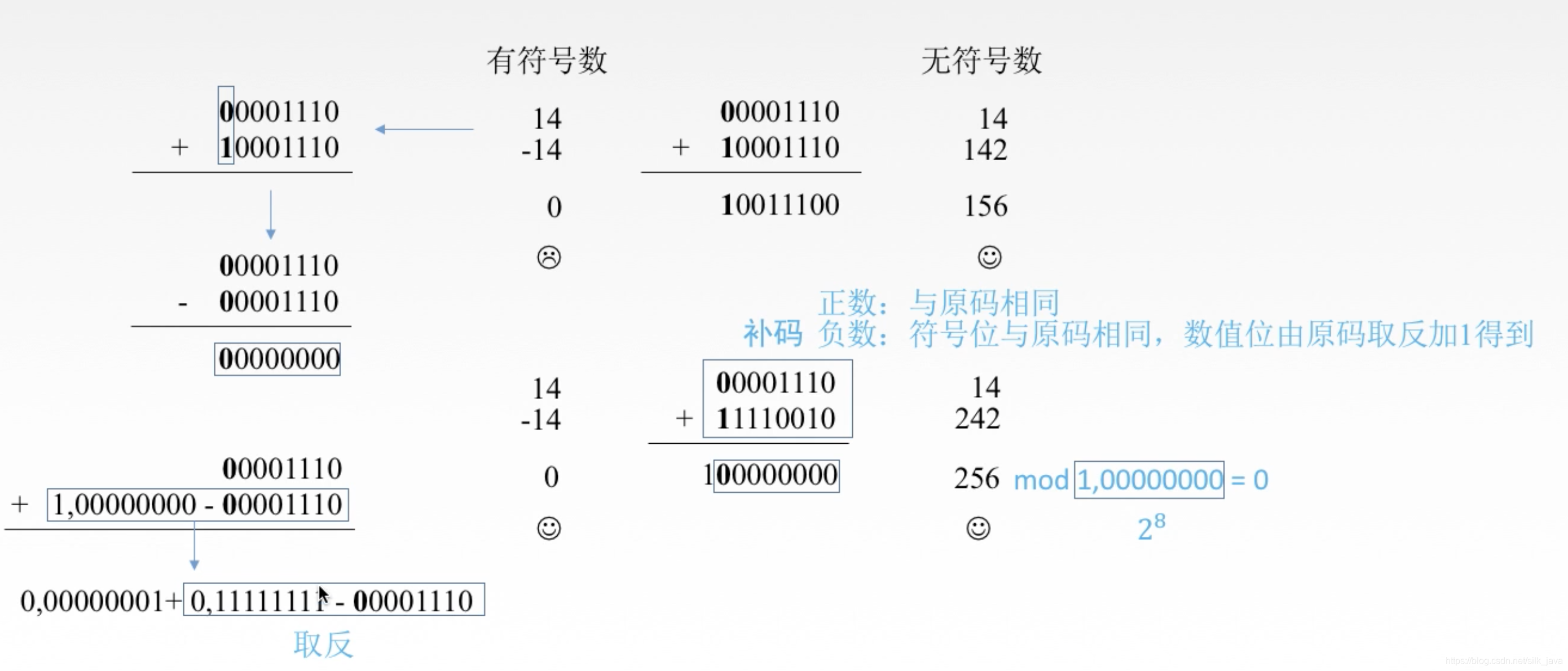
這其中,我們經歷了數位的拆分,運算的優先順序變化,就像小學時候的快速運演演算法( 9 + 6 + 4 = ? 9+6+4=? 9+6+4=?,我們就會先運算 6 + 4 6+4 6+4),至此我們明白了為什麼負數的反碼等於按位元取反之後再加上1了。
我自己更能理解的方法
其實我們完全可以忘掉上面的時鐘,我們想象一下每天有256個小時,那麼我們的鐘表是這樣的,我認為這樣更好理解一些。假如現在是192點,但是實際上鐘錶快了64個小時,為了將時鐘調整準確,接下來看下面的 這個圖
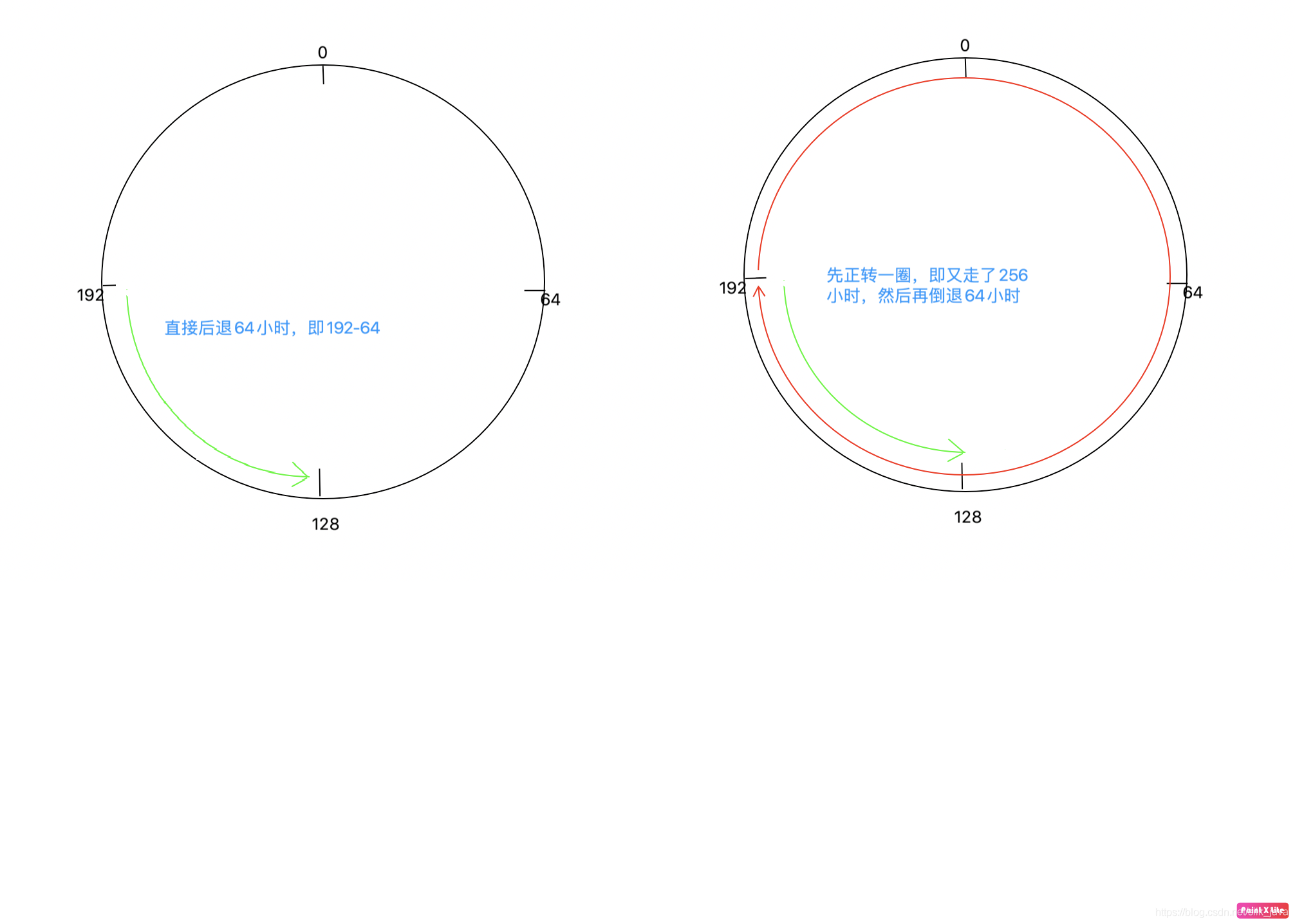
192 − 64 192-64 192−64
192 + 256 − 64 192+256-64 192+256−64
我們知道這兩個式子的計算結果都是可以把時鐘調整到我們想要的結果,也就是結果是相等的,於是就按照第二個式子進行做吧
192
+
256
−
64
=
192
+
(
256
−
64
)
=
192
+
(
1
+
255
−
64
)
=
192
+
(
1
+
(
255
−
64
)
)
192+256-64 = 192+(256-64) =192+(1+255-64) = 192+(1+(255-64))
192+256−64=192+(256−64)=192+(1+255−64)=192+(1+(255−64))
我們換成二進位制的計其數的寫法,應該是這樣的
1 1 0 0 0 0 0 0 + 1 0 0 0 0 0 0 0 0 − 0 1 0 0 0 0 0 0 \begin{matrix} &&&&&&&&&&&1&1&0&0&0&0&0&0\\ +&1&0&0&0&0&0&0&0&0&-&0&1&0&0&0&0&0&0\\ \hline \end{matrix} +100000000−1011000000000000
1 1 0 0 0 0 0 0 + 0 0 0 0 0 0 0 1 + 0 1 1 1 1 1 1 1 − 0 1 0 0 0 0 0 0 \begin{matrix} &&&&&&&&&&&&&&&&&&&1&1&0&0&0&0&0&0\\ +&0&0&0&0&0&0&0&1&+&0&1&1&1&1&1&1&1&-&0&1&0&0&0&0&0&0\\ \hline \end{matrix} +00000001+01111111−1011000000000000
1 1 0 0 0 0 0 0 + 0 0 0 0 0 0 0 1 + ( 0 1 1 1 1 1 1 1 − 0 1 0 0 0 0 0 0 ) \begin{matrix} &&&&&&&&&&&&&&&&&&&&1&1&0&0&0&0&0&0\\ +&0&0&0&0&0&0&0&1&+&(&0&1&1&1&1&1&1&1&-&0&1&0&0&0&0&0&0&)\\ \hline \end{matrix} +00000001+(01111111−1011000000000000)
1 1 0 0 0 0 0 0 + 0 0 0 0 0 0 0 1 + 0 0 1 1 1 1 1 1 \begin{matrix} &&&&&&&&&&1&1&0&0&0&0&0&0\\ +&0&0&0&0&0&0&0&1&+&0&0&1&1&1&1&1&1\\ \hline \end{matrix} +00000001+1010010101010101
1
1
0
0
0
0
0
0
+
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
\begin{matrix} &1&1&0&0&0&0&0&0\\ +&0&1&0&0&0&0&0&0\\ \hline &1&0&0&0&0&0&0&0\\ \end{matrix}
+101110000000000000000000
10000000B=128,此時,時鐘又回到了128點,我們的結果正確了。
結論
- 對於正數來說
原碼=反碼=二補數
這是我們一眼就能看懂的有符號機器數
- 對於負數來說
反 碼 = 原 碼 的 符 號 位 不 變 , 數 值 位 按 位 取 反 反碼 = 原碼的符號位不變,數值位按位元取反 反碼=原碼的符號位不變,數值位按位取反
補 碼 = 原 碼 的 符 號 位 不 變 , 數 值 位 按 位 取 反 , 然 後 + 1 二補數 = 原碼的符號位不變,數值位按位元取反,然後+1 補碼=原碼的符號位不變,數值位按位取反,然後+1
補 碼 = 負 數 + 模 = 模 − 負 數 的 絕 對 值 , 二補數 = 負數+模=模-負數的絕對值, 補碼=負數+模=模−負數的絕對值,這一點很重要,因為原碼的符號位不變,數值位按位元取反,然後+1這個結論就是通過二補數=模-負數的絕對值演算過來的
為什麼二補數的二補數是原碼
前面我們得到了結論
二補數 = 原碼的符號位不變,數值位按位元取反,然後+1
那麼我們現在把二補數再求一下二補數,就是求二補數的二補數,我們以-14為例
- -14的原碼[-14D]原=10001110B
- 先求出-14的反碼 [-14]反 = 11110001
- 再求出二補數 [-14]補 = 11110010
- 此時我們求出二補數的反碼, [[-14]補 ]反 =10001101
- 再求出二補數的二補數[[-14]補 ]補 =10001110
可以看出10001110和[-14]相等,即[[-14]補 ]補=[-14D]原,也就是原碼的二補數的二補數=原碼,這是一種巧合嗎,如何證明,其實很簡單
我們不用去管什麼取反加1這些概念,而是從二補數的由來說起
假設一個負數是a,那麼它的[a]補=a+模=模-(-a),那麼[[a]補]補=模-(模-(-a))=模-模+a=a,於是就等於它自身了