基於FPGA的SNR噪聲分析

    對於移相波束形成的抗噪聲效能分析，我們主要通過對系統在不同的SNR訊雜比下進行模擬分析。這裡FPGA的幾個主要模擬引數：入射角為5度，FFT變換長度為256，將FPGA系統分別在沒有噪聲，SNR為-10db，SNR為0db，SNR為10db三種情況對比沒有噪聲下的模擬結果。

    通過模擬，我們可以得到如下的模擬結果：

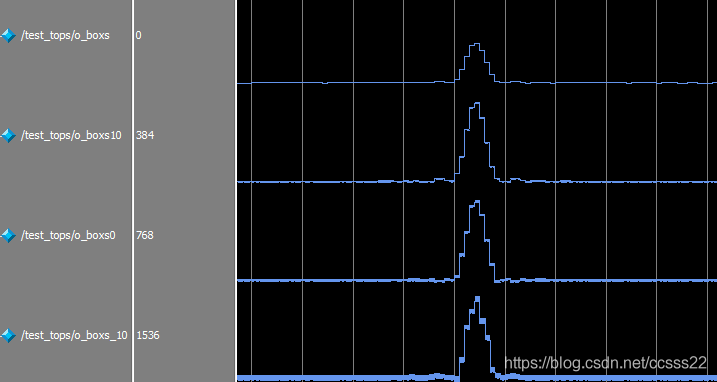
圖1 不同SNR下波束形成模擬結果

    圖1的模擬結果中，o_boxes為沒有噪聲的波束形成，o_boxes10為訊雜比為10db下的波束形成輸出，o_boxes0為訊雜比為0db下的波束形成輸出，o_boxes_10為訊雜比為-10db下的波束形成輸出。從上面的模擬結果可以看到，當噪聲不斷增加的時候，輸出的波束形成具有明顯的噪聲干擾。

    上圖是入射角為5度的時候模擬。為了進一步對比噪聲對角度計算的精度影響，將上面的模擬圖放大，可以看到如下的模擬結果圖。

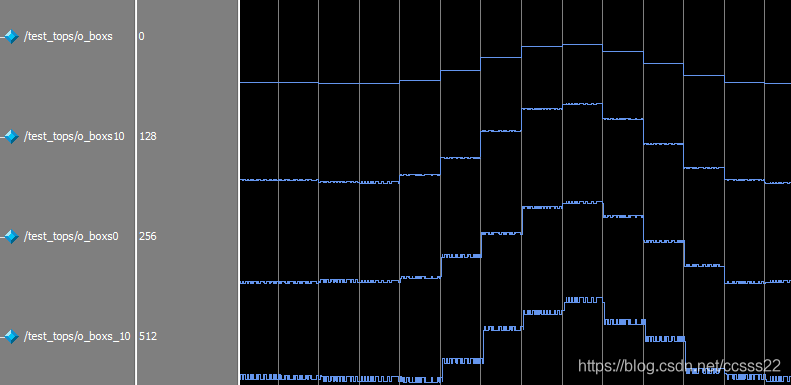
圖2不同SNR下波束形成放大後的模擬結果

    從圖2的模擬結果可以看到，我們以不帶噪聲的輸出作為標準的角度值，當SNR為10db的時候，誤差在0.02度左右，當SNR為0db的時候，誤差在0.04度左右，當SNR為-10db的時候，誤差在0.07度左右。

    從上面的模擬結果可以看到，隨著噪聲功率的增加，移相波束形成得到的角度計算值誤差越大，對比本文前面章節的MATLAB模擬結果可知，最後計算的角度存在一定的誤差。

    計算結論基本能夠反映實際的噪聲影響，和MATLAB的理論模擬結果誤差是因為在FPGA設計過程中，每一個模組都需要擷取位寬以及量化處理，因此會存在較大的誤差。當做乘法運算的時候，資料的位寬會翻倍的增加，如果不進行位寬的擷取，則會大大增加FPGA內部的資源佔用，因此一般情況下，每次做完乘法運算，往往需要進行位寬的擷取，擷取位寬導致的誤差取決於位寬擷取的大小，位寬擷取越多，則誤差越大，位寬擷取越少，則誤差越小。

    另外一方面，由於在FPGA內部採用的計算方法是定點計算方法，這會引入量化噪聲，由量化噪聲導致的誤差稱為量化誤差量化誤差是指量化結果和被量化模擬量的差值，顯然量化級數越多，量化的相對誤差越小。量化級數指的是將最大值均等的級數，每一個均值的大小稱為一個量化單位。

·基於FPGA的角度解析度分析

    通過輸入不同入射角的訊號，分別分析入射角的理論值和實際計算值的誤差。這裡，分別設定入射角為5度和15度，SNR訊雜比為10db，FFT傅立葉變換的長度設定為256，然後進行模擬，模擬結果如下所示：

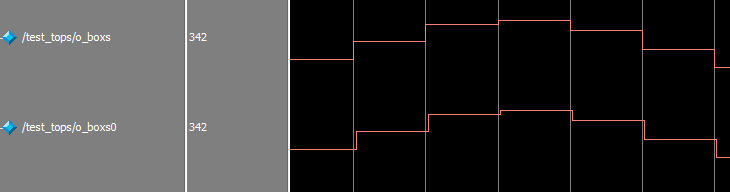
圖3 入射角為5度的模擬結果

圖3中第一個波形為理想狀態下的入射角，第二個圖為通過移相波束形成後的角度計算值，為了更精確的分析角度計算的精度，我們將輸出波形進行區域性的放大，得到如下的模擬結果圖。 

圖4 入射角為5度的模擬結果（區域性放大）

    從圖4的模擬結果可知，當入射角為5度的時候，其誤差在0.02度左右，這說明系統可以很好的達到測定目標方向的目標，其誤差在0.4%左右。

    為了更進一步的分析基於FPGA的移相波束形成的角度解析度，我們將入射角設定為15度，其餘引數和上面的引數相同，得到如下的模擬結果：

圖5 入射角為15度的模擬結果

    和圖3的模擬結果類似，圖5中第一個波形為理想狀態下的入射角，第二個圖為通過移相波束形成後的角度計算值，然後我們將輸出波形進行區域性的放大，得到如下的模擬結果圖。 

圖6 入射角為15度的模擬結果（區域性放大）

    從圖6的模擬結果可知，當入射角為15度的時候，其誤差在0.07度左右，雖然誤差角度大於入射角為5度的計算結果，但其誤差百分比為0.467%，基本和上面的模擬結果一直。

    通過上面兩種入射角情況下的輸入訊號計算結果的對比，最後得到的誤差結果基本和MATLAB的誤差結果一直。

    模擬得到的0.4%左右的誤差，主要來自三個方面的影響。

    第一，噪聲的干擾，由於模擬的時候引入了SNR=10db的噪聲，因此，最後的輸出結果會存在一定的誤差。

    第二，由於FPGA和位寬擷取和量化噪聲導致結論的誤差，這個原因和上一節介紹的原因類似。

    第三，FPGA系統內部時鐘及部分時序抖動而導致的誤差。