5537. 分割兩個字串得到迴文串

題目描述：

給你兩個字串 a 和 b ，它們長度相同。請你選擇一個下標，將兩個字串都在 相同的下標 分割開。由 a 可以得到兩個字串： aprefix 和 asuffix ，滿足 a = aprefix + asuffix ，同理，由 b 可以得到兩個字串 bprefix 和 bsuffix ，滿足 b = bprefix + bsuffix 。請你判斷 aprefix + bsuffix 或者 bprefix + asuffix 能否構成迴文串。

當你將一個字串 s 分割成 sprefix 和 ssuffix 時， ssuffix 或者 sprefix 可以為空。比方說， s = "abc" 那麼 "" + "abc" ， "a" + "bc" ， "ab" + "c" 和 "abc" + "" 都是合法分割。

如果 能構成迴文字串 ，那麼請返回 true，否則返回 false 。

請注意， x + y 表示連線字串 x 和 y 。

範例 1：

輸入：a = "x", b = "y"
輸出：true
解釋：如果 a 或者 b 是迴文串，那麼答案一定為 true ，因為你可以如下分割：
aprefix = "", asuffix = "x"
bprefix = "", bsuffix = "y"
那麼 aprefix + bsuffix = "" + "y" = "y" 是迴文串。

範例 2：

輸入：a = "ulacfd", b = "jizalu"
輸出：true
解釋：在下標為 3 處分割：
aprefix = "ula", asuffix = "cfd"
bprefix = "jiz", bsuffix = "alu"
那麼 aprefix + bsuffix = "ula" + "alu" = "ulaalu" 是迴文串。

提示：

1 <= a.length, b.length <= 105
a.length == b.length
a 和 b 都只包含小寫英文字母

解題思路：

1）、由於切分的下標是一致的，也就是說 aprefix.length() = bprefix.length() && asuffix.length() = bsuffix.length() ;
判斷的是 aprefix + bsuffix 或者 bprefix + asuffix 是否是迴文；

2）、分析如圖所示：（是否能夠相遇 即 start >= over）

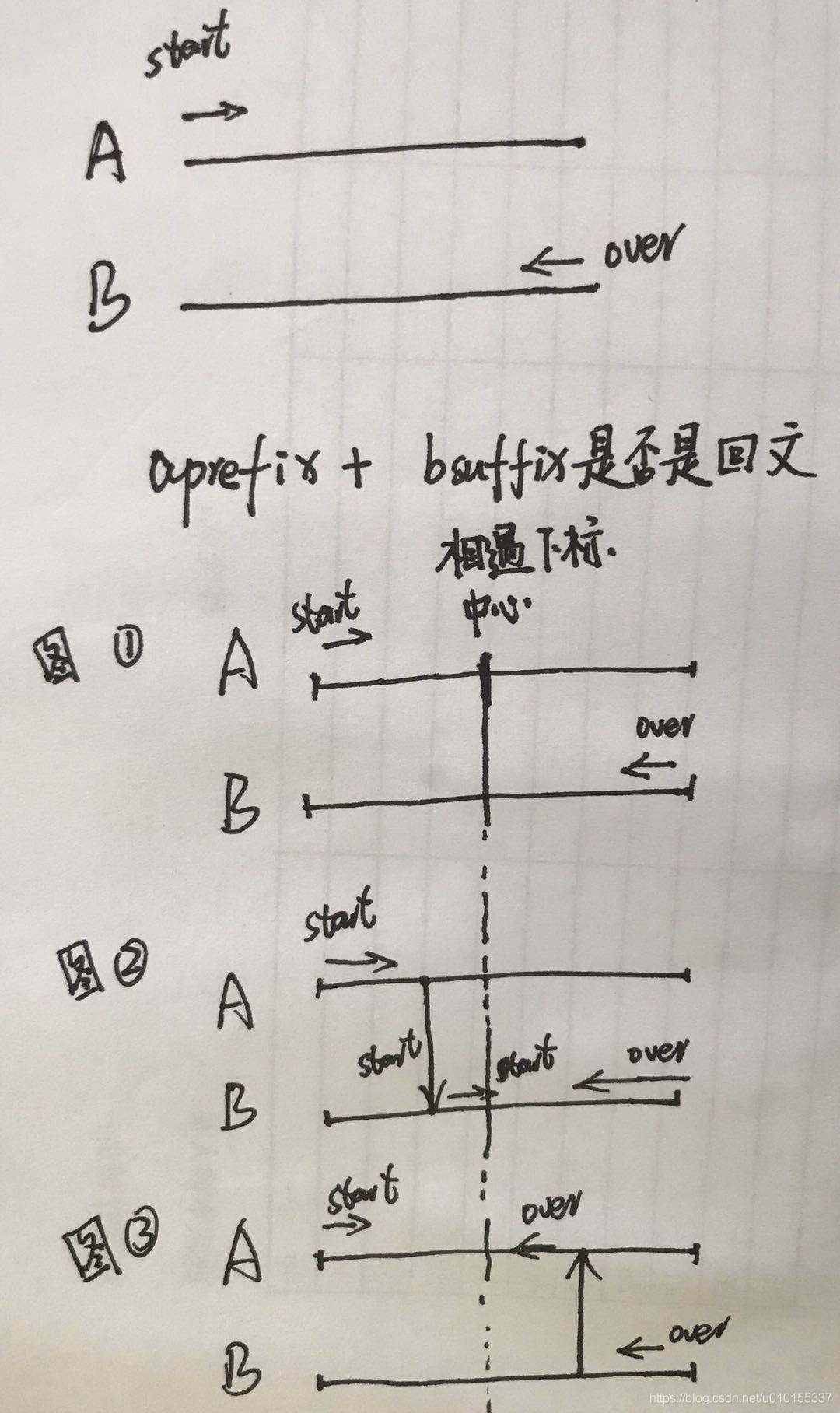
程式碼實現：

class Solution {
public:
// 判斷aprefix +  bsuffix 是否是迴文 ；
    bool getAnswer(string& a, string& b) {
        int start = 0 , over = a.length() - 1 , i  , j ;
        // 圖 1）
        while (start < over) {
            if (a[start] == b[over]) {
                start ++ ;
                over -- ;
            } else break ;
        }
        i = start , j = over ;
        // 圖 2）
        while (i < j) {
            if (b[i] == b[j]) {
                i ++ ;
                j -- ;
            } else break ;
        }
        if (i >= j) return true ;
        
        i = start , j = over ;
        // 圖 3）
        while (i < j) {
            if (a[i] == a[j]) {
                i ++ ;
                j -- ;
            } else break ;
        }
        if (i >= j) return true ;
        
        
        else return false ;
        
    }
    bool checkPalindromeFormation(string a, string b) {
        if (getAnswer(a , b) || getAnswer(b , a)) return true ;
        else return false ;
    }
};

複雜度計算：

時間複雜度：O(n) ；
空間複雜度：O(1) ；