技術文章 » 讀書筆記-增量學習-A CNN-Based Broad Learning System

讀書筆記-增量學習-A CNN-Based Broad Learning System

2020-10-12 16:00:36

一篇2018年關於基於CNN的增量學習論文：A CNN-Based Broad Learning System。

對計算機視覺來說，作者提出的CNN-Based Broad Learning System（CNNBLS）比 Broad Learning System（BLS）更有效。其中用折積層和最大池化層提取特徵，用principal component analysis（PCA） 主成分分析法對特徵降維，最後使用Ridge regression嶺迴歸法得到分類結果。

與BLS和RVFLNN相似，作者提出的CNNBLS中折積層的引數是隨機初始化的。同時，CNNBLS使用所有輸入資料做特徵提取，從而避免像BLS降維丟失細節資訊的問題。

在BLS中，輸入的高維資料首先會隨機對映到低維的x，再用x生成enhancement nodes。使用陳俊龍教授提的三種演演算法實現增量學習(*陳俊龍教授關於BLS論文的讀書筆記傳送門)。而作者提出的CNNBLS結構如下圖所示：

                                                     

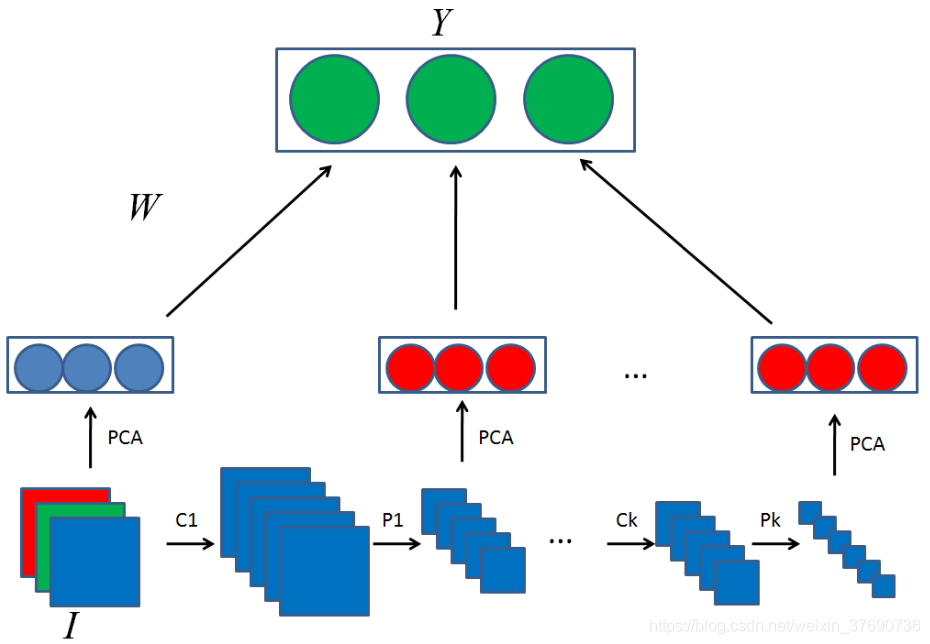
  1. 首先，像BLS一樣將輸入影象 I 對映到特徵向量 x 中。 不同之處在於，我們使用PCA學習對映矩陣，而BLS使用隨機投影。
  2. 然後，使用折積和池化操作將輸入影象 I 用於提取enhancement node增強節點。 PCA應用於池化層以提取enhancement feature增強特徵。
  3. 可以多次重複Step2以提取更深層的特徵。 其中折積核心是隨機生成的，嶺迴歸用於學習權重W。

虛擬碼如下：

                                                 

實驗中，作者採用控制變數測試如下引數對實驗結果的影響：

  1. N : 訓練樣本的數量，取值範圍 {500, 1000, 2000, 3000, 4000}
  2. P : PCA的引數，取值範圍 {0.91, 0.93, 0.95, 0.97, 0.99}
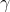  3. \gamma : 嶺迴歸的引數，取值範圍 {0.001, 0.01, 0.1, 1, 5, 10, 50, 100, 1000, 10000}
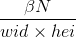
  4. 折積核心表示式為 : \frac{\beta N}{wid\times hei}
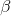  5. \beta : 取值範圍 {0.5, 1, 1.5, 2}
  6. wid是上一個特徵圖的寬度，hei是上一個特徵圖的高度

把CNNBLS在MNIST和NORB資料集上測試，結果如下：

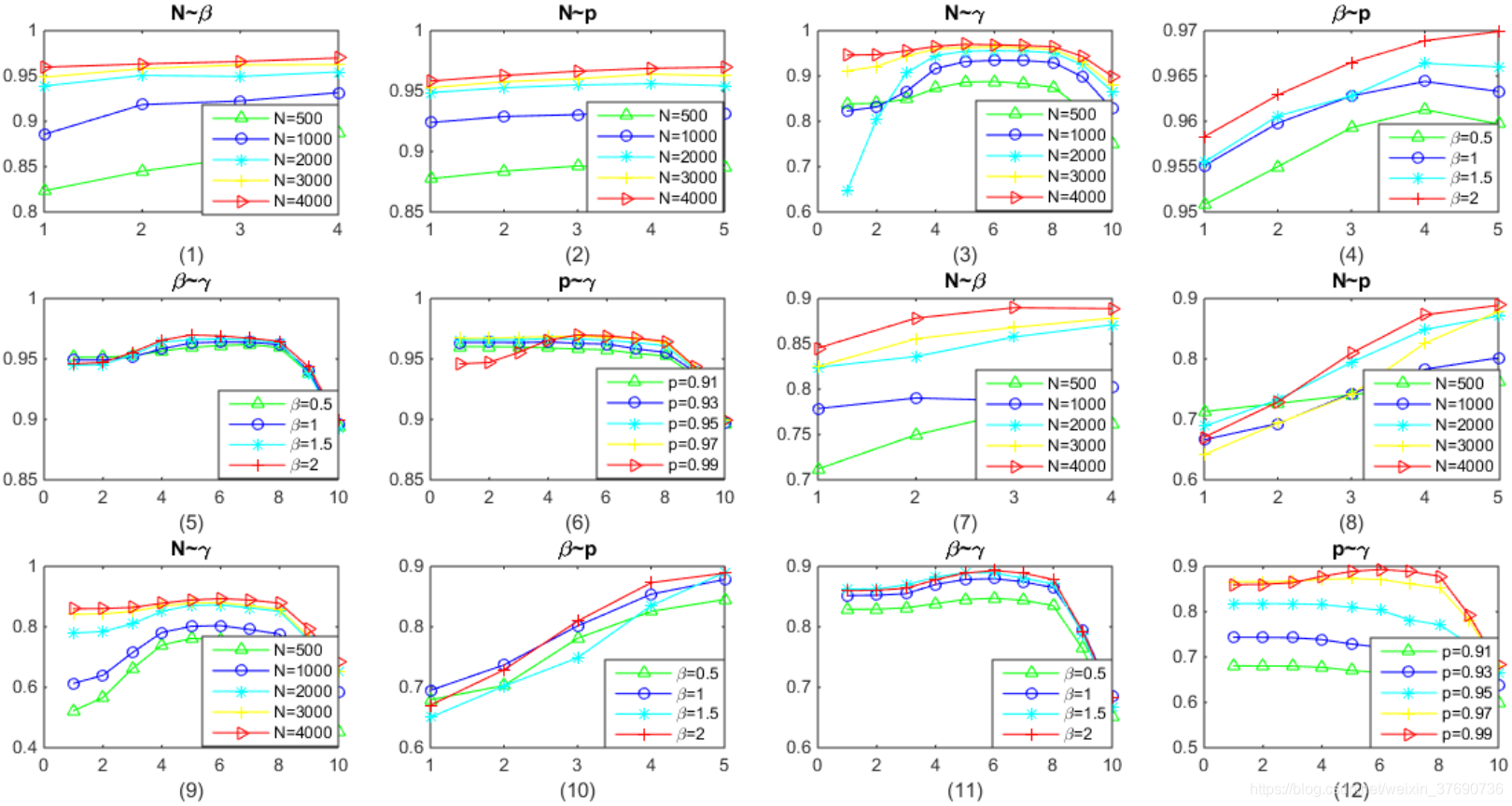
其中，圖1到圖6是MNIST資料集的結果，圖7到圖12是NORB資料集的結果。每一個圖的標題表示控制的變數，如圖1表示控制N和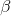\beta的值，圖例表示不同曲線顏色代表的N的值，橫座標代表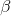\beta的取值範圍的Index。所有圖的縱座標均表示Accuarcy。

測試結論如下：

  1. Accuarcy會隨著N增大而提高
  2. Accuarcy會隨著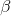\beta增大而提高
  3. Accuarcy會隨著折積核心數量增大而提高
  4. 多數情況下，Accuarcy會隨著p增大而提高
  5. Accuarcy會隨著\gamma增大先提高後下降

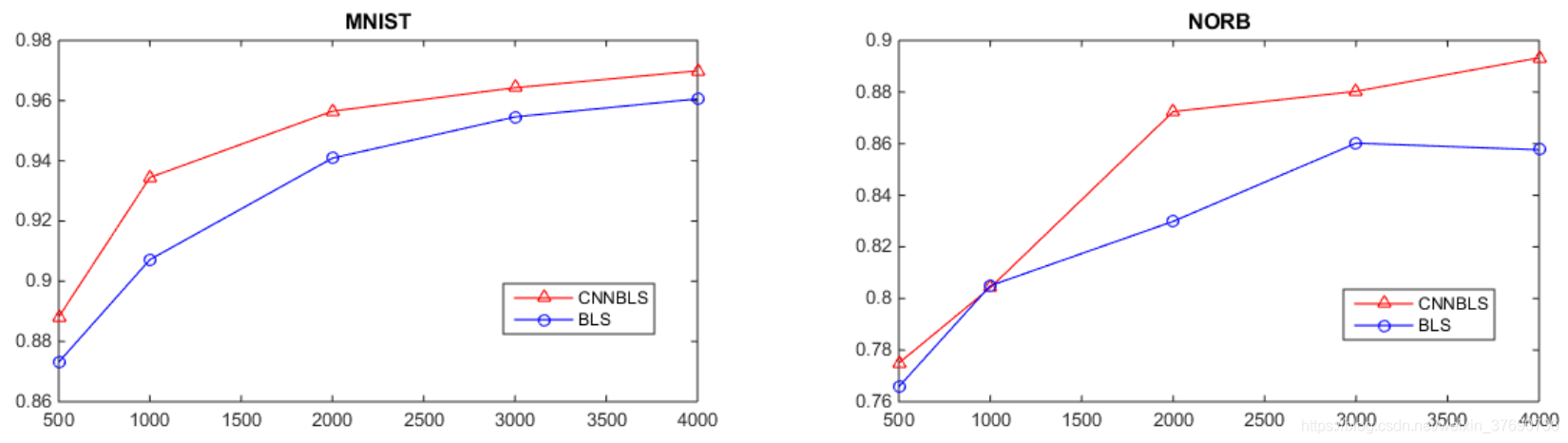
另外，作者把CNNBLS和BLS在兩個資料集上作對比，隨著測試樣本增加，CNNBLS的效能也表現的比BLS好。

總結一下，

  1. CNNBLS在計算機視覺上比BLS的效果要更好，因為CNNBLS採用折積層和池化層有效的提取資料特徵，同時減少了引數的數量。
  2. CNNBLS把所有的輸入資料用於特徵提取，而BLS在輸入資料 x 降維處理時可能丟失細節。
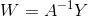  3. CNNBLS吸取了CNN和BLS的精華，能使用所有輸入資料提取特徵，類似BLS的A[ Z | H ]的過程。PCA降維後的資料應用嶺迴歸計算權重W：W=A^{-1}Y。