前言：

     你知道計算機內部是如何進行加減運算的嗎？可能你知道，那你知道計算機內部是如何進行乘除法運算的呢？肯定和我們十進位制運算是不一樣的。當我查詢資料的時候，發現除了書本很少有這樣的知識點。所以我想和大家一起分享定點數和浮點數加減乘除運算的方法，一起在二進位制的世界裡面遨遊吧~

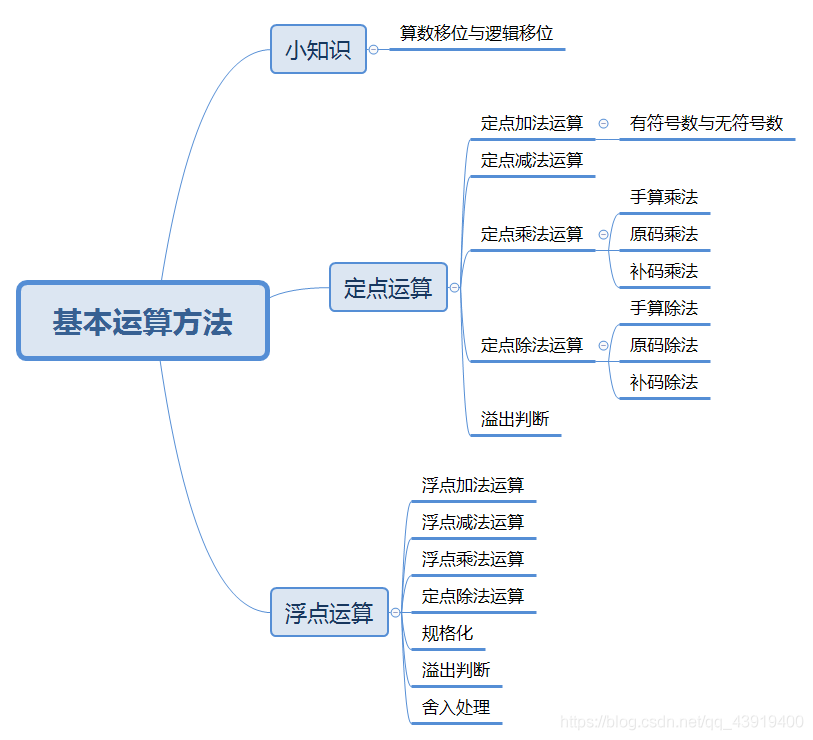
     溫馨小貼士，以下內容僅僅包含計算方法（手算和計算機內部表達部分均有），不含運算器數電知識哦。文章以下方思維導圖來展開：

---

預備知識：

     在開始之前，我們要知道定點數移位運算的知識點，在我們日常生活中總是有移位的例子。例如1500cm轉換成15m，這就是一個移位，在計算機內部，也是有移位的，但是計算機的位數是不變的，所以我們在進行移位元運算的時候就要將空缺高位或者低位的數位用0或1補齊，而我們接下來介紹的運算也和移位是分不開的，所以這裡就列出定點數的移位運算，至於為什麼沒有給出浮點數的移位運算，那是因為浮點數的移位運算是和階碼相掛鉤的（並且伴隨精度丟失），至於尾數部分和定點數的規則一致。

數的表達形式	碼制	填補程式碼	備註
正數	原碼、二補數	0	不管是左移還是右移，填0即可
負數	原碼	0	符號位不變，空位新增0即可
負數	二補數	左移添0； 右移添1

     另外有符號數的移位稱為算術移位，無符號數的移位稱為邏輯移位。邏輯移位的規則是：邏輯左移時，高位移出，低位添0；邏輯右移時，低位移出，高位添0。

---

一、定點加減法運算

（一）加法運算

1、有符號數的加法運算：

     二補數加法運算的特點就是符號位要一起作為數的一部分參與運算，其次要在模2^(n+1)的意義下相加，超過2^(n+1)的進位要丟掉，也就是說符號位的進位要丟掉。例如：

     而對於單符號位的數和雙符號位的數來說，加法法則依舊是一致的（符號位進位捨去）。它們的不同點在於：溢位判斷不一樣。

• 單符號數溢位檢測判斷一：負負得正，正正得負，那麼絕對溢位了呀！
• 單符號數溢位檢測判斷方法二：最高位和符號位有且僅由一個進位時溢位，即當最高位有進位，而符號位無進位時，產生正溢；當最高位無進位，而符號位有進位時，產生負溢。
• 雙符號位溢位判斷：兩個符號位相異時，表示溢位；相同時，表示未溢位。

     至於無符號數的加法，和上面是一致的，所有的位數都參與運算。它的溢位判斷邏輯也及其簡單。從表面上看就是如果加法變大，減法變小才符合邏輯，如果不符合這個邏輯，那肯定是不對的。那麼我們還有UOF = Sub 互斥或 Cout（這裡Sub代表減法，如果是減運算，那麼Sub = 1，如果是加運算，那麼Sub = 0。Cout代表最高位進位），所以它的判斷邏輯就是如果是加法的話，最高位有進位，那麼溢位；減法的話，最高位沒有進位，那麼溢位。

 

（二）有符號數的減法運算

     減法無非就是加上這個數的二補數的形式，即X補-Y補 = X補 + [-Y]補，其餘的運算就和加法一致了。它的溢位判斷和上面也是一致的。

---

二、定點乘除法運算

（一）乘法運算

1、手算乘法

     我覺得第一步至少要會手算乘法，所以我們一起來看看一個例子：

A = -0.1101  B = 0.1011，我們需要計算A*B的值，首先符號位單獨處理，這裡就知道是負數，數值部分就如圖所示（例子來源網上，太懶不想畫圖了，哈哈哈）：

     上面的手算我們可以觀察出，被乘數A每次進行運算之後都是要左移的，當然你也可以看成是乘數B右移，然後它們得到的數相加就得到了乘法的結果。

 

2、原碼計算

     手算小學生就會了吧，原碼的話其實也就是符號位的話單獨運算（即直接互斥或得出），數值部分就是如上的運算即可（當然你可能看到過豎式的計算，其實都是一樣的，也很好理解）。例如：我們計算X = -0.1110和Y = 0.1101的原碼乘積的時候，把符號位丟到一邊計算，互斥或就為1，為負數。然後取絕對值，即X = 0.1110，Y = 0.1101，然後開始按照第一步的手算一般運算，就得到了-0.10110110，然後把我們的符號位加上就有1.10110110，這就是最後的答案。

 

3、二補數計算

二補數一位乘運算規則：

     有被乘數X和乘數Y，那麼

• 被乘數任意，乘數為正，和原碼相乘是一致的。
• 被乘數任意，乘數為負，乘數[Y]補去掉符號位和X補運算，操作和第一個相同，最後加上[-X]補校正即可。

     這裡我們直接以例子的形式來看看，例如X = +0.0011 Y = -0.1011，求[X*Y]補（一看就是乘數為負的形式）。那麼其實也是一樣的，首先我們轉換為二補數形式，並且被乘數X以雙符號位表示，乘數Y以單符號位表示（還要計算被乘數X的負數形式的二補數）。那麼[X]補 = 00.0011，[-X]補 = 11.1101，[Y]補 = 1.0101。之後也就是：讓[X]補和[Y]補（注意，這裡是去符號位的0.0101）相乘得到00.00001111，然後加上[-X]補，就得到了結果11.11011111。

     至於溢位的判斷邏輯如下：

• 有符號數乘積的高n位全0或全1就不溢位
• 無符號數乘積的高n位全0則不溢位

 

（二）除法運算

（約定：小數定點除法，被除數絕對值小於除數；整數定點除法，被除數大於除數；除數不能為0，被除數不能為0）

1、手算除法

     對於手算除法來說，也是和我們小學所學的一致，但我們有幾個約定的規則：首先商的符號單獨計算，餘數不動低位補0減去右移一位的除數。例如X = -0.1011, Y = 0.1101。求X / Y有：

     

2、原碼除法

     原碼相除時，商的符號位由兩個符號位相加求得，商的數值位由兩數的數值部分相除得到，也就是和上面的手算除法是一至的演演算法（當然，數值部分的計算用上面的手算是可以的，也可以用下面提到的恢復餘數法和不恢復餘數法，也就是計算機內部的計算）。

     這裡用不恢復餘數法做一個例子（運算元在下面可以檢視）：

（這裡不要奇怪哦，有些地方是餘數左移然後再和除數進行計算，而我這裡是用餘數與右移的除數進行運算，其實本質都是一致的哦，我這裡將除數右移計算，這樣得到的餘數就不需要矯正了）。

 

3、二補數除法

     我們採用心算（計算機內部則是進行移位元運算）的時候總是可以判斷夠不夠減，不夠就商0，夠減商一再做處理。但是計算機內部是不能這麼做的。前輩們想到了恢復餘數法：機器先做減法，若餘數為正，才知道夠減；若餘數為負，才知道不夠減。不夠減時必須恢復到原來的餘數，以便繼續往下運算，這就是恢復餘數法。但恢復餘數使除法過程困難，不容易控制。我們就採用不恢復餘數法，也叫加減交替法。特點就是運算過程中如出現不夠減，不必恢復餘數，根據餘數符號，可以繼續往下運算。

恢復餘數法規則（若有X除以Y，Ri為餘數，Y*代表Y的絕對值）

餘數Ri>0，商1，2Ri-Y*

餘數Ri<0，商0，Ri+Y*   恢復餘數

不恢復餘數運算規則

上商1  2Ri-Y*

上商0  2Ri+Y*

     因為恢復餘數法緩慢複雜，所以大都採用不恢復餘數法。在下面例子中一起來看看二補數除法需要注意什麼呢？

有如下運算元：

    按照上面的步驟來說商符是自動形成的。接下來我們在例子中看看怎麼計算（這裡我使用單符號位，上面運算元中說採用雙符號位那是因為方便計算，但這裡單符號位即可）：

     你可能會很奇怪，為什麼我只算到了第n步，而沒有進行到n+1步計算，最後一位直接說「末位恆置1」就結束了。那是因為如果我們進行n+1次計算，到時候除不盡還需要對商值進行校正，而根據經驗我們是知道末位恆置為1，所以這裡就這樣減少了計算和檢驗步驟了。

---

三、浮點加減法運算

     浮點數加減法運算其實很簡單，總共就5步：對階、尾數運算、規格化、舍入、溢位判斷。

 1.運算步驟

    假設浮點數的階碼和尾數均用二補數表示，在浮點加減運算時，為便於浮點數尾數的規格化處理和浮點數的溢位判斷，階碼和尾數均採用雙符號位表示。

    ①對階，小階向大階對齊

    兩個浮點數進行加減運算時，首先要使兩個數的階碼相同，即小數點的位置對齊。若兩個數的階碼相同，表示小數點的位置是對齊的，就可以對尾數進行加減運算。反之，若兩個數的階碼不相同，表示小數點的位置沒有對齊，此時必須使兩個數的階碼相同，這個過程稱為對階。

    要對階，首先應求出兩個浮點數的階碼之差，即

    ΔE=[Ex]補-[Ey]補=[Ex]補+[-Ey]補

    若ΔE=0，表示兩個浮點數的階碼相等，即[Ex]補=[Ey]補；若ΔE＞0，表示 [Ex]補＞[Ey]補；若ΔE＜0，表示[Ex]補＜[Ey]補。

    當ΔE≠0時，要通過浮點數尾數的算術左移或算術右移來改變階碼，使兩個浮點數的階碼相等。理論上講，既可以通過移位[Mx]補以改變[Ex]補來達到[Ex]補=[Ey]補，也可以通過移位[My]補以改變[Ey]補來達到[Ex]補=[Ey]補。但是，由於浮點數的尾數在算術左移的過程會改變尾數的符號位，同時，尾數在算術左移的過程中還會使尾數的高位資料丟失，造成運算結果錯誤。因此，在對階時規定使小階向大階看齊，通過小階的尾數算術右移以改變階碼來達到[Ex]補=[Ey]補，尾數每右移一位，階碼加1，其數值保持不變，直到兩個浮點數的階碼相等，右移的次數等於ΔE的絕對值。

    ②尾數進行加法或減法運算

    對階結束後，即可對浮點數的尾數進行加法或減法運算。不論是加法運算還是減法運算，都按加法進行操作，其方法與定點加減運算完全一樣。

    ③結果規格化並進行舍入處理

    根據規格化浮點數的定義，當尾數用二進位制二補數表示時，規格化浮點數的尾數形式為00.1××…××或11.0××…××。若浮點數的尾數不是這兩種形式，則稱之為非規格化浮點數，需進行浮點數的規格化。

    若浮點數的尾數形式為00.0××…××或11.1××…××，應利用向左規格化使其變為規格化浮點數，尾數每算術左移1位，階碼減1，直到浮點數的尾數變成規格化形式。

    若浮點數的尾數形式為01.××…××或10.××…××，表示尾數求和的結果發生溢位，應利用向右規格化使其變為規格化浮點數，尾數算術右移1位，階碼加1，此時浮點數的尾數就變成了規格化形式。

    在對階或向右規格化時，尾數都要進行算術右移操作，為了保證運算結果的精度，運算過程中需保留右移中移出的若干位資料，稱為保護位。在運算結果進行規格化後再按照某種規則進行舍入處理以去除這些資料。舍入處理就是消除保護位資料並按照某種規則調整剩下的部分，舍入處理總要影響到資料的精度。舍入處理的方法通常選用「0舍1入」法。

    ④判斷溢位

    浮點數尾數的溢位可通過規格化進行處理，而浮點數運算結果的溢位則根據運算結果中浮點數的階碼來確定。若階碼未發生溢位，則表示運算結果未發生溢位；若階碼溢位，則需進行溢位處理。

    若階碼用雙符號位二補數表示，判斷溢位的方法為：若階碼的雙符號位相同，表示結果未發生溢位；若階碼的雙符號位不相同，表示結果發生溢位。

 

    [例1]設兩浮點數x=2001×(0.1101)，y=2011×(-0.1010)，在浮點數的表示格式中階碼佔3位，尾數佔4位元（都不包括符號位）。階碼和尾數均採用含雙符號位的二補數表示，運算結果的尾數取單字長（含符號位共5位），舍入規則用「0舍1入」法，用浮點運算方法計算x+y、x-y。

    解：[x]浮=00001，00.1101  [y]浮=00011，11.0110

    ①對階，小階向大階對齊

    ΔE=[Ex]補-[Ey]補=[Ex]補+[-Ey]補=00001+11101=11110

    x的尾數[Mx]補右移2位，階碼[Ex]補加2

    [x]浮=00011，00.0011(01)

    其中(01)表示[Mx]補右移2位後移出的最低兩位數。

    ②尾數進行加法、減法運算

 

    即[x+y]浮=00011，11.1001(01)

      [x-y]浮=00011，00.1101(01)

    ③結果規格化並進行舍入處理

    和的尾數左移1位，階碼減1，採用「0舍1入」法進行舍入處理後，得

      [x+y]浮=00010，11.0011

    差已為規格化浮點數，採用「0舍1入」法進行舍入處理後，得

      [x-y]浮=00011，00.1101

    ④判斷溢位

    和、差的階碼的雙符號位均相同，故和、差均無溢位。

    所以x+y=2010×(-0.1101)

        x-y=2011×(0.1101)

 

[例2]設兩浮點數x=2－011×(0.100101)，y=2－010×(-0.011110)，在浮點數的表示格式中階碼佔3位，尾數佔6位（都不包括符號位）。階碼和尾數均採用含雙符號位的二補數表示，運算結果的尾數取單字長（含符號位共7位），舍入規則用「0舍1入」法，用浮點運算方法計算x+y、x-y。

    解：[x]浮=11101，00.100101  [y]浮=11110，11.100010

    ①對階，小階向大階對齊

    ΔE=[Exx]補-[Ey]補=[Ex]補+[-Ey]補=11101+00010=11111

    x的尾數[Mx]補右移1位，階碼[Ex]補加1

    [x]浮=11110，00.010010(1)

    其中(1)表示[Mx]補右移1位後移出的最低一位數。

    ②尾數進行加法、減法運算

 

    即[x+y]浮=11110，11.110100(1)

      [x-y]浮=11110，00.110000(1)

    ③結果規格化並進行舍入處理

    和的尾數左移2位，階碼減2，得

    [x+y]浮=11100，11.010010

    差已為規格化浮點數，採用「0舍1入」法進行舍入處理後，得

    [x-y]浮=11110，00.110001

    ④判斷溢位

    和、差階碼的雙符號位均相同，故和、差均無溢位。

    所以x+y=2-100×(-0.101110)

        x-y=2-010×(0.110001)

---

四、浮點乘除法運算

     浮點乘除法其實很簡單，浮點數乘法：階碼相加、尾數相乘、結果規格化；浮點數除法：尾數調整、階碼求差、尾數相除

    1.運算步驟

    在浮點乘除運算時，為便於浮點數判斷溢位和尾數進行陣列乘除運算運算，假設浮點數的階碼採用雙符號位二補數表示，尾數採用單符號二補數或原碼錶示。

    浮點乘法、除法運算步驟如下：

    ①階碼相加減

    按照定點整數的加減法運算方法對兩個浮點數的階碼進行加減運算。

    ②尾數相乘或相除

    按照定點小數的陣列乘除法運算方法對兩個浮點數的尾數進行乘除運算。為了保證尾數相除時商的正確性，必須保證被除數尾數的絕對值一定小於除數尾數的絕對值。若被除數尾數的絕對值大於除數尾數的絕對值，需對被除數進行調整，即被除數的尾數每右移1位，階碼加1，直到被除數尾數的絕對值小於除數尾數的絕對值。

    ③結果規格化並進行舍入處理

    浮點數乘除運算結果的規格化和舍入處理與浮點數加減運算結果的規格化和舍入處理方法相同。並且在浮點數乘除運算的結果中，由於乘積和商的絕對值一定小於1，因此在浮點乘除運算結果進行規格化處理時只存在向左規格化，不可能出現向右規格化。

    ④判斷溢位

    浮點數乘除運算結果的尾數不可能發生溢位，而浮點數運算結果的溢位則根據運算結果中浮點數的階碼來確定，溢位的判定和處理方法與浮點加減運算完全相同。

 

    [例1]設兩浮點數x=2－001×(-0.100010)，y=2－100×(0.010110)，在浮點數的表示格式中階碼佔3位，尾數佔6位（都不包括符號位），階碼採用雙符號位的二補數表示，尾數用單符號位的二補數表示。要求用直接二補數陣列乘法完成尾數乘法運算，運算結果的尾數取單字長（含符號位共7位），舍入規則用「0舍1入」法，用浮點運算方法計算x×y。

    解：[x]浮=11111，1.011110  [y]浮=11100，0.010110

    ①階碼相加

    [Ex+Ey]補=[Ex]補+[Ey]補=11111+11100=11011

    ②尾數作直接二補數陣列乘法運算

 

    [Mx]補×[My]補=1.110100010100

    ③結果規格化並進行舍入處理

    積的尾數左移2位，階碼減2，採用「0舍1入」法進行舍入處理後，得

    [x×y]浮=11001，1.010001

    ④判斷溢位

    乘積的階碼的雙符號位相同，故乘積無溢位。

    所以x×y=2－111×(-0.101111)

 

    [例2]設兩浮點數x=2－010×(0.011010)，y=2011×(-0.111100)，在浮點數的表示格式中階碼佔3位，尾數佔6位（都不包括符號位），階碼採用雙符號位的二補數表示，尾數用單符號位的原碼錶示。要求用原碼陣列除法完成尾數除法運算，運算結果的尾數取單字長（含符號位共7位），舍入規則用「0舍1入」法，用浮點運算方法計算x÷y。

    解：[x]浮=11110，0.011010  [y]浮=00011，1.111100

    ①階碼相減

    [Exx-Ey]補=[Ex]補+[-Ey]補=11110+11101=11011

    ②尾數作原碼陣列除法運算

    [Mx]原=0.011010  [My]原=1.111100

    商的符號位為：Mxf⊕Myf=0⊕1=1

    令Mx’=011010000000，My’=111100，其中Mx’和My’分別為[Mx]原和[My]原的數值部分，且Mx’為雙字長

    [Mx’]補=0011010000000，[My’]補=0111100，[-My’]補=1000100

 

    故得商q=0011011

    所以[Mx÷My]原=1.011011

    因此[x÷y]浮=11011，1.011011

    ③尾數規格化

    商的尾數左移1位，階碼減1。

    [x÷y]浮=11010，1.110110

    ④判斷溢位

    商的階碼的雙符號位相同，故商無溢位。

    所以x÷y=2-110×(-0.110110)

---

後記：

     額，寫到這裡我快沒了，哈哈哈。其實掌握了定點數部分，到浮點數部分只要按照具體的步驟來，就水到渠成。而且你也會發現，加減法簡單，乘法還好，除法就特別難了，計算機內部還要進行很多判斷和移位元運算，所以各位寫程式碼的，儘量少用除法呀！！！

 

參考資料：

https://blog.csdn.net/xingqingly/article/details/18981671?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param，後半部分浮點數運算均來源於此，特做說明，因為寫的很好了，就不需要自己再去寫了，謝謝大佬的資料。