讀書筆記-增量學習-Broad Learning System: An Effective and Efficient Incremental Learning System
一篇2018年澳門大學科技學院前院長陳俊龍先生的論文: Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture。作者在題目已表明這是一種顛覆以往縱向神經網路架構的有效且高效的增量學習系統。傳統的神經網路通常因為在 filters 和 layers 間有大量引數存在,導致模型訓練與擴充套件階段十分耗時。因此作者提出Broad Learning System(BLS)寬度學習系統,一種基於Random Vector Functional-link neural networks(RVFLNN)隨機向量函數連結神經網路的增量學習模型。
-
什麼是RVFLNN?
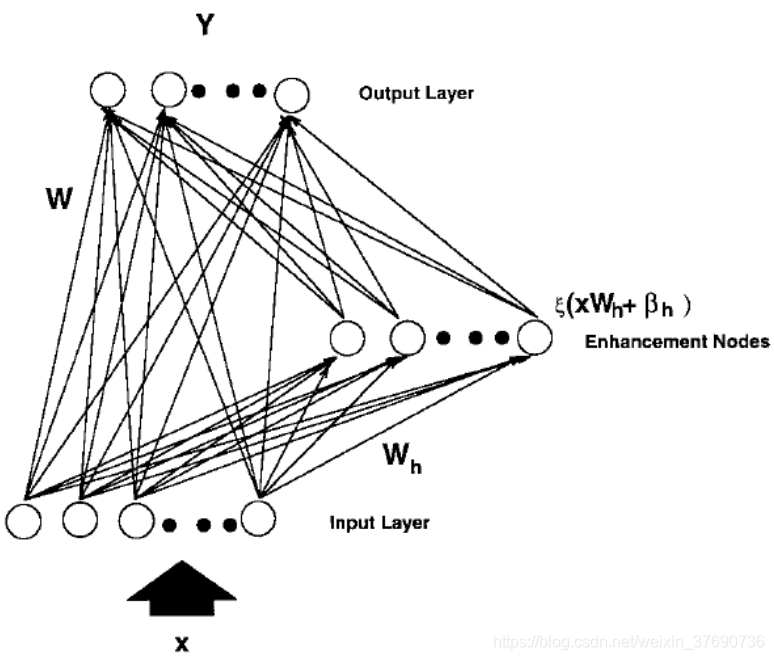
上圖是對RVFLNN的圖解,x 作為Input data被輸入到Input Layer, 與常規做法不同,RVFLNN把輸入 x 乘上一組隨機權重 W 再加一個隨機bias,這部分資料經由啟用函數處理後,由Enhancement nodes中輸出,記作 H。隨後把 x 和 H 合併成一個矩陣 A,記作 A = [ x | H ]。此時把A作為輸入,乘上另一組權重再加一個bias,傳入Output Layer得到最終結果 Y。注意,x乘上的隨機權重W在選定後就不再改變。
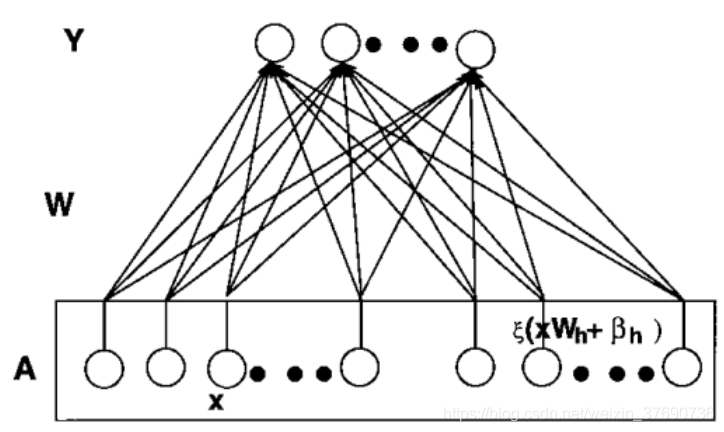
上圖做了一個變形,把Input data 和 Enhancement Nodes 看作一個整體 A,我們知道,AW = Y。由於Input data變換為Enhancement nodes過程中的權重不再改變,整個神經網路的訓練其實可以看作由 A 和 Y 求 W 的過程。
由於Input data x 已知,輸入層到增強層的權重已知,即 A 也可以求得。由Input data x的標籤數量知道輸出 Y 的規模。因此,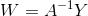 可解。
可解。
簡而言之,RVFLNN就是將原始輸入資料 x1 做一個對映後,作為另一組輸入 x2,把 x1 和 x2 一起作為輸入訓練得到輸出 Y。
-
什麼是BLS?
Broad Learning System(BLS)基於RVFLNN做了改進,並支援Incremental Learning增量學習。
-
不含增量學習的BLS

上圖是不含增量學習的BLS結構圖,其中,Mapped Feature、Mapped Node、Enhancement Node的數量都是人為規定好。共分為3個步驟:
- 與RVFLNN不同,輸入資料 X 先進行處理(特徵提取),把輸入資料對映為多個Mapped nodes, 這些nodes可以分類成為 Mapped Feature。圖中Z1 .. Zn即為這部分資料,類似與RVFLNN中的輸入資料 x。
- 把 Z1 .. Zn 乘上一組隨機權重W再加上bias,啟用函數處理後作為Enhancement nodes的輸出,記作H1 .. Hm。這部分與RVFLNN中增強層一致。
- 最後把 Z1 .. Zn 與 H1 .. Hm 合併,記作 A = [ Z | H ],輸出
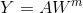 。
。
-
包含增量學習的BLS
在上述BLS架構下實現增量學習,即有3個方向可延伸:
- Increment of the enhancement nodes(Enhancement node的增加)
- Increment of the feature nodes(Feature node的增加)
- A new coming input(輸入資料的增加)
論文對3個擴充套件方向均提出了對應演演算法,接下來一一介紹。
-
Increment of the enhancement nodes(Enhancement node的增加)

當BLS的效能下降,其中一個方法就是引入一個新的Enhancement node記作 P 以降低Loss。
原來的A記作![A^{m}=[Z^{n} | H^{m}]](https://s3.ap-northeast-1.wasabisys.com/img.tw511.com/202010/gifbshbw5u5zbh.gif) ,引入新節點後,記作
,引入新節點後,記作![]() 。其中
。其中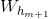 和
和 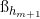
均隨機生成,矩陣合併後得到 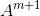 ,從而求得新的權重。增加Enhancement node的虛擬碼如下:
,從而求得新的權重。增加Enhancement node的虛擬碼如下:

- Increment of the Feature nodes(Feature node的增加)

上圖增加了Mapped Feature的顯示,與增加Enhancement node不同。先隨機生成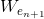 和
和 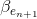 ,用輸入資料 X 乘以
,用輸入資料 X 乘以 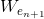 再加上
再加上 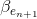 得到
得到 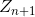 。然後隨機生成
。然後隨機生成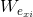 和
和 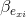 (i = 1 ... m),求得
(i = 1 ... m),求得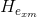 。從而得到新的
。從而得到新的 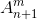 (表示n+1組mapped features & m組enhancement nodes)。增加Feature node的虛擬碼如下:
(表示n+1組mapped features & m組enhancement nodes)。增加Feature node的虛擬碼如下:

- A new coming input(輸入資料的增加)
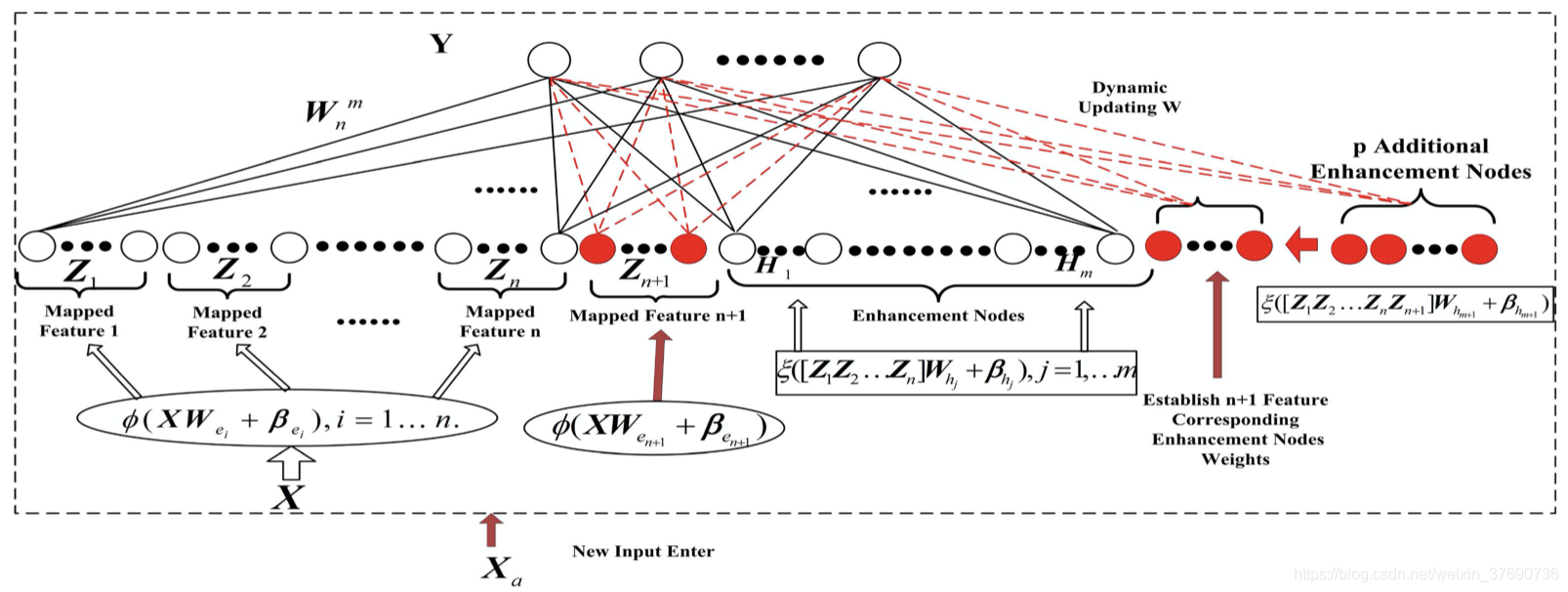
虛擬碼如下:

其中,以上提及的由 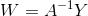 的求解方式在論文中也有介紹,詳細方法如下:
的求解方式在論文中也有介紹,詳細方法如下:
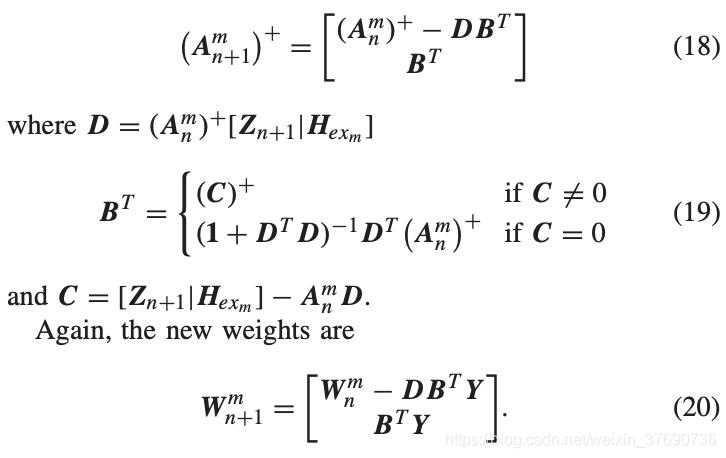
可見,求解新的權重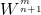 會重用上一次的權重
會重用上一次的權重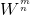 ,因而有效減少更新權重的計算量。
,因而有效減少更新權重的計算量。
最後,BLS最重要的特點在於單隱層結構,具有「橫向擴充套件」和「增量學習」兩大優勢。當模型效能下降時,以往的神經網路採用增加Layer或調參,BLS可採用橫向擴充套件的方式,增加新的增強節點、特徵節點、輸入資料。不需要從頭學習,也不會導致災難性遺忘。因而論文的確如題目所說的 Effient 和 Effective。