在圖上傳送訊息的神經網路MPNN簡介和程式碼實現

歡迎來到圖神經網路的世界，在這裡我們在圖上構建深度學習模型。你可以認為這很簡單。畢竟，我們難道不能重用使用正常資料的模型嗎?

其實不是。在圖中所有的資料點(節點)是相互連線的。這意味著資料不再是獨立的，這使得大多數標準的機器學習模型毫無用處，因為它們的推導都強烈地基於這個假設。為了克服這個問題，可以從圖中提取數位資料，或者使用直接對這類資料進行操作的模型。

建立直接在圖上工作的模型更為理想，因為我們可以獲得更多關於圖的結構和屬性的資訊。在本文中，我們將研究一種專門為此類資料設計的架構，即訊息傳遞神經網路(MPNNs)。

模型的各種變體

在將模型標準化為單個MPNN框架之前，幾位獨立研究人員已經發布了不同的變體。這種型別的結構在化學中特別流行，可以幫助預測分子的性質。

Duvenaud等人在2015年發表了有關該主題的第一批著作之一[1]。他使用訊息傳遞體系結構從圖分子中提取有價值的資訊，然後將其轉換為單個特徵向量。當時，他的工作具有開創性，因為他使體系結構與眾不同。實際上是最早可以在圖上執行的折積神經網路體系結構之一。

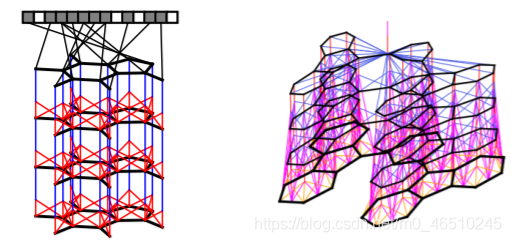
Duvenaud等人建立的訊息傳遞體系結構。他將模型定義為可區分的層的堆疊，其中每一層是傳遞訊息的另一輪。修改自[1]

Li等人在2016年對此構架進行了另一嘗試[2]。在這裡，他們專注於圖的順序輸出，例如在圖[2]中找到最佳路徑。為此，他們將GRU（門控迴圈單元）嵌入其演演算法中。

儘管這些演演算法似乎完全不同，但是它們具有相同的基本概念，即訊息在圖中的節點之間傳遞。我們將很快看到如何將這些模型組合成一個框架。

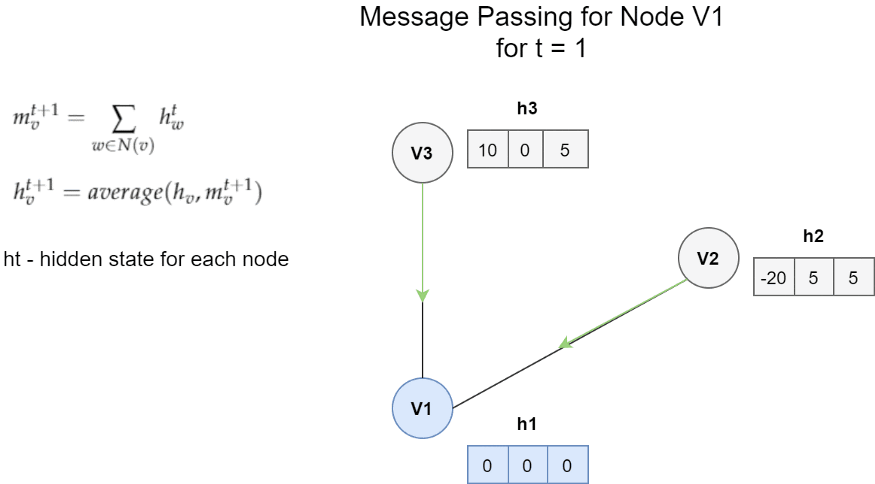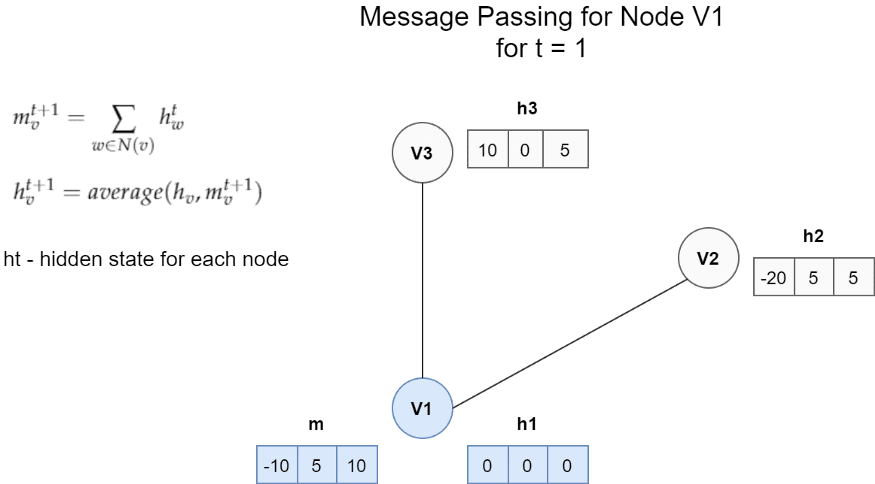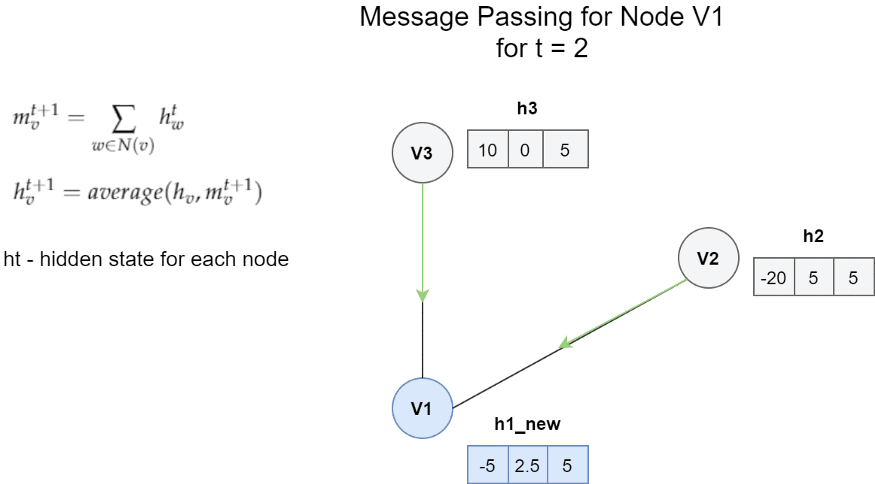
節點V1的訊息傳遞體系結構的一個非常簡單的範例。在這種情況下，一條訊息是鄰居的隱藏狀態的總和。更新函數是訊息m和h1之間的平均值。

畢竟，MPNN背後的想法在概念上很簡單。

圖中的每個節點都具有隱藏狀態（即特徵向量）。對於每個節點Vt，我們將隱藏狀態的函數以及所有相鄰節點的邊緣與節點Vt本身進行聚合。然後，我們使用獲得的訊息和該節點的先前隱藏狀態來更新節點Vt的隱藏狀態。

有3個主要方程式定義圖[3]上的MPNN框架。從相鄰節點獲得的訊息由以下公式給出：

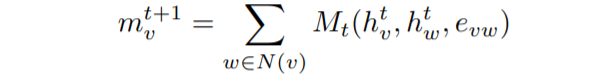
從鄰居節點獲取訊息。

它是從鄰居獲得的所有訊息Mt的總和。 Mt是取決於隱藏狀態和相鄰節點邊緣的任意函數。我們可以通過保留一些輸入引數來簡化此功能。在上面的範例中，我們僅求和不同的隱藏狀態hw。

然後，我們使用一個簡單的方程式更新節點Vt的隱藏狀態：

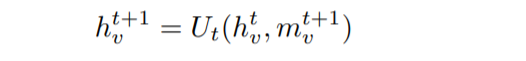
使用先前的隱藏狀態和新訊息更新節點的狀態。

簡單地說，通過用新獲得的訊息mv更新舊的隱藏狀態來獲得節點Vt的隱藏狀態。在上述範例的情況下，更新函數Ut是先前隱藏狀態和訊息之間的平均值。

我們將此訊息傳遞演演算法重複指定的次數。之後，我們進入最後的讀出階段。

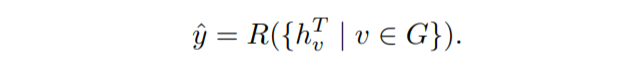
將獲得的隱藏狀態對映到描述整個圖形的單個特徵向量中。

在此步驟中，我們提取所有新近更新的隱藏狀態，並建立描述整個圖形的最終特徵向量。然後可以將此特徵向量用作標準機器學習模型的輸入。

就是這樣！這些是MPNN的基礎。這個框架非常強大，因為我們可以定義不同的訊息並根據想要實現的功能更新功能。我建議檢視[3]以獲得更多資訊，以瞭解MPNN模型的不同變體。

MPNN已經被少數深度學習庫實現。以下是一些我可以找到的不同實現的列表：

原始模型程式碼 https://github.com/brain-research/mpnn

Deepchem整合https://github.com/deepchem/deepchem/tree/master/contrib/mpnn

PyTorch的Geometric實現 https://github.com/rusty1s/pytorch_geometric

MPNN框架標準化了由多個研究人員獨立建立的不同訊息傳遞模型。該框架的主要思想包括訊息，更新和讀出功能，它們在圖中的不同節點上執行。 MPNN模型的一些變體共用此功能，但是它們的定義不同。

[1] Convolutional Networks on Graphs for Learning Molecular Fingerprints

[2] Gated Graph Sequence Neural Networks

[3] Neural Message Passing for Quantum Chemistry

作者：Kacper Kubara

deephub翻譯組