1577：【例 3】數位轉換(求樹的直徑——兩遍dfs找樹的直徑的端的/樹形DP求解)

1577：【例 3】數位轉換
問題描述
如果一個數 x 的約數和 y （不包括他本身）比他本身小，那麼 x 可以變成 y，y 也可以變成 x。例如 4 可以變為 3，1 可以變為 7。限定所有數位變換在不超過 n 的正整數範圍內進行，求不斷進行數位變換且不出現重複數位的最多變換步數。

思路

1. 題意：x 所有約數的和為 y，那麼 x 就可以和 y 互相轉化（在 x<y 的前提下），首先我們預處理 1~n 中的每個數位 x，可以轉化為那個數 y，我們在 x 與 y 之間建立一條邊，這樣預處理完之後，形成以 1 為根節點的一顆樹，
2. 題目就是讓求這個樹中的直徑是多少？

樹的直徑

• 樹的直徑定義：在一棵樹中的任意兩個節點之間（這兩個節點都應該是：葉子結點）的簡單路徑的最長距離（樹的直徑不唯一）。

解法一：找樹的直徑的兩個端點

1. 以樹中的任意一個節點 x，進行深搜，找到距離 x 最遠的那個葉子節點 s，s 就是樹的直徑的其中的一個端點，
2. 再以 s 進行深搜，找到距離 s 最遠的葉子節點 e，e 是樹的直徑的另一個端點，在此次深搜的時候我們已經得到的 s->e 樹的直徑距離了，

• 證明傳送門

程式碼

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <queue>
#include <map>
/* #include <unordered_map> */
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define db double
#define Pir pair<int, int>
#define m_p make_pair
#define INF 0x3f3f3f3f
#define esp 1e-7
#define for_(i, s, e) for(int i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(int i = (ll)(e); i >= (ll)(s); i --)
#define sc scanf
#define pr printf
#define sd(a) scanf("%d", &a)
#define ss(a) scanf("%s", a)
#define size() size() * 1LL
#define mod (ll)(10007)
#define Min(a, b, c) min(a, min(b, c))
#define Max(a, b, c) max(a, max(b, c))
using namespace std;

const int mxn = 50005;
vector<int> e[mxn];

int sov(int x)
{
    int sum = 0;
    for(int i = 1; i * i <= x; i ++)
    {
        if(x % i) continue;
        sum += i;
        if(x / i != i && i != 1)
            sum += x / i;
    }
    return sum;
}
Pir a, b;
int dep[mxn];
void dfs(int u, int p, int dep[], Pir & c)
{
    dep[u] = dep[p] + 1;
    if(c.se < dep[u])
    {
        c.se = dep[u];
        c.fi = u;
    }

    for_(i, 0, e[u].size() - 1)
    {
        int v = e[u][i];
        if(v == p) continue;
        dfs(v, u, dep, c);
    }
}

int main()
{
    /* fre(); */
    int n; sd(n);

    for_(i, 2, n)
    {
        int sm = sov(i);
        if(sm < i)
        {
            e[i].pb(sm);
            e[sm].pb(i);
        }
    }

    dfs(1, 0, dep, a);
    memset(dep, 0, sizeof(dep));
    dfs(a.fi, 0, dep, b);
    pr("%d\n", b.se - 1);

    return  0;
}

解法二——樹形DP

1. 對於這種解法，我只需要弄懂它的狀態轉移方程，就好說了，

2. 定義：dp [mxn][3],

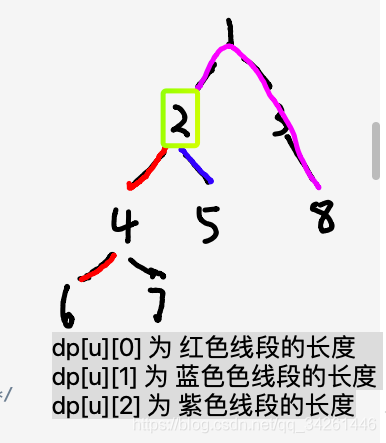
   1. dp [u][0] 表示以 u 為根的子樹中，u 到其葉子所有節點中最遠距離是多少，
   2. dp [u][1] 表示以 u 為根的子樹中，u 到其葉子所有節點中次遠距離是多少，
   3. dp [u][2] 表示 整棵樹 G 挖去 子樹部分之後，剩餘部分的樹$G^{\prime }$ 中的葉子節點的到 u 的最大距離，舉例如下圖表示 (當u ==2時)
      

3. 在上面這個圖中，子節點 2 能產生最大距離（產生樹的直徑距離）的話，產生的方式有兩種：

   1. 紅色部分的長度 + 紫色部分的長度
   2. 紅色部分的長度 + 藍色部分的長度

4. 在這兩個方案中的 去最大值就可可以得到經過 2 節點路徑的最大長度，如果我們樹中所有的節點所能產生的最大值去最優值，那麼這個最優值就是樹的直徑了，

5. 對於求解 樹中每一個節點 u 的 dp [u][0]、dp [u][1] 的話 我們用一個 dfs 就可以直接求出來了，

6. 但是對於 dp [u][2] 的求法思路是：我在另一個 dfs 函數中，在從上往下遞迴的時候我們利用 當前遞迴的到的節點 u 的 dp [u][0~2] 之間的資料來更新的它的所有子節點的 dp [v][2] 的值，例如在這個圖中如果我們 dfs 到了節點 2，現在要更新它的子節點 4 的 dp [4][2] 的值，

   1. 因為節點 2 的 dp [2][0] (紅色那部分) 經過了要更新的節點 4， dp [4][2] 的的值 = max（藍色線段長度（dp [2][1]） ，紫色線段長度 (dp [2][2])）+ （2-4 這條邊之間的長度），
   2. 如果節點 2 的 dp [2][0] (紅色那部分) 沒有經過了要更新的節點 4，那麼 dp [4][2] 的的值 = max（紅色線段長度（dp [2][0]） ，紫色線段長度 (dp [2][2])）+ （2-4 這條邊之間的長度），

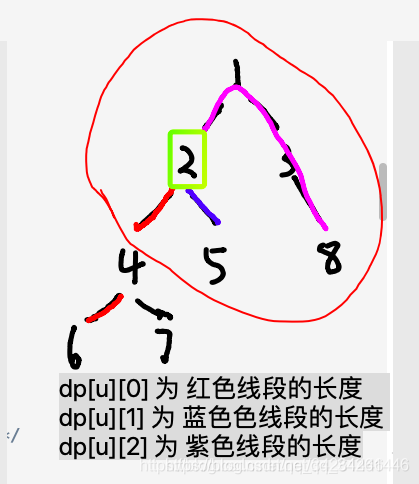
這種解法的思路就是這樣，具體實現看程式碼。。。。。。。。。。。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <queue>
#include <map>
/* #include <unordered_map> */
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define db double
#define Pir pair<int, int>
#define m_p make_pair
#define INF 0x3f3f3f3f
#define esp 1e-7
#define for_(i, s, e) for(int i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(int i = (ll)(e); i >= (ll)(s); i --)
#define sc scanf
#define pr printf
#define sd(a) scanf("%d", &a)
#define ss(a) scanf("%s", a)
#define size() size() * 1LL
#define mod (ll)(10007)
#define Min(a, b, c) min(a, min(b, c))
#define Max(a, b, c) max(a, max(b, c))
using namespace std;

const int mxn = 50005;
vector<int> e[mxn];

int sov(int x)
{
    int sum = 0;
    for(int i = 1; i * i <= x; i ++)
    {
        if(x % i) continue;
        sum += i;
        if(x / i != i && i != 1)
            sum += x / i;
    }
    return sum;
}

int dis[mxn][3];
int mxson[mxn];

void dfs(int u, int p)
{
    for_(i, 0, e[u].size() - 1)
    {
        int v = e[u][i];
        if(v == p) continue;
        dfs(v, u);

        int d = dis[v][0] + 1;
        if(d >= dis[u][0])
        {
            dis[u][1] = dis[u][0];
            dis[u][0] = d;
            mxson[u] = v;
        }
        else if(d > dis[u][1])
            dis[u][1] = d;
    }
}

void dfs2(int u, int p)
{
    for_(i, 0, e[u].size() - 1)
    {
        int v = e[u][i];
        if(v == p) continue;

        if(mxson[u] != v)
            dis[v][2] = max(dis[u][0], dis[u][2]) + 1;
        else
            dis[v][2] = max(dis[u][1], dis[u][2]) + 1;
        dfs2(v, u);
    }
}


int main()
{
    /* fre(); */
    int n; sd(n);

    for_(i, 2, n)
    {
        int sm = sov(i);
        if(sm < i)
        {
            e[i].pb(sm);
            e[sm].pb(i);
        }
    }

    dfs(1, 0);
    dfs2(1, 0);

    int mx = 0;
    for_(i, 1, n)
    {
        mx = Max(mx, dis[i][0], dis[i][2]);
    }
    pr("%d\n", max(mx, 0));

    return  0;
}