圖論-單源最短路徑(Dijskal演演算法)
文章目錄
Dijkstra
Dijkstra演演算法是圖論中用來求單源最短路徑的經典演演算法,複雜度可以優化到
O
(
m
l
o
g
(
n
)
)
O(mlog(n))
O(mlog(n))。從整體上看就是從一個起點,擴散到整個圖的過程。
打個比方,把圖的邊看成多米諾骨牌,骨牌數量和邊的權值成正比,假設骨牌倒下速度一樣,從起點推倒骨牌,所連邊上的骨牌都倒下,到達所有能到達的終點。並且某個結點先倒下來的骨牌就是最短路徑,後倒過來的骨牌對最短路徑沒有貢獻,忽略之。
原理
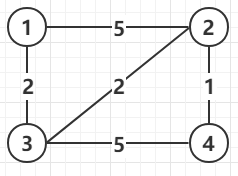
Dijkstra演演算法應用了貪心的思想,即「抄近路走」。維護兩個集合
A
A
A和
B
B
B,
A
A
A表示已確定最短路徑的結點集(紅色表示),
B
B
B表示鄰居結點(藍色表示)。
-
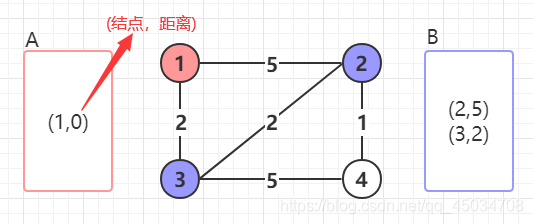
首先把起點1放入 A A A中,把它的所有鄰居放入 B B B中
-
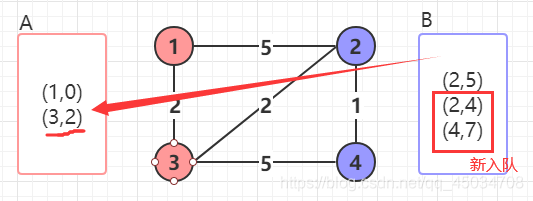
在 B B B中找距離起點最短的結點放入 A A A中,即結點3,並把它的鄰居加入進 B B B,距離是起點到該節點的距離+該節點到鄰居的距離。
-
此時 B B B中存在相同結點2,我們取距離更短的那個,即捨棄(2,5)
-
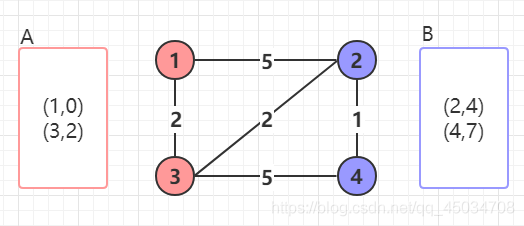
以此類推,把 B B B中距離最短的結點2放入 A A A中,加入鄰居,然後捨棄更遠的(4,7)
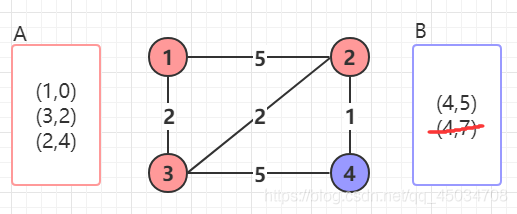
-
最後得到起點到其他結點的最短路徑
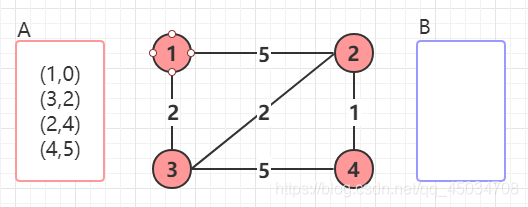
上述方法中,對於每次尋找 B B B中距離最近結點,可以用優先佇列實現,這樣依賴複雜度就能優化到 O ( m l o g ( n ) ) O(mlog(n)) O(mlog(n))。
如果要列印路徑,定義一個陣列 p r e [ ] pre[] pre[]記錄前驅結點就好了,也就是它是作為誰的鄰居進入 B B B中的,然後遞迴列印。
模板
struct edge { //邊
int from, to, w; //起點,終點,權值
edge(int a, int b, int c) {
from = a, to = b, w = c;
}
};
struct node {
int id, dis; //即圖解中的(結點,距離)
node(int a, int b) {
id = a, dis = b;
}
bool operator< (const node &a)const {
return a.dis < dis;
}
};
int n, m, x, y, z;
vector<edge>e[maxn]; //鄰接表存圖
int dis[maxn], pre[maxn]; //記錄最短路徑和 前驅節點
bool vis[maxn]; //記錄是否已入A,實現捨棄操作
void print_path(int s, int t) { //列印起點s到點t最短路徑
if (s == t)return;
print_path(s, pre[t]);
printf("%d ", t);
}
void dijkstra(int s) { //傳入起點
memset(dis, inf, sizeof(dis));
memset(vis, false, sizeof(vis));
dis[s] = 0;
priority_queue<node>q; //優先佇列
q.push(node(s, dis[s])); //入隊起點
while (!q.empty()) {
node cur = q.top();
q.pop();
if (vis[cur.id])continue;
vis[cur.id] = true; //即已找到最短路徑
for (int i = 0; i < e[cur.id].size(); i++) { //檢查所有鄰居
edge nex = e[cur.id][i];
if (vis[nex.to])continue; //捨棄(更優的已經get)
if (dis[nex.to] > nex.w + cur.dis) { //擴充套件新鄰居
dis[nex.to] = nex.w + cur.dis;
q.push(node(nex.to, dis[nex.to]));
//pre[nex.to] = cur.id; //記錄路徑
}
}
}
}
例題
HDU-2544 最短路
Problem Description
在每年的校賽裡,所有進入決賽的同學都會獲得一件很漂亮的t-shirt。但是每當我們的工作人員把上百件的衣服從商店運回到賽場的時候,卻是非常累的!所以現在他們想要尋找最短的從商店到賽場的路線,你可以幫助他們嗎?
Input
輸入包括多組資料。每組資料第一行是兩個整數N、M(N<=100,M<=10000),N表示成都的大街上有幾個路口,標號為1的路口是商店所在地,標號為N的路口是賽場所在地,M則表示在成都有幾條路。N=M=0表示輸入結束。接下來M行,每行包括3個整數A,B,C(1<=A,B<=N,1<=C<=1000),表示在路口A與路口B之間有一條路,我們的工作人員需要C分鐘的時間走過這條路。
輸入保證至少存在1條商店到賽場的路線。
Output
對於每組輸入,輸出一行,表示工作人員從商店走到賽場的最短時間
Sample Input
2 1
1 2 3
3 3
1 2 5
2 3 5
3 1 2
0 0
Sample Output
3
2
分析:模板題
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn = 102;
struct edge {
int from, to, w;
edge(int a, int b, int c) {
from = a, to = b, w = c;
}
};
struct node {
int id, dis;
node(int a, int b) {
id = a, dis = b;
}
bool operator< (const node &a)const {
return a.dis < dis;
}
};
int n, m, x, y, z;
vector<edge>e[maxn];
int dis[maxn];
bool vis[maxn];
void dijkstra(int s) {
dis[s] = 0;
priority_queue<node>q;
q.push(node(s, dis[s]));
while (!q.empty()) {
node cur = q.top();
q.pop();
if (vis[cur.id])continue;
vis[cur.id] = true;
for (int i = 0; i < e[cur.id].size(); i++) {
edge nex = e[cur.id][i];
if (vis[nex.to])continue;
if (dis[nex.to] > nex.w + cur.dis) {
dis[nex.to] = nex.w + cur.dis;
q.push(node(nex.to, dis[nex.to]));
}
}
}
}
int main() {
while (~scanf("%d%d", &n, &m)) {
if (n == 0 && m == 0)break;
for (int i = 1; i <= n; i++)e[i].clear();
memset(dis, inf, sizeof(dis));
memset(vis, false, sizeof(vis));
while (m--) {
scanf("%d%d%d", &x, &y, &z);
e[x].push_back(edge(x, y, z));
e[y].push_back(edge(y, x, z));
}
dijkstra(1);
printf("%d\n", dis[n]);
}
return 0;
}
HDU-2680 Choose the best route
HDU-2680 Choose the best route
Problem Description
One day , Kiki wants to visit one of her friends. As she is liable to carsickness , she wants to arrive at her friend’s home as soon as possible . Now give you a map of the city’s traffic route, and the stations which are near Kiki’s home so that she can take. You may suppose Kiki can change the bus at any station. Please find out the least time Kiki needs to spend. To make it easy, if the city have n bus stations ,the stations will been expressed as an integer 1,2,3…n.
Input
There are several test cases.
Each case begins with three integers n, m and s,(n<1000,m<20000,1=<s<=n) n stands for the number of bus stations in this city and m stands for the number of directed ways between bus stations .(Maybe there are several ways between two bus stations .) s stands for the bus station that near Kiki’s friend’s home.
Then follow m lines ,each line contains three integers p , q , t (0<t<=1000). means from station p to station q there is a way and it will costs t minutes .
Then a line with an integer w(0<w<n), means the number of stations Kiki can take at the beginning. Then follows w integers stands for these stations.
Output
The output contains one line for each data set : the least time Kiki needs to spend ,if it’s impossible to find such a route ,just output 「-1」.
Sample Input
5 8 5
1 2 2
1 5 3
1 3 4
2 4 7
2 5 6
2 3 5
3 5 1
4 5 1
2
2 3
4 3 4
1 2 3
1 3 4
2 3 2
1
1
Sample Output
1
-1
分析:
站臺編號1~n,假設起點是0(超級源點),那麼可以直接出發的點置距離為0,然後套演演算法即可。
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn = 1003;
struct node {
int id, dis;
node(int a, int b) {
id = a, dis = b;
}
bool operator <(const node& a)const {
return a.dis < dis;
}
};
int mp[maxn][maxn], dis[maxn];
bool vis[maxn];
int n, m, e, x, y, z;
void dijkstra() {
dis[0] = 0;
priority_queue<node>q;
q.push(node(0, dis[0]));
while (!q.empty()) {
node cur = q.top();
q.pop();
if (vis[cur.id])continue;
vis[cur.id] = true;
for (int i = 0; i <= n; i++) {
if (mp[cur.id][i] == inf)continue; //無路
if (vis[i])continue;
if (dis[i] > mp[cur.id][i] + cur.dis) {
dis[i] = mp[cur.id][i] + cur.dis;
q.push(node(i, dis[i]));
}
}
}
}
int main() {
while (~scanf("%d%d%d", &n, &m, &e)) {
memset(mp, inf, sizeof(mp));
memset(dis, inf, sizeof(dis));
memset(vis, false, sizeof(vis));
while (m--) {
scanf("%d%d%d", &x, &y, &z);
if (z < mp[x][y]) //重邊
mp[x][y] = z;
}
scanf("%d", &x);
while (x--) { //置距起點為0
scanf("%d", &y);
mp[0][y] = 0;
}
dijkstra();
if (dis[e] == inf)puts("-1");
else printf("%d\n", dis[e]);
}
return 0;
}
(
插播反爬資訊)博主CSDN地址:https://wzlodq.blog.csdn.net
POJ-1062 昂貴的聘禮
Problem Description
年輕的探險家來到了一個印第安部落裡。在那裡他和酋長的女兒相愛了,於是便向酋長去求親。酋長要他用10000個金幣作為聘禮才答應把女兒嫁給他。探險家拿不出這麼多金幣,便請求酋長降低要求。酋長說:「嗯,如果你能夠替我弄到大祭司的皮襖,我可以只要8000金幣。如果你能夠弄來他的水晶球,那麼只要5000金幣就行了。「探險家就跑到大祭司那裡,向他要求皮襖或水晶球,大祭司要他用金幣來換,或者替他弄來其他的東西,他可以降低價格。探險家於是又跑到其他地方,其他人也提出了類似的要求,或者直接用金幣換,或者找到其他東西就可以降低價格。不過探險家沒必要用多樣東西去換一樣東西,因為不會得到更低的價格。探險家現在很需要你的幫忙,讓他用最少的金幣娶到自己的心上人。另外他要告訴你的是,在這個部落裡,等級觀念十分森嚴。地位差距超過一定限制的兩個人之間不會進行任何形式的直接接觸,包括交易。他是一個外來人,所以可以不受這些限制。但是如果他和某個地位較低的人進行了交易,地位較高的的人不會再和他交易,他們認為這樣等於是間接接觸,反過來也一樣。因此你需要在考慮所有的情況以後給他提供一個最好的方案。
為了方便起見,我們把所有的物品從1開始進行編號,酋長的允諾也看作一個物品,並且編號總是1。每個物品都有對應的價格P,主人的地位等級L,以及一系列的替代品Ti和該替代品所對應的"優惠"Vi。如果兩人地位等級差距超過了M,就不能"間接交易」。你必須根據這些資料來計算出探險家最少需要多少金幣才能娶到酋長的女兒。
Input
輸入第一行是兩個整數M,N(1 <= N <= 100),依次表示地位等級差距限制和物品的總數。接下來按照編號從小到大依次給出了N個物品的描述。每個物品的描述開頭是三個非負整數P、L、X(X < N),依次表示該物品的價格、主人的地位等級和替代品總數。接下來X行每行包括兩個整數T和V,分別表示替代品的編號和"優惠價格」。
Output
輸出最少需要的金幣數。
Sample Input
1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0
Sample Output
5250
分析:
把物品看作圖上的結點,互換關係看作邊,求最小花費也就是從起點到某一點的最短路徑。不過還需處理等級限制,只需要列舉等級區間,每次對滿足區間的點做dijkstra()即可。
比如起點等級是5,限制是3,那麼列舉的區間有[2,5]、[3,6]、[4,7]、[5,8]詳見程式碼。
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn = 102;
struct node {
int id, dis;
node(int a, int b) {
id = a, dis = b;
}
bool operator<(const node& a)const {
return a.dis < dis;
}
};
int n, m, x, y, z;
int mp[maxn][maxn], dis[maxn];
int lev[maxn], val[maxn];
bool tag[maxn], vis[maxn];
int dijkstra() {
memset(vis, false, sizeof(vis));
memset(dis, inf, sizeof(dis));
priority_queue<node>q;
dis[1] = 0;
q.push(node(1, dis[1]));
while (!q.empty()) {
node cur = q.top();
q.pop();
if (vis[cur.id])continue;
vis[cur.id] = true;
for (int i = 1; i <= n; i++) {
if (vis[i] || !tag[i])continue; //多一個判斷:是否在列舉區間內
if (dis[i] > mp[cur.id][i] + cur.dis) {
dis[i] = mp[cur.id][i] + cur.dis;
q.push(node(i, dis[i]));
}
}
}
int rtn = inf;
for (int i = 1; i <= n; i++)
if (rtn > dis[i] + val[i]) //記得加上結點權值
rtn = dis[i] + val[i];
return rtn;
}
int main() {
scanf("%d%d", &m, &n);
memset(mp, inf, sizeof(mp));
for (int i = 1; i <= n; i++) {
scanf("%d%d%d", &val[i], &lev[i], &x);
while (x--) {
scanf("%d%d", &y, &z);
mp[i][y] = z;
}
}
int ans = inf;
for (int i = 0; i <= m; i++) {
memset(tag, false, sizeof(tag));
for (int j = 1; j <= n; j++) { //列舉
if (lev[1] - m + i <= lev[j] && lev[1] + i >= lev[j])
tag[j] = true;
}
ans = min(ans, dijkstra());
}
printf("%d\n", ans);
return 0;
}
POJ-1511 Invitation Cards
Problem Description
In the age of television, not many people attend theater performances. Antique Comedians of Malidinesia are aware of this fact. They want to propagate theater and, most of all, Antique Comedies. They have printed invitation cards with all the necessary information and with the programme. A lot of students were hired to distribute these invitations among the people. Each student volunteer has assigned exactly one bus stop and he or she stays there the whole day and gives invitation to people travelling by bus. A special course was taken where students learned how to influence people and what is the difference between influencing and robbery.
The transport system is very special: all lines are unidirectional and connect exactly two stops. Buses leave the originating stop with passangers each half an hour. After reaching the destination stop they return empty to the originating stop, where they wait until the next full half an hour, e.g. X:00 or X:30, where ‘X’ denotes the hour. The fee for transport between two stops is given by special tables and is payable on the spot. The lines are planned in such a way, that each round trip (i.e. a journey starting and finishing at the same stop) passes through a Central Checkpoint Stop (CCS) where each passenger has to pass a thorough check including body scan.
All the ACM student members leave the CCS each morning. Each volunteer is to move to one predetermined stop to invite passengers. There are as many volunteers as stops. At the end of the day, all students travel back to CCS. You are to write a computer program that helps ACM to minimize the amount of money to pay every day for the transport of their employees.
Input
The input consists of N cases. The first line of the input contains only positive integer N. Then follow the cases. Each case begins with a line containing exactly two integers P and Q, 1 <= P,Q <= 1000000. P is the number of stops including CCS and Q the number of bus lines. Then there are Q lines, each describing one bus line. Each of the lines contains exactly three numbers - the originating stop, the destination stop and the price. The CCS is designated by number 1. Prices are positive integers the sum of which is smaller than 1000000000. You can also assume it is always possible to get from any stop to any other stop.
Output
For each case, print one line containing the minimum amount of money to be paid each day by ACM for the travel costs of its volunteers.
Sample Input
2
2 2
1 2 13
2 1 33
4 6
1 2 10
2 1 60
1 3 20
3 4 10
2 4 5
4 1 50
Sample Output
46
210
分析:
n站點m條公交路線,只從起點到終點(單向),求往返最小花費,來回往返兩次,把來的單向路弄一次,再把路反過來弄一次就行了。
注意資料較大用鄰接矩陣和long long。
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
#define inf 0x3f3f3f3f
typedef long long ll;
const int maxn = 1000006;
struct node {
int id, dis;
node(int a, int b) {
id = a, dis = b;
}
bool operator<(const node& a)const {
return a.dis < dis;
}
};
struct edge {
int from, to, w;
edge(int a, int b, int c) {
from = a, to = b, w = c;
}
};
vector<edge>e[maxn];
int t, n, m;
int dis[maxn];
int from[maxn], to[maxn], cost[maxn];
bool vis[maxn];
void dijkstra(int s) {
memset(dis, inf, sizeof(dis));
memset(vis, false, sizeof(vis));
dis[s] = 0;
priority_queue<node>q;
q.push(node(s, dis[s]));
while (!q.empty()) {
node cur = q.top();
q.pop();
if (vis[cur.id])continue;
vis[cur.id] = true;
for (int i = 0; i < e[cur.id].size(); i++) {
edge nex = e[cur.id][i];
if (vis[nex.to])continue;
if (dis[nex.to] > cur.dis + nex.w) {
dis[nex.to] = cur.dis + nex.w;
q.push(node(nex.to, dis[nex.to]));
}
}
}
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i++)e[i].clear();
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &from[i], &to[i], &cost[i]);
e[from[i]].push_back(edge(from[i], to[i], cost[i]));
}
dijkstra(1);
ll ans = 0;
for (int i = 1; i <= n; i++)
ans += dis[i];
for (int i = 0; i <= n; i++)e[i].clear();
for (int i = 0; i < m; i++) //反轉路的方向
e[to[i]].push_back(edge(to[i], from[i], cost[i]));
dijkstra(1);
for (int i = 1; i <= n; i++)
ans += dis[i];
printf("%lld\n", ans);
}
return 0;
}
原創不易,請勿轉載(
本不富裕的存取量雪上加霜)
博主首頁:https://wzlodq.blog.csdn.net
如果文章對你有幫助,記得一鍵三連❤