2020CSP-S1答案解析及總結

$Preparation$

回想以前的初賽經歷，小學五年級第一次去初賽，差0.5分進普及組複賽，六年級因為特殊原因缺席了
初一第一次擠進普及組複賽，初二初三普及組就比較順利了，初三擠進了提高組，分數還是挺懸的，講真對這次初賽沒有特別大的把握

於是9.17的時候就開始備戰初賽了，起初是做做歷年的NOIP，當然成績不是很理想，開始整理錯題複習知識點，寫了一個錯題本，說實話這個東西確實對我的幫助很大，特別是在修電腦的知識方面。。。

10/05開始正式天天做初賽，第一做了91.5（這輩子第一次初賽上90QwQ），第二次只有76，第三次又搞到了89，然後洛谷初賽做到了94，興奮地寫了題解，沒想到看的人挺多的QwQ

然後間歇的刷刷複賽題，就到考試日了。。。

---

$Feeling$

早上快八點出發去考點，到的時候和各位大佬複習了一下錯題（中間趁上廁所的時間甚至開了一把單挑？？？）
然後做的總的來說還可以吧，由於監考人員的失誤，大概開考5分鐘了才正式做題，不過無關緊要。
今年是第一年初賽用答題卡的呢，時間還是有點緊
閱讀2之前的題都很簡單，做得很快，閱讀2、3自閉了，完善1和2勉強能做到接近滿分吧。。。

今年的閱讀出奇的難，我這種菜雞估計只有80+了
如果覺得作者太菜了的大佬輕點噴，給我留點面子QwQ

---

$Solutions$

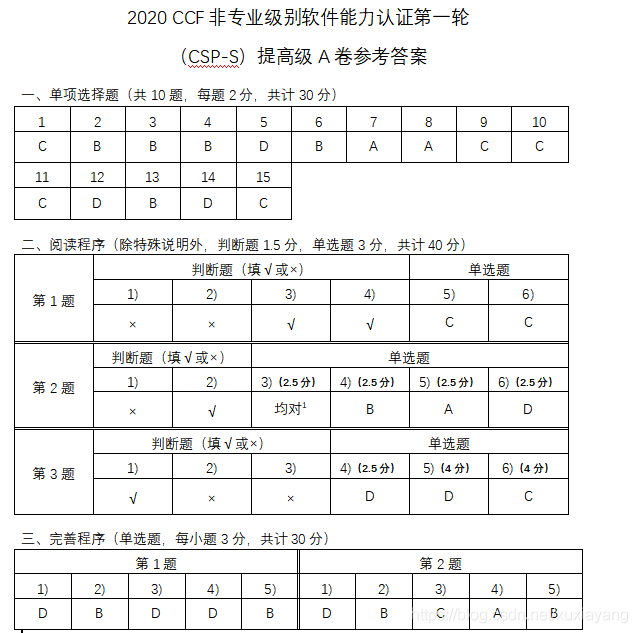
1~5

1：四個選項分別是，A 550、B 511、C 1024、D 558
2：定義題，沒啥好說的
3：8分鐘=480秒，每秒24幀，對應11520幀。每一幀都是$2048\times 1024$的畫素，且有32位元，32位元對應4B，相乘得到$11520\times 2048\times 1024\times 4B$，三項分別提取一個1024，得到$11.25\times 2\times 1\times 4GB=90GB$
4：如圖，最後棧中只剩下a和c，a是棧底，c是棧頂
5：A選項7和18會衝突，B選項7和18會衝突，C選項7和18會衝突。。。

6

單獨放出來不是因為它有多難或多重要，只是因為它佔了兩頁。。。

7~15

7：每個點和每條邊只會被遍歷一次
8：左右側各12各點，左側的每個點都能向右連12條邊，所以是$12\times 12=144$
9：常識題
10：可以暴力求解，也可以像我考場一樣列$CRT$
$\{\begin{array}{cc}x\equiv 2& (\mathrm{m}\mathrm{o}\mathrm{d}3)\\ x\equiv 3& (\mathrm{m}\mathrm{o}\mathrm{d}5)\\ x\equiv 4& (\mathrm{m}\mathrm{o}\mathrm{d}7)\end{array}$
$M=3\times 5\times 7=105$
$M_1=\frac{M}{3}=35$，$M_1{M}_1^{‘}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}3)$，得$M_1^{‘}=2$
$M_2=\frac{M}{5}=21$，$M_2{M}_2^{‘}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}5)$，得$M_2^{‘}=1$
$M_3=\frac{M}{7}=15$，$M_3{M}_3^{‘}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}7)$，得$M_3^{‘}=1$
所以該同餘方程組有最小正整數解
$x=(2M_1{M}_1^{‘}+3M_2{M}_2^{‘}+4M_3{M}_3^{‘})\mathrm{m}\mathrm{o}\mathrm{d}M$
$=(2\times 35\times 2+3\times 21\times 1+4\times 15\times 1)\mathrm{m}\mathrm{o}\mathrm{d}105$
$=(140+63+60)\mathrm{m}\mathrm{o}\mathrm{d}105$
$=263\mathrm{m}\mathrm{o}\mathrm{d}105$
$=53$
所以，$x\in (50,60)$
11：爬到第$i$層需要的體力為${\sum }_{i=1}^{i-1}10i=\frac{10(i^2-i)}{2}$，暴力帶入計算即可
12：如圖，畫出這個樹，然後寫出後序遍歷即可
13：每一個格子都能和九個格子連邊，這樣會多算一倍，所以是$\frac{16\times 9}{2}=72$
14：顯然
15：修電腦題，不多BB

閱讀1

1：可以等於1000
2：如果所有$d_i$都相等，會輸出-1
3：改過來之後如果是不上升序列一定會輸出-1，不改的話不一定
4：$i,j$都判斷一次$d_i<d_j$或$d_j<d_i$，其實就相當於判斷$d_i\ne d_j$
5：容易發現那個運算其實在二進位制下是不進位的
6：自己看，反例都舉在旁邊了

閱讀2

1：顯然是$[L,R]$
2：執行是不會出毛病的
3：答案應該是$lo{g}^{2}n$，所以四個選項都給分
4~6：作者都錯了，無法給出解析（我太菜了5555）

閱讀3

1：當兩串完全相同時，輸出0
2~6：作者不是蒙對了就是錯了，無法給出解析（我是真的菜555）

完善1

1：提示裡已經給出按照$\frac{w_j}{v_j}$從大到小排序，容易看出程式碼裡寫的是氣泡排序，所以當前面的權值比後面小時，交換，即$\frac{w_j}{v_j}\le \frac{w_{j+1}}{v_{j+1}}$，由於是分數運算，容易有精度問題，兩邊同時乘$v_j(v_{j+1})$，即可得到$w_j{v}_{j+1}\le w_{j+1}{v}_j$
2：若體積不夠或剛剛好，才需要考慮後面的
3：初始化
4：$print(w,v)$其實相當於輸出$\frac{w}{v}$，之前的$curW$都是可以完整選走的，由於輸出的時候除了$v[i]$，所以要乘下去，然後剩下的空間$（B-curV）$全部填上$w[i]$
5：如果能完全填滿，相當於輸出$curW$，即$\frac{curW}{1}$

完善2

1：可以帶入二進位制下的1010去試驗，發現只有$D$合法，其實其相當於$x-=x\&-x$，即$lowbit$
2：觀察發現$y$取走了$a$的低四位，那麼顯然$x$是要取走$a$的高四位
3：我也錯了QwQ
4：低位轉移
5：高位轉移

---

有問題和建議可以在下方留言