洛谷CSP-J/S2020初賽模擬部分題解

說明

試題來源於洛谷CSP-J/S2020初賽模擬試題。

選擇題

T1. 十進位制數114的相反數的8位元二進位制二補數是：（10001110）

【解析】整數的二進位制表示的最高位為符號位，用0表示「正」，用1表示「負」

• 正整數的二補數是其二進位制表示，與原碼相同。
• 負整數的二補數是將其原碼除符號位外的所有位取反（0變1，1變0，符號位為1不變）後加1。
  所以，114的二進位制表示為$(01110010{)}_2$，-114的二補數表示為$(10001110{)}_2$。

T3. 小A用字母$A$表示$1$，$B$表示$2$，以此類推，用$26$表示$Z$。對於27以上的數位，可以用兩位或者更長的字元來對應，例加$AA$對應$27$，$AB$對應$28$，$AZ$對應$52$，$AAA$對應$703$，…，那麼$BYT$字串對應的數位是（2022）

【解析】可將字串看做26進位制數，$A-Z$分別對應$1-26$，$AA$按照權值展開就是$1\times 26^1+1\times 26^0=27$，$AZ=1\times 26^1+26\times 26^0=26+27=52$，$AAA=1\times 26^2+1\times 26^1+1\times 26^0=703$，那麼$BYT=2\times 26^2+25\times 26^1+20\times 26^0=2022$

T5. 在一個長度為$n$的陣列中找到第$k$大的數位，平均的演演算法時間複雜度最低的是：$O(n)$

【解析】使用快速排序的思想實現。因為每次分割區完只需要繼續操作一邊，所以該演演算法的平均時間複雜度是$O(n)$。
用$T(n)$表示元素的比較次數，那麼平均情況下：

• 第一次劃分：$T(n)=T(\frac{n}{2})+n$
• 第二次劃分：$T(n)=T(\frac{n}{4})+\frac{n}{2}+n$
• 第三次劃分：$T(n)=T(\frac{n}{8})+\frac{n}{4}+\frac{n}{2}+n$
• $...$
• 最終： $T(n)=T(\frac{n}{n})+2+4+...+\frac{n}{4}+\frac{n}{2}+n=1+2+4+...+n$

上式是一個等比數列求和，公比為2，最終結果為：$T(n)=\frac{1-2\times n}{1-2}=2n$。

T6. 對於樹這種資料結構，正確的有：②③
①一個有n個頂點、n-1條邊的圖是樹。
②一個樹中的兩個頂點之間有且只有一條簡單路徑
③樹中一定存在度數不大於1的頂點
④樹可能存在環

【解析】
①錯誤，n-1條邊的圖可能不連通，也可能存在環，樹中不能有環。
④錯誤。
正確答案為：②③

T7. 博艾中學進行了一次資訊學會考測試，其優、良、及格、不及格的試卷數裡分別為10、13、14、5張。現在這些卷子混在一起，要將這些卷子按照等級分為4疊。分卷子的方法是，每次將一疊有不同等級答卷的卷子分為兩堆，使得這兩堆中沒有相同等級的卷子，然後可以再分，直到分為4疊。要分完這些卷子，至少需要（84）次「分卷子「的操作。注意：將一堆數量為n的卷子分成兩堆，就會產生n次「分卷子」的操作。

【解析】類似於將42張撲克牌按花色分成4堆，每張牌至少被分了兩次，所以答案為$42\times 2=84$

T10. 在一個初始長度為$n$的連結串列中連續進行k次操作，每次操作是讀入兩個數位$a_i$和$b_i$，在連結串列中找到元素為$a_i$的結點（假設一定可以找到），然後將$b_i$這個元素插入到這個結點前面。在最理想的情況下，連結串列存取的結點數量最少可能是（k）(不算將要插入的結點)。

【解析】最理想的情況就是每次都在第一個結點前插入$b_i$，此時連結串列表存取的總的結點數量為k。

T11. A班有5名風紀委員，B班有4名風紀委員，C班有3名風紀委員。現在需要這些同學中選取6名風紀委員巡邏，如果只關注各班派出的風紀委員人數，有（18）種不同的方案？

【解析】題目要求只關注各班派出的風紀委員人數，可以分情況討論：

• C班派出0名風紀委員，那麼A班派出的人數有4種可能，$2-5$
• C班派出1名風紀委員，那麼A班派出的人數有5種可能，$1-5$
• C班派出2名風紀委員，那麼A班派出的人數有5種可能，$0-4$
• C班派出3名風紀委員，那麼A班派出的人數有4種可能，$0-3$

所以一共有18種不同的方案

T13. 已知rand()可以生成一個0到32767的隨機整數，如果希望得到一個範圍在$[a,b)$的隨機整數，$a$別$b$均是不超過100的正整數且$a<b$，那麼可行的表示式是什麼?

【解析】舉例驗證即可，例如要生成的是$[1,10)$的隨機整數，可以通過$rand()\%9+1$得到，即$rand()\%(b-a)+a$

T14. 一個7個頂點的完全圖需要至少刪掉（15）條邊才能變為森林?

【解析】一棵樹也可以成為森林，所以將完全圖變為一棵樹，最少刪掉$21-6=15$條邊。

T15. 2020年8月，第（37）屆全國青少年資訊學奧林匹克競賽在（長沙）舉行。

【解析】常識題，NOI從1984年開始舉辦全國性競賽，所以到2020年應該是第37屆。

閱讀程式

T1.

#include <iostream>
using namespace std;
#define MAXN 20
int gu[MAXN][MAXN];
int luo(int n, int m) {
    if(n <= 1 || m < 2)
        return 1;
    if(gu[n][m] != -1)
        return gu[n][m];
    int ans = 0;
    for(int i = 0; i < m; i += 2)
        ans += luo(n - 1, i);
    gu[n][m] = ans;
    return ans;
}
int main() {
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < MAXN; i ++)
        for(int j = 0; j < MAXN; j ++)
            gu[i][j] = -1;
    cout << luo(n, m);
    return 0;
}

1. luo函數中，m的值不可能是奇數。（錯誤）
2. 將第11行的$<$改為$<=$，程式的輸出結果可能會改變。（正確）

【解析】i <= m會導致for迴圈中多一次遞迴呼叫，而當n <= 1 || m < 2時，luo函數返回1，從而導致結果發生改變。

3. 若將第8、9、13行刪除，程式的執行的結果不變。（正確）

【解析】第8、9、13行去掉，也就是不會記憶gu[i][j]，相當於沒有記憶化的深度優先搜尋，效率降低了，但不影響最後結果。

4. 在新增合適的標頭檔案後，將第19到21行替換為memset(gu, 255, sizeof(gu));可以起到相同的作用。（正確）

【解析】$255=(11111111{)}_2=0xFF$，相當於將gu陣列初始化為-1。

5. 輸入資料為4 8，則輸出為（8）。

【解析】畫遞迴樹模擬即可。

6. 最壞情況下，此程式的時間複雜度是（$O(m^{2}n)$）。

【解析】本題深度優先搜尋的遞迴樹的高度為$n$，每層的呼叫次數和$m$有關：

• m = 2，呼叫1次
• m = 4，呼叫2次
• m = 8，呼叫3次
  …
  總的呼叫次數$=1+2+3...$，近似於$m^2$，所以時間複雜度是$O(m^{2}n)$。

T2.

#include <cstdio>
using namespace std;
int n, m;
int f[101][101];
int F[101][101];
int main() {
    scanf("%d%d", &n, &m); //n的值在1到100之間
    memset(f, -1, sizeof(f));
    for(int i = 1; i <= m; i ++) {
        int u, v, w; //w的值在0到10000之間
        scanf("%d%d%d", &u, &v, &w);
        f[u][v] = f[v][u] = w;
    }
    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                if(f[i][k] != -1 && f[k][j] != -1)
                    if(f[i][j] == -1 || f[i][j] > f[k][j] + f[i][k])
                        f[i][j] = f[i][k] + f[k][j];
    int ans = 2147483647;
    for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++) {
                for(int x = 1; x <= n; x ++)
                    for(int y = 1; y <= n; y ++)
                        F[x][y] = f[x][y];
                F[i][j] = F[j][i] = 0;
                for(int x = 1; x <= n; x ++)
                    for(int y = 1; y <= n; y ++)
                        if(F[x][y] == -1 || F[x][y] > F[x][i] + F[i][y])
                            F[x][y] = F[x][i] + F[i][y];
                for(int x = 1; x <= n; x ++)
                    for(int y = 1; y <= n; y ++)
                        if(F[x][y] == -1 || F[x][y] > F[x][j] + F[j][y])
                            F[x][y] = F[x][j] + F[j][y];
                int res = 0;
                for(int x = 1; x <= n; x ++)
                    for(int y = 1; y <= n; y ++)
                        res += F[x][y];
                ans = min(res, ans);
            }
    printf("%d\n", ans);    
    return 0;
}

1. 14到16行，將外層則內層的迴圈變數依次訓整為i、j、k，程式的執行的結果不變。（錯誤）

【解析】Floyd多源匯最短路演演算法是利用動態規劃的思想，列舉每一個點作為中轉點，來鬆弛任意兩點的路徑。所以第一重回圈是列舉中轉點，迴圈變數依次訓整為i、j、k後，19行程式碼也要隨之修改。

2. 這個程式的時間複雜度和m無關。（錯誤）

【解析】難道輸入也算？

3. 20行的ans如果初始化為$10^7$時,可能無法得到正確結果。（正確）

【解析】 ans為任意兩點最短距離之和的最小值，一共有$\frac{(n-1)\times n}{2}$條邊，每條邊的權值最大為10000，所以最大值可能超過$10^7$

4. 若將第27到30行的部分和31到34行的兩個部分互換，程式的執行的結果不變。（正確）

【解析】程式的第26行F[i][j] = F[j][i] = 0;，作用是將i、j兩點用權值為0的邊連線起來，相當於合併了兩點，然後使用i、j兩點嘗試鬆弛其它點之間的最短路徑。所以，先使用i點或是j點對最終結果沒有影響。

5. 若資料如資料為下面的值，則輸出結果為（14）。

4 5
1 2 3
1 3 6
2 3 4
2 4 7
3 4 2

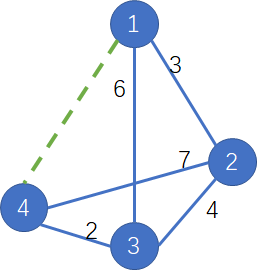
【解析】如下圖所示，在1、4之間連線一條權值為0的邊，此時個點之間的最短距離：

• f[1][2] = 3
• f[1][3] = 2，經過4點中轉。
• f[1][4] = 0
• f[2][3] = 4
• f[2][4] = 3 ，經過1點中轉
• f[3][4] = 2

最短距離之和為14

T3.

#include <iostream>
using namespace std;
#define MOD 19260817
#define MAXN 1005
long long A[MAXN][MAXN] = {0}, sum[MAXN][MAXN] = {0};
int n, m, q;
int main() {
    A[1][1] = A[1][0] = 1;
    for(int i = 2; i <= 1000; i ++) {
        A[i][0] = 1;
        for(int j = 1; j <= i; j ++)
            A[i][j] = (A[i - 1][j] + A[i - 1][j - 1]) % MOD;
    }
    for(int i = 1; i <= 1000; i ++)
        for(int j = 1; j <= 1000; j ++)
            sum[i][j] = (sum[i - 1][j] + sum[i][j - 1]
                - sum[i - 1][j - 1] + A[i][j] + MOD) % MOD;
    int q;
    cin >> q;
    while(q --) {
        int n, m;
        cin >> n >> m;
        cout << sum[n][m] << endl;
    }
    return 0;
}

1. 當i<=j時，A[i][j]的值是0。（錯誤）

【解析】當i == j時，A[i][j] = 1。

2. 當i>j時，A[i][j]的值相當於從i個不同元素中取出j個元素的排列數。（錯誤）

【解析】楊輝三角（帕斯卡三角）求組合數。

3. sum[i][j]的值（$1<j\le 1000$）不小於sum[i-1][j-1]的值。(錯誤)

【解析】sum[i][j]為矩陣的字首和，但是，因為在計算過程中需要對MOD求餘數，所以sum[i][j]的值不一定大於sum[i-1][j-1]的值。

4. 若將第12行改為A[i][j]=(A[i-1][j] + A[i-1][j-1] + MOD) % MOD;，程式的執行結果不變。（正確）

【解析】加法的同餘性質。

5. A[i][j]（$1\le i\le 10,1\le j\le 10$）的所有元素中，最大值為是（）。

【解析】最大值為$C_{10}^5=252$。

6. 若輸入下列資料，則輸出為（50）

1
5 3

【解析】求楊輝三角前5行3列的子矩陣的和，答案為50。

完善程式

T1. （封禁xxs）現有$n$個xxs（編號為1到n），每個xxs都有一個關注者，第$i$個xxs的關注者是$a_i$。現在管理員要將其小的一些xxs的賬號封禁，但需要注意的是如果封禁了第$i$個人，那麼為了不打草驚蛇，就不能封禁他的關注者$a_i$。現在想知道最多可以封禁多少個xxs。

輸入第一行是一個不超過300000的整數$n$，第二行是$n$個$1$到$n$的整數表示$a_i$。

輸出一行，一個整數表示答案。

#include <cstdio>
using namespace std;
#define MAXN 300005
int n, ans = 0, a[MAXN], in[MAXN] = {0};
bool vis[MAXN] = {0};
void dfs(int cur, int w) {
    if(vis[cur])
        return;
    vis[cur] = true;
    if(w == 1) ans ++;
    ①
    if(②)
        dfs(a[cur], ③);
}
int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) {
       scanf("%d", &a[i]);
       in[a[i]] ++;
    }
    for(int i = 1; i <= n; i ++)
        if(!in[i]) ④;
    for(int i = 1; i <= n; i ++)
        if(⑤) dfs(i, 0);
    printf("%d\n", ans);
   return 0;
}

【解析】題目中提示每個xxs只有一個關注者，a[i]表示第i個xxs的關注者，即a[i]是i的粉絲。in[a[i]]表示a[i]的入度，可以理解為a[i]的粉絲個數。那麼如果in[a[i]]不為0，為了不打草驚蛇，就不能封禁a[i]。

• 空①，分析第10行，if(w == 1) ans ++;，表示封禁一個xxs。封禁後，這個xxs的關注者（a[cur]）的粉絲數量應該減少一個，所以應填入in[a[cur]]--。
• 空②，封禁cur後，如果cur的關注者的粉絲為0，或者cur的粉絲數量為0，那麼繼續對cur的關注者進行處理，所以此空應判斷in[a[cur]] == 0 || w == 1。
• 空③，如果w == 1，那麼對cur的關注者不能夠直接封禁，那麼遞迴處理時，w = 0；如果w == 0 && in[a[cur]] == 0，此時對a[cur]可以封禁，w = 1。所以此空應填入1 - w。
• 空④，如果i的粉絲為0，可以直接封禁，此空應填dfs(i, 1)。
• 空⑤，如果i還沒有處理，即vis[i]為0，所以此空應填!vis[i]。

T2. 大水