2019-2020 ICPC Asia Hong Kong Regional Contest B D E G J

B.Binary Tree

題意

給定一個二元樹，每次Alice和Bob可以取走一個完全二元樹，直到完全不能取為止，第一個不能取得為輸，求那個輸

思路

這是一個博弈論，我們先分析他最基礎的性質，一個完美二元樹是2^k -1，很明顯他是一個奇數，最小的完美二元樹就是一個葉節點，所以最終結果必然是全部取完的，且每次取必然是奇數，所以我們就能得到如果是奇數，那麼Alice 獲勝，反之Bob

程式碼

#include<iostream>

using namespace std;

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int n;
        scanf("%d",&n);
        for(int i = 1;i<n;i++){
            int a,b;
            scanf("%d%d",&a,&b);
        }
        if(n & 1) puts("Alice");
        else puts("Bob");
    }
    
    return 0;
}

D Defining Labels

題意

給定一個k，其中 10 - k <= x <= 9,他的表現形式為a,b,c,d,e,f,aa,ab,ac,ad,ae,af……ff,給定k求第i個這樣的數

思路

我們可以把它看做k進位制，但是從1開始，所以給他減1即可

程式碼

#include<iostream>
#include<vector>
using namespace std;
 
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        vector<int > ans;
        int k,n;
        scanf("%d%d",&k,&n);
        int u = 9 - (10 - k) + 1;
        while(n){
            n -= 1;
            int t = n % u;
            ans.push_back(t + 10 - k);
            n /= u;
        }
        for(int i = ans.size() - 1;i >= 0;i--){
            printf("%d",ans[i]);
        }
        puts("");
    }
    
    return 0;
}

E Erasing Numbers

題意

給定一個1-n的排列，對於連續的三個數，可以刪除它的最小值和最大值，求最後可以剩下的數

思路

對於要保留的數來說，剩餘的數我們無需關注他本身的大小，只需關注和這個數的大小，所以剩餘的數用0和1表示，0表示比他小的 1表示比他大的。保留這個數也就是最後要剩餘一個01，在刪除的時候如果三個數有01，那麼必然刪除一個0和1，我們只需0和1的個數相等（因為必然有0 1 連線的地方，那樣就能一次次刪除一個 0 1），所以問題就轉換為怎樣刪除才能使0 1 個數相等，只有使用000，111 刪除兩個0 或 1才能使0和1的個數有可能相等相等（也就等價於0 1 中個數多的只刪除這個數，能否小於等於個數小的那個數，因為0和1都同時是偶數或奇數，刪除多必然能保證相等），所以根據這個規律我們對於每個數分別處理時間複雜度為 $\mathcal{O(n^2)}$
(對於11011這種情況我們可以先刪去一個0 1 在處理)

程式碼

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int N = 5010;
int a[N];
int n;
bool check(int x){
    bool v = a[x] < (n + 1)/2;
    int k = abs(a[x] - 1 - (n  - a[x])); // 多的比少的 多的個數
    // cout<<k<<endl;
    int t = 0;
    for(int i = 1;i <= n;i++){
        if(i == x) { // 如果中間穿插這個數，兩個型別相同的必然會使這個數被刪除
            t = 0;
            continue;
        }
        if((a[i] < a[x]) != v){ // 和多的數是一個型別的
            t++;
            if(t == 3){  // 等於三個刪除兩個
                t = 1;
                k -= 2;
            }
        }
        else t = max(t - 1,0); // 如果兩個不同的數在一起可以嘗試先刪除這個使他前面的能夠組成 相同型別即那種特殊情況
    }
    return k <= 0;
}
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i = 1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        for(int i = 1;i <= n;i++){
            if(check(i)) printf("1");
            else printf("0");
        }
        puts("");
    }
    
    return 0;
}

G Game Design

題意

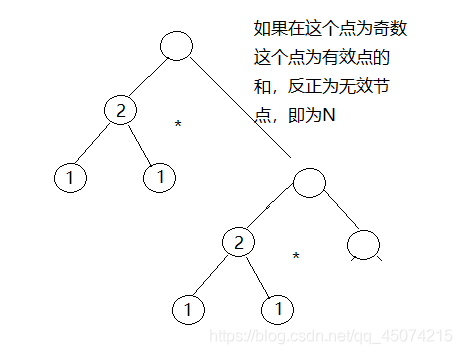
有一顆樹它的葉子節點會被敵軍攻擊，需要建立防禦系統，防禦系統會抵禦所有的在這個節點的攻擊，在不同的節點建立防禦系統的代價是有可能不同（是由自己定義的），目的是守護最後根節點的安全，並且根節點也可以建立防禦系統。給定一個方案數，求自己設計一個樹，根節點為1號點，每個點防禦的代價自己設定，需要滿足最小代價的方案數為給定方案數

思路

我們可以想象一下對於一個數，假定為二元樹，在這個點的方案數就等於左子數的方案數 * 右子數的方案數 + （根節點是否有方案數有則為1反之為0），所以根據這個性質我們就能一個給左子數建立方案數為2的，如果這個方案數為奇數那麼給根節點建立1，對右子數遞迴處理

在這裡插入圖片描述

程式碼

#include<iostream>

using namespace std;
const int N = 1e5+10;
int h[N];
int c[N];
int cnt = 2;
int dfs(int n,int u,int fa){
    h[u] = fa;  // 這個節點的父節點
    if(n == 1){ // 只剩一個節點 這個節點建立一個權重為1
        c[u] = 1;
        return 1;
    }
    // 左子數建立2的方案數
    c[cnt++] = 1,h[cnt - 1] = cnt + 1; 
    c[cnt++] = 1,h[cnt - 1] = cnt;
    c[cnt++] = 2,h[cnt - 1] = u;
    // 方案數為奇數 給根建立1的方案數  遞迴處理右子數
    if(n & 1) 
    {
        c[u] = dfs(n / 2,cnt++,u) + 2;
        return c[u];
    }
    else{
        c[u] = N;
        return dfs(n / 2,cnt++,u) +2;
    }
}
int main(){
    int n;
    scanf("%d",&n);
    if(n == 1){ // 特例
        puts("3");
        puts("1 1");
        puts("5 1 1");
        return 0;
    }
    dfs(n,1,-1);
    cout<<cnt - 1<<endl;
    for(int i = 2;i<cnt;i++){
        printf("%d ",h[i]);
    }
    puts("");
    for(int i = 1;i<cnt;i++){
        printf("%d ",c[i]);
    }
    return 0;
}

J Junior Mathematician

題意

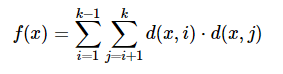
在這裡插入圖片描述
其中d(x,i) 表示x的第i位對應的數
對於這個方程我們大概的理解就是第i位乘上它後面所有位對應的數位的和，求在[l,r]存在多少個數位的和為等於x本身

思路

很明顯這是一個數位dp，我們需要預處理第i位選擇哪個值，對應的字首和，以及這個值本身和f(x)那麼我們需要很多的記憶體，5000 * 10 * 60 * 60 * 60 = 10¹⁰ 顯然是不夠的我們需要對陣列進行優化，首先f(x) == x 我們可以優化為一個陣列，用dfs來列舉可以在優化一維，也就變為5000 * 60 * 60 = 1.8 * 10⁷ 是足夠的，在時間上5000 * 10 * 60 * 60 = 1.8 * 10⁸
有點卡常

程式碼

#include<iostream>
#include<cstring>
#include<cmath>

using namespace std;
const int N = 5010,M = 65,mod = 1e9 + 7;
int f[N][M][M];
char l[N],r[N];
int dight[N];
int p[N];
int m;
int dfs(int pos,int v,int sum,bool limit){ // v = f(x) - x,sum 各個位置之和
    if(pos == 0) return v == 0; // 邊界
    if(!limit && f[pos][v][sum] != -1) return f[pos][v][sum];
    int up = limit?dight[pos]:9;
    long long ans = 0;
    for(int i = 0;i <= up;i++){
        int vv = (v + (sum * i - i * p[pos - 1])%m + m)%m;
        ans += dfs(pos - 1,vv,(sum + i)%m,limit&&i == up);
    }
    ans %= mod;
    if(!limit) f[pos][v][sum] = ans;
    return ans;
}
int solve(char *s,int len){
    for(int i = 1,j = len;i <= len;i++,j--){
        dight[i] = s[j];
    }
    return dfs(len,0,0,true);
}

int main(){
    int T;
    scanf("%d",&T);
    p[0] = 1;
    while(T--){
        scanf("%s%s%d",l + 1,r + 1,&m);
        int n = strlen(l + 1),k = strlen(r + 1);
        for(int i = 1;i <= n;i++) l[i] -= '0';
        for(int i = 1;i <= k;i++) r[i] -= '0';
        // 在對第x位的數位處理的時候使用
        for(int i = 1;i <= k;i++)
            p[i] = 1ll * p[i - 1] * 10 % m;
        // 初始化
        for(int i = 1;i <= k;i++){
            for(int j = 0;j < m;j++)
                for(int u = 0;u < m;u++)
                    f[i][j][u] = -1;
        }
        int t = -1;
        for(int i = n;i >= 1;i--){
            l[i] += t;
            if(l[i] < 0) l[i] += 10;
            else break;
        }
        printf("%d\n",(solve(r,k) - solve(l,n) % mod + mod)%mod);
    }
    
    return 0;
}