星星之火-9:詳解通道特性與奈奎斯特定理和夏農定理
奈奎斯特定理和夏農定理,結論很簡單,但理解起來有點費勁,特別是結論背後的原因,本文在不進行數學推導的情況下,對此進行詳細的拆解。
目錄
第1章 傳輸通道
1. 1 通道的定義與分類
資料傳輸通道是指為資料訊號傳輸提供的通路。
(1)狹義通道,僅指傳輸媒介本身,能夠傳輸訊號的任何抽象的或具體的通路,如電纜、光纖、微波、短波等。
(2)廣義通道,包含傳輸媒介和完成各種形式的訊號變換功能的傳送及接收裝置,可看成是一條實際傳輸線路及相關裝置的邏輯部件。
從不同角度對通道有多種分類方法:
(1)按照允許的訊號的型別分為模擬通道和數位通道。
模擬通道只允許傳輸波形連續變化的模擬訊號,通訊品質可用失真和輸出訊雜比來衡量。
數位通道只允許傳輸離散的數位訊號,數位通道的特性可用差錯率及差錯序列的統計特性來描述。
模擬資料和數位資料都可以用模擬訊號或數位訊號來表示,因而無論信源產生的是模擬資料還是數位資料,在傳輸過程中都可以用適合於通道傳輸的某種訊號形式來傳輸。
(2)按通道的使用方法分為專用通道和公共交換通道。
專用通道是指連線兩點或多點的固定線路,
公共交換通道是一種通過交換機轉接可為大量使用者服務的通道。
(3)按資料傳輸的同步方式分為同步通道和非同步通道。
(4)按通道傳輸的資訊複用形式分為分頻多工通道和分時多工通道。
(5)按照通道採用的傳輸媒介分為有線通道和無線通道。
有線通道主要有四類。即明線(open wire)、對稱電纜(Symmetrical cable)、同軸電纜(coaxial cable)和光纖(Optical fiber)。
有線通道:以導線(雙絞線或者光纖等)為傳輸媒質,訊號沿導線進行傳輸,訊號的能量集中在導線附近,因此傳輸效率高,但是部署不夠靈活。訊雜比高、頻帶資源窄、存在回波和非線性失真。


無線通道:是對無線通訊中傳送端和接收端之間通路的一種形象比喻,對於無線電波而言,它從傳送端傳送到接收端,其間並沒有一個有形的連線,它的傳播路徑也有可能不只一條,因此無線通道,通常是指空氣,又稱為自由空間,傳輸的訊號是無線電磁波。
1.2 通道的衰減特性
無論是電訊號、還是光訊號、還是無線電磁波訊號,通過物理傳輸通道時候,其幅度會隨著傳輸的距離的增加而衰減。
有線通道的衰減或損耗:

有線通道只有路徑衰減,不存在多徑衰減與地形陰影衰減。
無線通道的衰減或損耗:
在無線通訊領域,衰落是指由於通道的變化導致接收訊號的幅度發生隨機變化的現象,即訊號衰落。
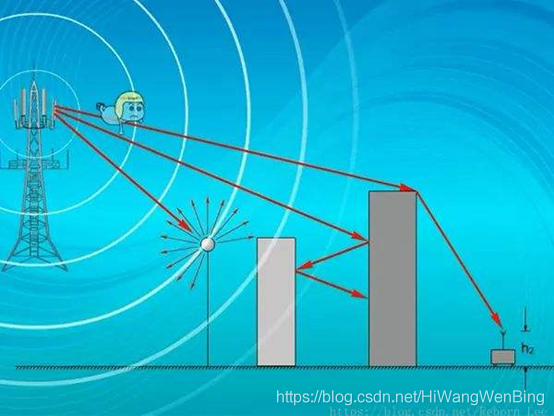
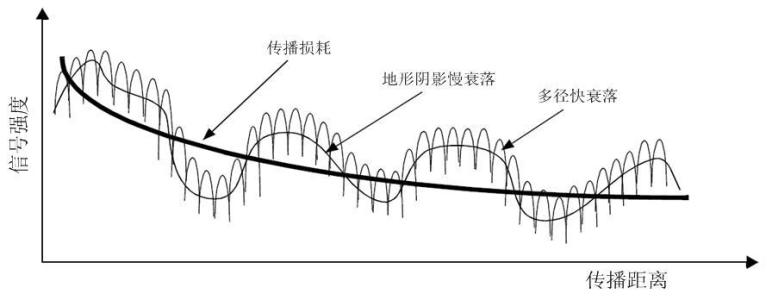
路徑損耗,或稱傳播損耗,指訊號在空間傳播所產生的損耗,是由發射功率的輻射擴散及通道的傳播特性造成的
多徑衰落:是指在微波訊號的傳播過程中,由於受地面或水面反射和大氣折射的影響,會產生多個經過不同路徑到達接收機的訊號,通過向量疊加後合成時變訊號.多徑衰落可分為平衰落和頻率選擇性衰落
陰影衰落: 行動通訊中,由障礙物阻擋造成的陰影效應,接受訊號強度下降,但該場強中值隨地理改變緩慢變化,又稱慢衰落。
1.3 通道頻率特性與頻寬
是指傳輸通道,對不同頻率的訊號的衰減特性。
(1)有線通道:
任何有線通道,都相當於一個低通濾波器,只能允許小於一定頻率的訊號通過,而這個頻率,就是通道的截止頻率。
由於有線通道,都允許直流訊號的通過,通道的頻寬,也是截止頻率。
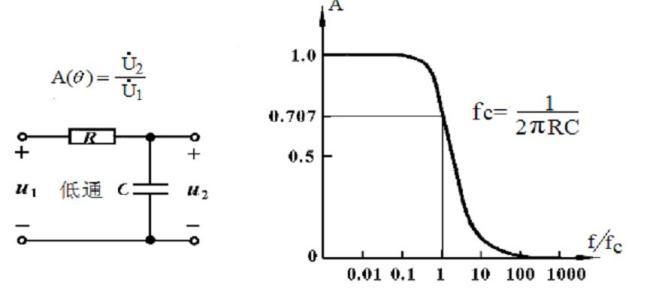
截止頻率:當保持輸入訊號的幅度不變,改變頻率使輸出訊號降至最大值的0.707倍,即用頻響特性來表述即為-3dB點處即為截止頻率,它是用來說明頻率特性指標的一個特殊頻率
截止頻率或通道頻寬表明:有線通道並不能傳輸所有頻率的電訊號,因此有限通道的頻寬是有限的!
(2)無線通道:
無線通道傳輸的是電磁波,其頻率是一個連續的電磁波譜:

可以看出,理論上講,無線通道的頻寬是無限的,可以傳輸任何頻率的電磁波!
注意:
這裡的頻寬,是通道的頻寬,是從直流分量0頻率到通道的最高頻率、截止頻率,而不是人為定義的一段電磁波譜。
第2章 數位通訊與位元率、波特率
數位通訊已經成為現代通訊的主流,而數位訊號通過通道進行傳輸一個個代表0或1的電訊號,能夠完整代表0或1的電訊號,稱為符號或波。表示0和1的電訊號的符號有各種方法:
詳見:《圖解通訊原理與案例分析-2:如何用電訊號來表示和傳輸0和1,遠遠比我們想象的要複雜得多》
https://blog.csdn.net/HiWangWenBing/article/details/107897420
2.1. 代表二進位制的「電」符號symbol
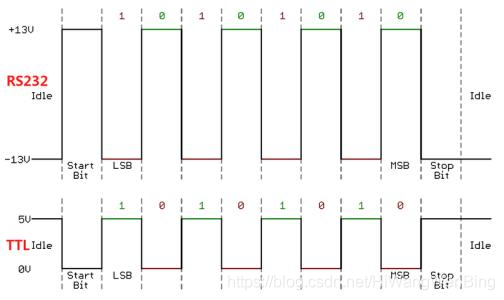
(1)用低電平表示0,1電平表示0, 在一個時鐘週期內的高電平或低電平訊號,就是一個符號。
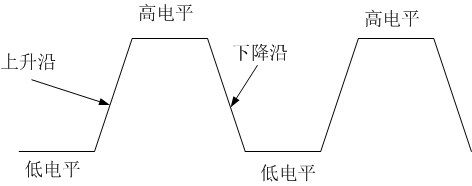
(2)用正電平表示0,或負電平表示1. 在一個時鐘週期內的負或正電平訊號,就是一個符號。
(3)二進位制幅度2-ASK

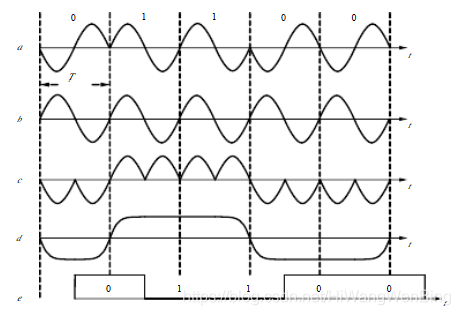
n個幅度為A的載波訊號整體,就是一個符號,代表0或1.
N= 1時,為最大符號率。
(4)2-PSK


N個完整的相位為 0°的電磁波訊號表示0. N=1或2或。。。N的大小取決於傳輸的二進位制的速率。
N個完整的相位為180°的電磁波訊號表示1. N=1或2或。。。N的大小取決於傳輸的二進位制的速率。
N= 1時為最大符號率。
(5)Q-PSK

四個相位不同的波形,用來傳遞0或1. 每個波形就是一個符號。
N個完整載波週期的波形表示00,N=1或2或。。。N的大小取決於傳輸的二進位制的速率,
N個完整載波週期的波形表示01,N=1或2或。。。N的大小取決於傳輸的二進位制的速率。
N個完整載波週期的波形表示10,N=1或2或。。。N的大小取決於傳輸的二進位制的速率。
N個完整載波週期的波形表示11,N=1或2或。。。N的大小取決於傳輸的二進位制的速率。
N= 1時為最大符號率。
2.2 符號率、波特率、位元率
符號=波:傳遞二進位制0和1的完整的電訊號。
符號率=波特率:單位時間傳遞的完整的符號的個數。
位元率:單位時間傳遞的完整的二進位制的個數。
如果每個符號代表1個位元,位元率= 符號率=波特率 ,比如單位時間能夠傳遞1K個符號,就意味著能夠傳遞1K個二進位制位元。
如果每個符號代表2個位元,位元率/2= 符號率=波特率,比如單位時間能夠傳遞1K個符號,就意味著能夠傳遞2K個二進位制位元。
如果每個符號代表3個位元,位元率/3= 符號率=波特率. 比如單位時間能夠傳遞1K個符號,就意味著能夠傳遞3K個二進位制位元。
2.3. 最大符號率、 最大符波特率、 最大符位元率
由於通道是有最大頻寬的,即有截止頻率的。
因此,無論通過電平訊號傳遞0和1,還是通過一定頻率的正弦波/餘弦波訊號傳遞0或1,只要電訊號,在通道中進行傳輸,就意味著,單位時間傳遞的符號或波的個數是受限的,也就是傳遞的二進位制位元是受限的!
(1)攜帶二進位制位元的符號是特定頻率的正弦波
如下的二進位制幅度2-ASK為例:

N個完整的載波正弦波表示0或1.
當N1=1是,表示一個完整的載波表示0或1,此時得到傳輸位元的最大上限。
如果傳送的位元率再繼續增大,那麼在單個二進位制位元週期內,只能傳遞不完整的載波訊號,這樣就會導致傳輸出錯。
因此,在這種情況下,載波訊號(符號)就是通道的頻寬,單位時間傳遞的完整波形的個數,就是傳遞的二進位制位元的上限。
(2)攜帶二進位制位元的符號的方波訊號
此時方波訊號週期,就是二進位制位元的週期,方波訊號的頻率,就是二進位制位元的速率。
如果方波訊號的頻率無限大,那麼傳遞的二進位制位元的速率就無限大。

然而,根據傅立葉變換,方波訊號實際上是由無限個具有諧波關係的正弦波訊號疊加而成的,且基波的頻率與方波的頻率是相同的,因此,如果傳播方波訊號的通道是有截止正弦波頻率的,那就意味著,方波符號的波特率也是受限制的,不能超過通道的截止頻率。

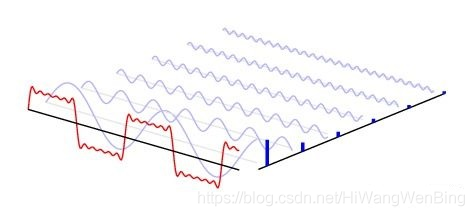
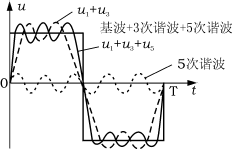
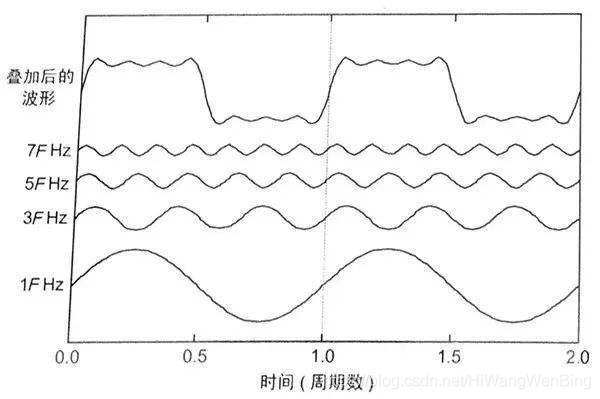
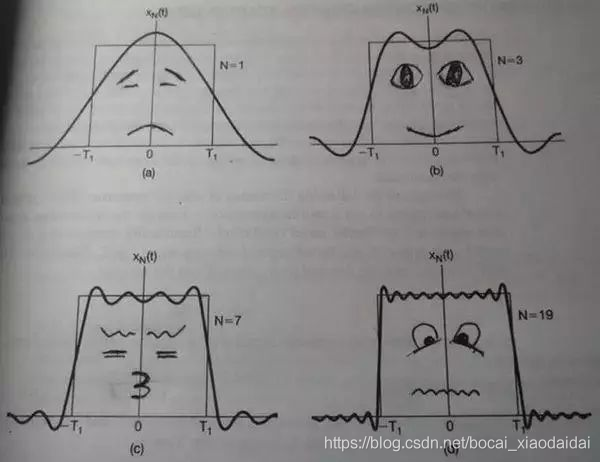
從上圖可以看出,方波訊號的週期與基波分量的週期是一致的,只是波形不同而已,通過基本分量,基本上可以還原方波訊號!
當弱通道的截止頻率,低於基波分量的頻率,也就是通道把基波分量也過濾掉了,那麼就很難還原方波訊號了,也就是說,方波訊號同構該通道,就會變形!
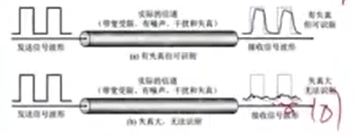
實際上,方波訊號包含了高電平與低電平訊號,相當於一個方波訊號同時攜帶了0和1的兩個符號,且不能分離,在這種情況系下,相當於二進位制的符號率是方波訊號的符號率的2倍。
當然,這種方式傳遞二進位制是沒有意義的,因為同時攜帶0和1,且0和1無法分離,對於接收端而言,無法區分0或1,但至少表明了一點,符號率可以做到是頻寬的兩倍!!!
那麼如何解決詞問題呢?
- 通過方波訊號的上升沿與下降沿傳遞0或1訊號
這樣的話,這個方波訊號/符號,就只能攜帶一個0或一個1。在這種情況下,方波訊號的符號是頻寬的1倍。
也就是說,在頻寬確定的情況下,如果通過方波訊號傳遞資訊,是要犧牲二進位制的位元率的。
當然,通過方波訊號傳遞二進位制也是能帶來好處的:就是在傳遞資料的同時,也可以傳遞了時鐘訊號。
廣泛應用在乙太網中的曼切斯特編碼,就是利用這個特性:犧牲二進位制位元符號傳輸率,獲得訊號傳輸的時鐘。
- 分離方波訊號中的符號0和1,這就需要用矩形脈衝訊號!
(3)攜帶二進位制資訊的雙極性矩形脈衝訊號
規定對映:0 -》 1, 1=》 -1;
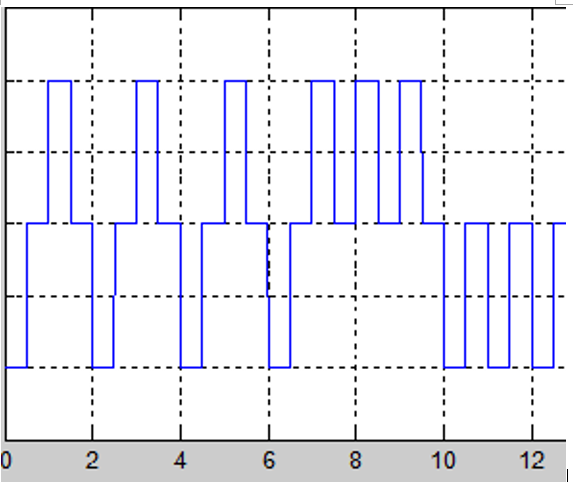
雙極性矩形脈衝訊號的週期,就是二進位制位元的週期!
雙極性脈衝訊號是指通道傳輸中常用的一種碼形,它由一個正的振幅表示其一種狀態,而由負的振幅表示其另一狀態的數位訊號。
矩形脈衝訊號又稱為為「門」訊號、衝擊脈衝訊號等,它們相關,但由不完全一樣。通過他們頻譜的演變,可以看出脈衝訊號與頻寬的定性關係:
- 週期無窮小的衝激訊號及其傅立葉變換分析
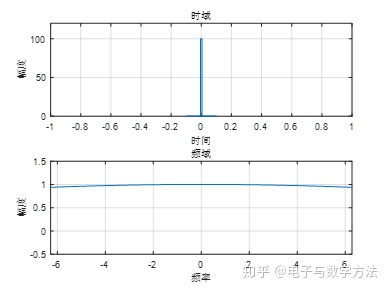
衝激訊號訊號的週期T無限接近於0,其理論頻譜和頻寬 B都 無限大。
衝激的頻譜是一條直線,幅值為常數1,頻率範圍為無窮,即包好所有的頻率成分,且每個頻率分量的權重都是接近相等的。
因此,傳輸衝激訊號的頻寬必須是無窮的!
- 門訊號及其傅立葉變換分析
衝激訊號的時間寬度趨於零,假設門訊號的時間寬度為T,則我們可以推測門訊號的頻譜包含了許多成分,但不至於像衝激函數的頻譜,包含所有的頻率分量。門訊號的頻譜符合sinc函數的分佈規律:
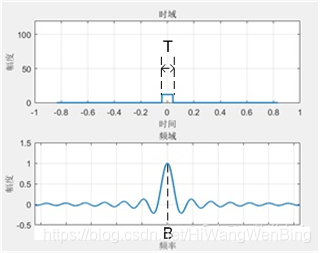
定性的來看,
門訊號的持續時間越短,越接近衝激訊號,內涵的每個頻率分量的權重越接近相同。
門訊號的持續時間T越長,即頻率F越小,其頻譜特性越接近sinc,內涵的每個頻率分量的權重越符合上圖的sinc函數的規律,高頻分量的權重越小, 且基波頻率B的值就越小。
門訊號的持續時間T越短,即頻率F越大,其頻譜特性越接近衝激訊號,內涵的每個頻率分量的權重越符合上圖的衝激訊號函數的規律,高頻分量的權重越大, 且基波頻率B的值就越大。
在上圖中,門訊號頻率f(F=1/T)與其頻譜中的基波訊號的頻率B是一種線性關係:F=2B.
這個結論非常重要!這是奈奎斯特(Nyquist)準則的背後原因!
上述是從定性的角度理解通道頻寬與最大傳遞的二進位制之間的定性關係。
有沒有一種方法,定量研究通道的頻寬與傳遞的二進位制位元率的關係呢?到底是什麼數學關係呢?以及其別後的原理是什麼呢?
這就涉及到奈奎斯特定理和夏農定理。
第3章 奈奎斯特(Nyquist)準則
(1)什麼是奈奎斯特(Nyquist)第一準則
奈奎斯特定理給出了理想的無噪聲通道,資訊傳送速率的上限(位元每秒)和頻寬的關係。
奈奎斯特定理可以解釋現代各種通訊通道由於頻寬不同,所支援的通道最大吞吐量的不同。
1924年,奈奎斯特(Nyquist)就推匯出在理想低通訊道下的最高碼元傳輸速率的公式:
Bmax = 2W(band)
其中W是理想低通訊道的頻寬,單位為赫茲;
Baud是波特,即碼元傳輸速率的單位,1波特為每秒傳送1個碼元。
Bmax為最高波特率,是頻寬的2倍!
當通道頻寬為B時,傳送的最大符號速率是2B,超過2B,接收方就會產生碼間干擾,不能恢復出你原來傳送的資訊。
這就是奈奎斯特(Nyquist)第一準則。
(2)這裡可能會有一個疑問:既然通道都是無噪聲了,那為什麼不是傳送方發多快,接收方就能收多快呢?
這個問題答案是:實際通道是有頻寬的,通道是一個低通濾波器,能夠濾除高頻訊號,即阻止高頻訊號的通過,高頻訊號是無法通過通道的!
(3)第二個可能的疑問是:為什麼是2倍的關係?
只所以最大波特率與頻寬是2倍關係,主要原因是承載二進位制位元訊號「門」訊號,而不是「方波」訊號。
如果承載二進位制位元訊號是方波訊號,其週期為T, 半週期為T/2,最大波特率與頻寬是1倍關係。
如果承載二進位制位元訊號是門訊號,其週期為T, 最大波特率F=1/T, 其與頻寬B是2倍關係。即F<=2B.
因此,如果傳送的波特率大於2B, 即每個符號的傳送時間小於T, 其內含的基波分量的頻率就會增加,大於原先的2B,如果通道頻寬不變,導致基波訊號無法通過該低通濾波器通道。
(4)波特率與位元率的關係
需要注意的是:奈氏準則並沒有對二進位制位元的傳輸速率(b/s)給出限制。
要提高資訊的二進位制位元傳輸速率,就可以使每一個傳輸的碼元或訊號波能夠代表更多的位元的資訊。這這個過程稱為編碼與調變。
如2-ASK: 每個符號傳遞1個位元
如2-PSK: 每個符號傳遞1個位元
如Q-PSK: 每個符號傳遞2個位元
如8-PSK: 每個符號傳遞3個位元
如16-QAM: 每個符號傳遞4個位元
如32-QAM: 每個符號傳遞5個位元
如64-QAM: 每個符號傳遞6個位元
如128-QAM:每個符號傳遞7個位元
如256-QAM:每個符號傳遞8個位元
如N-QAM:每個符號傳遞n個位元
波特率與位元率的關係為:
![]()
(5)奈奎斯特(Nyquist)準則位元率的表示式
![]()
如果N=2, 位元率=2 * 頻寬W * 1 = 2 * 頻寬W
如果N=4, 位元率=2 * 頻寬W * 2 = 4 * 頻寬W
如果N=8, 位元率=2 * 頻寬W * 3 = 6 * 頻寬W
如果N=16, 位元率=2 * 頻寬W * 4 = 8 * 頻寬W
如果N=32, 位元率=2 * 頻寬W * 5= 10 * 頻寬W
如果N=64, 位元率=2 * 頻寬W * 6= 12* 頻寬W
如果N=128, 位元率=2 * 頻寬W * 7= 14* 頻寬W
如果N=256, 位元率=2 * 頻寬W * 8= 16* 頻寬W
也就說,在通道頻寬一定的情況,最大的波特率是固定的,即2倍的頻寬。
但可以通過特定的編碼或調變技術,來提升二進位制資料的位元率!!!
第4章 夏農定理
奈奎斯特(Nyquist)準則在理論上,在數學解決了一個重要的問題:
就是理想的無噪聲的通道上,能夠傳送的最大的波特率(或碼元率或符號率)與通道頻寬之間的關係。
然而,理想是豐滿的,現實是殘酷的,顯示的通道,往往都是有噪聲的,根本不存在所謂的理想通道。
那麼噪聲的通道中,最大的波特率(或碼元率或符號率)與通道頻寬之間的關係又是什麼關係呢?
在回答這個問題之前,先要定義和量化噪聲,只有先量化了噪聲,才能確定噪聲對最終傳輸的二進位制位元率的影響。
4.1 噪聲的定義
從生理學觀點來看,凡是干擾人們休息、學習和工作以及人們所要聽的聲音產生干擾的聲音,即不需要的聲音,統稱為噪聲。
從電通訊的角度來看,凡是干擾正常電訊號的其他所有電訊號,統稱為噪聲。

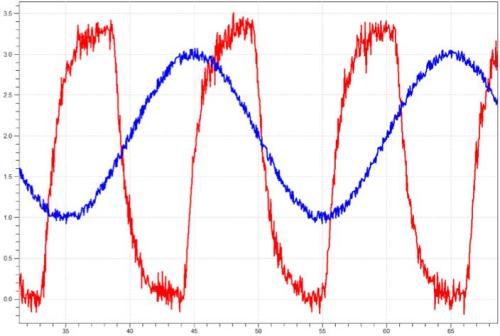
在上圖中,訊號的毛刺就是噪聲造成的,這些噪聲對訊號是乎沒有造成多大的影響。
在下圖中,訊號的毛刺就是噪聲造成的,這些噪聲對訊號就造成了很大的影響。

4.2 訊雜比定義
從上圖可以看出,對於造成對有用訊號的影響,噪聲訊號電平的絕對值是乎意義不大,而採用相對值可以反映噪聲對訊號的影響程度。
在通訊中,採用訊雜比來定義噪聲對訊號的影響程度。
訊雜比,英文名稱叫做SNR或S/N(SIGNAL-NOISE RATIO),又稱為訊噪比。是指一個電子裝置或者電子系統中訊號與噪聲的比值。
這裡面的訊號指的是來自裝置外部需要通過這臺裝置進行處理的電子訊號,
噪聲是指經過該裝置後產生的原訊號中並不存在的無規則的額外訊號(或資訊),並且該種訊號並不隨原訊號的變化而變化。
訊雜比的計量單位是dB,其計算方法是10lg(Ps/Pn),其中Ps和Pn分別代表訊號和噪聲的有效功率,也可以換算成電壓幅值的比率關係:20Lg(Vs/Vn),Vs和Vn分別代表訊號和噪聲電壓的「有效值」。因此,訊雜比應該越高越好。
SNR = 2*10lg(Ps/Pn) = 20lg(S/N)
需要說明的是:
(1)訊雜比並非簡單的線性比,而是先線性比,然後再取對數。
之所以,不是採用簡單的線性比值,主要是因為線性比值的數位太大,表達起來不方便。在通訊系統中,噪聲的能量往往很小,因此Ps/Pn通常都比較大=10^6.
(2)訊雜比 的單位是dB。
如果是簡單的線性比值,是不因該有單位的,而是一個比例值,因為比值後再去對數,於是就有了單位dB
Ps/Pn = 10^0, SNR = 0 = 0dB
Ps/Pn = 10^1, SNR = 2*10 = 20dB
Ps/Pn = 10^2, SNR = 2*20 = 40dB
Ps/Pn = 10^3, SNR = 2*30 = 60dB
Ps/Pn = 10^4, SNR = 2*40 = 80dB
Ps/Pn = 10^5, SNR = 2*50 =100dB
Ps/Pn = 10^6, SNR = 2*60 =120dB
Ps/Pn = 10^7, SNR = 2*70 = 140dB
Ps/Pn = 10^8, SNR = 2*80 =160dB
Ps/Pn = 10^9, SNR = 2*90 =180dB
Ps/Pn = 10^10, SNR = 2*100=200dB

4.3 夏農定理
(1)夏農定理
夏農定理證明:在被高斯白噪聲干擾的通道中,傳送的最大資訊速率C由下述公式確定:
C=W*log₂(1+S/N) (bit/s)
C是資料速率的極限值,單位bit/s;
注意的是:這裡的C不是波特率,而是位元率,已經包含了各種編碼的效率等因素後的綜合結果。
因此,夏農定義預測的是,採用各種技術手段,所能夠達到的最高傳輸速率。
log:2為底的對數
W為通道頻寬,單位Hz;
S是訊號功率(瓦),
N是噪聲功率(瓦)。
夏農公式中的S/N是為訊號與噪聲的功率之比,為無量綱單位。如:S/N=1000(即,訊號功率是噪聲功率的1000倍)
SNR(訊雜比,單位為dB)=10 lg(S/N), 則
S/N=10^(SNR/10),如果SNR=20, S/N=10^(20/10)= 10^2 = 100。
通訊通道的通道容量或夏農限制是指在指定的噪音標準下,通道理論上的最大傳輸率。
可以用夏農公式來計算電話線的資料傳輸速率。
通常音訊電話連線支援的頻寬W=3kHz,而一般鏈路典型的訊雜比是30dB,即S/N=1000,
因此有C=3KHz × log2(1+1000),近似等於30kbps,
假如噪聲值給定,那麼似乎通過增加訊號強度或頻寬就能提高資料率;
但事實並非看起來這邊簡單。主要原因是訊號頻寬W與S/N並非完全獨立的,而是是相關的。
(2) 通過提升訊雜比提升資料傳輸位元率
理想情況下
![]()
但不能無限制的增加訊號的強度來提升資料位元率,因為,如果訊號強度增加了,則系統硬體的非線性程度也會提高,這就導致噪聲的增加,在增加訊號強度的過程中,噪聲的強度也在增加。
因此,訊號強度的提升,功率放大器的線性區間。
假設訊雜比S/N=10^4, 頻寬為W, 則最大的資料傳輸率C= W * Log2(1+10^4) ~= 13W, 也就是頻寬的13倍。
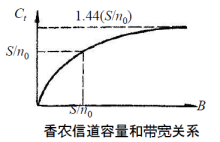
(3) 通過提升頻寬提升資料位元率
不能無限制的增加通道的頻寬來提升資料位元率,頻寬越寬,系統容納的噪聲也就越多,因此隨著B的增加,S/N反而降低了。


第5章 夏農定理與奈奎斯特(Nyquist)準則的關係
奈奎斯特(Nyquist)準則位元率的表示式
C= 2* W*log₂ N(bit/s) = W * log₂ N^2(bit/s)
N是二進位制編碼代表的二進位制的種類, N=2^1, 2^2, 2^3, .....2^8, 2^9, 2^10
N^2 = 2^2, 2^4, 2^6,..... 2^20.....
結論:在頻寬一定的情況下,可以通過提升編碼的效率,提升傳送的位元數。
夏農定理:
C = W * log₂(1+S/N) (bit/s)
S/N是訊雜比。
S/N=10^1, 10^2, 10^3, 10^4.....
結論:在頻寬一定的情況下,可以通過提升編碼的效率,提升傳送的位元數。
於是乎得到一個神奇的結果:
log₂ N^2 ~= log₂(1+S/N)
右邊是有噪聲通道, 右邊是無噪聲的通道。
這就意味著,鏈路的訊雜比與符號的編位元速率之間有著一定的關係!
訊雜比越大,支援的符號的編碼的階數越大,訊雜比越小,噪聲越大,支援的符號的編碼的階數越小。
下表展現了在頻寬一定的情況下,訊雜比與碼元編位元速率的關係:
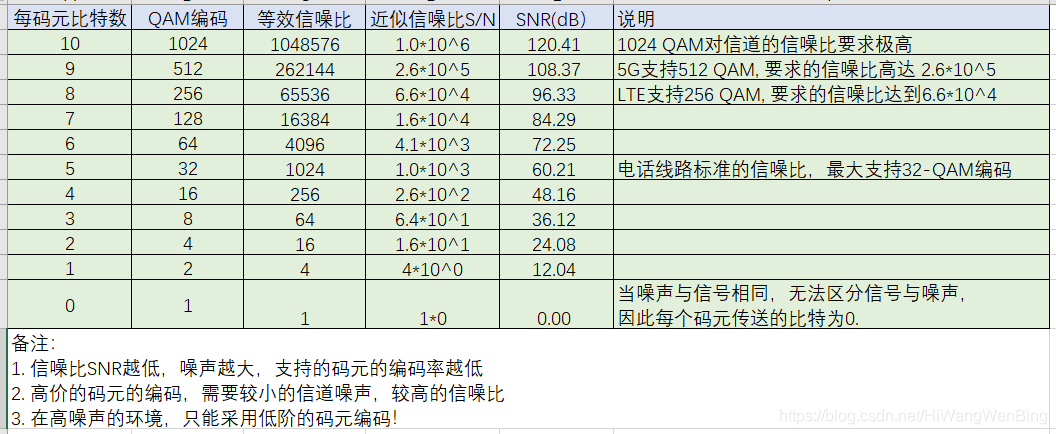
國際電工委員會對訊雜比的最低要求是:
前置放大器大於等於63dB,
合併式放大器大於等於63dB。
後級放大器大於等於86dB,
合併式放大器訊雜比的最佳值應大於90dB,
CD機的訊雜比可達90dB以上,
高檔CD的更可達110dB以上。
參考:
衝激訊號、門訊號、方波、矩形波的傅立葉變換總結: https://zhuanlan.zhihu.com/p/111522114
深入理解奈奎斯特第一準則與碼間串擾: https://blog.csdn.net/weixin_44586473/article/details/104372110
奈奎斯特取樣定理:https://haokan.baidu.com/v?vid=18289428643977245185&pd=bjh&fr=bjhauthor&type=video