NFA到DFA的轉化（保證能講明白）

如何將下圖的NFA轉化為DFA呢？

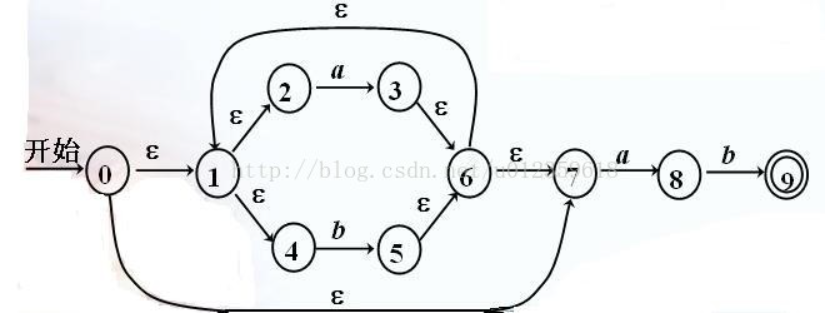
圖1

解答如下:

1. 求出 $\epsilon \_closure(s)$
   $\epsilon \_closure(s)$表示由狀態 $s$ 經由條件 $\epsilon$ 可以到達的所有狀態的集合

ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0)=\{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}
ε _ c l o s u r e ( 1 ) = { 1 , 2 , 4 } ε\_closure(1)=\{1,2,4\} ε_closure(1)={1,2,4}
ε _ c l o s u r e ( 2 ) = { 2 } ε\_closure(2)=\{2\} ε_closure(2)={2}
ε _ c l o s u r e ( 3 ) = { 1 , 2 , 3 , 4 , 6 , 7 } ε\_closure(3)=\{1,2,3,4,6,7\} ε_closure(3)={1,2,3,4,6,7}
ε _ c l o s u r e ( 4 ) = { 4 } ε\_closure(4)=\{4\} ε_closure(4)={4}
ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } ε\_closure(5)=\{1,2,4,5,6,7\} ε_closure(5)={1,2,4,5,6,7}
ε _ c l o s u r e ( 6 ) = { 1 , 2 , 4 , 6 , 7 } ε\_closure(6)=\{1,2,4,6,7\} ε_closure(6)={1,2,4,6,7}
ε _ c l o s u r e ( 7 ) = { 7 } ε\_closure(7)=\{7\} ε_closure(7)={7}
ε _ c l o s u r e ( 8 ) = { 8 } ε\_closure(8)=\{8\} ε_closure(8)={8}
ε _ c l o s u r e ( 9 ) = { 9 } ε\_closure(9)=\{9\} ε_closure(9)={9}

2. 下面的A,B,C…表示一種狀態。如A表示 { 0 , 1 , 2 , 4 , 7 } \{0,1,2,4,7\} {0,1,2,4,7},其實就是$\epsilon \_closure(0)$

為了讀懂下面的內容，在這裡先解釋幾個東西。

1. $\epsilon \_closure(move(A,a))$ 中的 $move(A,a)$是什麼意思呢？
   它代表從狀態A，經過a到達的狀態。
   A狀態是 ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0) = \{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}，在 { 0 , 1 , 2 , 4 , 7 } \{0,1,2,4,7\} {0,1,2,4,7}裡面，對每一個元素都考慮其是否通過a到達了某個狀態，觀察一下圖1，只有狀態2和7經過了a，分別到達了3和8，所以 $move(A,a)$ = { 3 , 8 } \{3,8\} {3,8}，從而有 ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}， { 1 , 2 , 3 , 4 , 6 , 7 , 8 } \{1,2,3,4,6,7,8\} {1,2,3,4,6,7,8}是未出現過的狀態，所以可把它取名為B狀態(其它名字也行).
2. ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} ε_closure({3,8})={1,2,3,4,6,7,8}是怎麼來的呢？
   因為在步驟1我們已經知道， ε _ c l o s u r e ( 3 ) = { 1 , 2 , 3 , 4 , 6 , 7 } ε\_closure(3)=\{1,2,3,4,6,7\} ε_closure(3)={1,2,3,4,6,7}， ε _ c l o s u r e ( 8 ) = { 8 } ε\_closure(8)=\{8\} ε_closure(8)={8} ，然後取它們的並集就得到了 { 1 , 2 , 3 , 4 , 6 , 7 , 8 } \{1,2,3,4,6,7,8\} {1,2,3,4,6,7,8}.
   
   這樣應該解釋明白了。繼續往下看，然後不懂的話再倒回來看看。

ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } = A ε\_closure(0) = \{0,1,2,4,7\} = A ε_closure(0)={0,1,2,4,7}=A
ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( A , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(A,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(A,b))=ε_closure(5)={1,2,4,5,6,7}=C
ε _ c l o s u r e ( m o v e ( B , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(B,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(B,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( B , b ) ) = ε _ c l o s u r e ( { 5 , 9 } ) = { 1 , 2 , 4 , 5 , 6 , 7 , 9 } = D ε\_closure(move(B,b)) = ε\_closure(\{5,9\}) =\{1,2,4,5,6,7,9\} = D ε_closure(move(B,b))=ε_closure({5,9})={1,2,4,5,6,7,9}=D
$\epsilon \_closure(move(C,a))=\epsilon \_closure()$
ε _ c l o s u r e ( m o v e ( C , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(C,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(C,b))=ε_closure(5)={1,2,4,5,6,7}=C
ε _ c l o s u r e ( m o v e ( D , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(D,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(D,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( D , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(D,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(D,b))=ε_closure(5)={1,2,4,5,6,7}=C

3. 畫出DFA狀態轉換表
   步驟2中有A,B,C,D四種情況，其中A是初始情況（ ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0)=\{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}. 多說幾句，在NFA圖1中，是從0出發的，所以初始情況是$\epsilon \_closure(0)$，那假設如果是從X開始，則初始情況是$\epsilon \_closure(X)$）

看步驟2， ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B，所以A行a列填B，其他同理。

	a	b
A	B	C
B	B	D
C	B	C
D	B	C

4. 根據DFA狀態轉換表畫出DFA狀態轉換圖

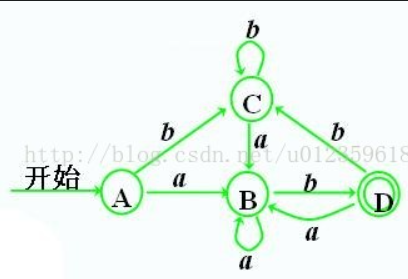
看步驟3的表格，A經過a到B，A經過b到C，B經過a到B，以此類推…

參考：
NFA到DFA的轉化🔗